Disassortative Degree Mixing and Information Diffusion for Overlapping Community Detection in Social Networks

Christian Hoyer	Marc Osterberg	Cedrik Albrecht	Julian Düstersiek
RWTH Aachen	RWTH Aachen	RWTH Aachen	RWTH Aachen
Christian.Hoyer@rwth-aachen.de	Marc.Osterberg@rwth-aachen.de	Cedrik.Albrecht@rwth-aachen.de	Julian.Duestersiek@rwth-aachen.de

In der heutigen Zeit gewinnen soziale Netzwerke immer mehr an Bedeutung, weshalb es zunehmend wichtiger wird, bestimmte Gruppierungen in diesen ermitteln zu können. Daher wollen wir in dieser Publikation einen Algorithmus zur Ermittlung solcher Gruppierungen vorstellen. Der Algorithmus operiert in zwei Phasen auf einer disassortativen Matrix, die das Netzwerk repräsentiert. In der ersten Phase untersucht man den Grad jedes Knotens und vergleicht ihn mit den Graden in seiner Umgebung, dabei ergeben sich die Anführer des Netzwerks. In der zweiten Phase wird anschließend berechnet, wie stark die Anführer die anderen Knoten im Netzwerk beeinflussen und ob diese ihre Eigenschaften übernehmen. Dadurch ergibt sich eine präzise Darstellung der Gruppierungen in realitätsnahen Netzwerken, welche in einer, im Vergleich mit anderen Algorithmen, guten Laufzeit erreicht wurde und somit auch auf sehr großen Netzwerken anwendbar ist. So macht den vorgestellten Algorithmus die Aufdeckung von hierarchischen Strukturen und die Berechnung der Beeinflussung der Knoten untereinander konkurrenzfähig gegenüber anderen „Overlapping Community Detection“-Algorithmen.

1. Einleitung

In jedem sozialen Netzwerk gibt es eine Vielzahl an Communitys, innerhalb derer Individuen mit gemeinsamen Zielen oder Interessen miteinander interagieren. In den vergangenen Jahren sind Communitys vermehrt in den Fokus der Forschung geraten. Die ersten Algorithmen zu deren Entdeckung waren dafür gedacht, eine Menge von disjunkten Communitys zu bestimmen. Die Nutzerzahlen von sozialen Netzwerken sind in letzter Zeit stark angestiegen und auch für die Zukunft wird ein Wachstum prognostiziert. Dadurch erhöht sich nicht nur stetig die Anzahl der Communitys, sondern es kommt auch zu einer immer stärker werdenden Überlappung verschiedener Communitys, da die meisten Nutzer Teil von mehreren Communitys gleichzeitig sind. In Folge dessen hat die “overlapping community detection” kürzlich viel Aufmerksamkeit auf sich gezogen (Jin et al., 2011),(Evans, 2010),(Evans & Lambiotte, 2010),(Havemann et al., 2011),(Fan et al., 2012),(Huang et al., 2011),(Li et al., 2012),(Wu et al., 2012),(Xie et al., 2011).

Mittlerweile gibt es eine Vielzahl von Methoden, um solche “overlapping communities” zu identifizieren. Eine Kategorie, für welche die Modularitätsoptimierung von Girvan und Newman ein typisches Beispiel ist, nutzt globale Eigenschaften des Graphen wie den “global clustering coefficient” oder Modularitätswerte, um ein zum Graph passendes Cover zu erstellen. Die andere Kategorie besteht aus sogenannten lokalen Methoden, welche die bei globalen Methoden auftretenden Probleme wie Auflösungsgrenze oder Zeitkomplexität mit Hilfe von Optimierungstechniken und lokalen Dynamiken umgehen (Jin et al., 2011),(Stanoev et al., 2011),(Xie et al., 2013),(Xie et al., 2011),(Gregory, 2010),(Gregory, 2008),(Chen et al., 2009),(Xie et al., 2011). Ein Teil dieser lokaler Methoden konzentriert sich dabei auf die Identifizierung der einflussreichsten Knoten, da sich Communitys oftmals um diese herum formen (Stanoev et al., 2011). Die Identifizierung geschieht dabei mit Hilfe verschiedener Prozesse und Metriken wie Knotengewicht/-grad (Chen et al., 2009),(Jin et al., 2011), Knotendistanzen (Li et al., 2012) oder “random walks” (Stanoev et al., 2011). Diese einflussreichsten Knoten, auch als “Anführer” bezeichnet, werden dann einzeln oder in Gruppen als Community betrachtet. Darauf aufbauend werden im Anschluss die Zugehörigkeiten der anderen Knoten des Graphen bestimmt.

Eine solche lokale Methode, die sich auf die Identifizierung der Anführer konzentriert, wollen wir in dieser Arbeit vorstellen. Es handelt sich um “Disassortative Degree Mixing and Information Diffusion for Overlapping Community Detection in Social Networks” (Abk.: DMID). Es ist ein Algorithmus, der im Jahr 2015 erschienen und somit zum Zeitpunkt der Veröffentlichung dieser Arbeit ziemlich neu ist. Er benutzt nacheinander zwei verschiedene Dynamiken, um Communitys zu identifizieren: “disassortative degree mixing” und “information diffusion”. “Disassortative mixing” bezeichnet dabei die Tendenz eines Knotens, hauptsächlich mit Knoten in Verbindung zu stehen, die einen Rang/Grad einer anderen Größenordnung besitzen. Ein disassortativer Knoten mit einem hohen Rang/Grad kommuniziert also vorwiegend mit niedrigrangigen/-gradigen Knoten und umgekehrt. Diese Art von Beziehung findet sich in vielen Communitys in sozialen Netzwerken wieder und trifft somit auch auf die Beziehung der Anführer und ihrer Nachbarknoten zu. Um Communitys zu identifizieren ist es deshalb notwendig, nach “disassortative hubs” zu suchen, wofür es eine Vielzahl von Vorgehensweisen gibt. DMID setzt auf einen “random walk” Prozess, der im Kapitel 3 genauer erklärt wird. In der zweiten Phase des Algorithmus wird die Beziehung von jedem Knoten zu den Communitys bestimmt. Dies geschieht mit Hilfe des sogenannten “network coordination game”, das auf den Dynamiken der “information diffusion” basiert. Dieser Prozess wird ebenfalls im Kapitel 3 detailliert beschrieben.

2. Verwandte Arbeiten

Da diese Arbeit den bereits existierenden DMID Algorithmus vorstellt, basiert sie an vielen Stellen auf den Ergebnissen des Originalartikels “Disassortative Degree Mixing and Information Diffusion for Overlapping Community Detection in Social Networks” von Shahriari, Krott und Klamma (Shahriari et al., 2015). Dies betrifft vor allem das nächste Kapitel. Desweiteren wird der DMID Algorithmus neben fünf anderen OCD Algorithmen auf einer Java-basierten Peer-to-Peer Infrastruktur getestet, die ebenfalls ein Resultat des Originalartikels ist. Bei den anderen fünf Algorithmen handelt es sich um SSK(Stanoev et al., 2011), CLiZZ (Li et al., 2012), MONC (Havemann et al., 2011), LC (Xie et al., 2013) und SLPA, die von anderen Teams des Seminars, in dessen Rahmen diese wissenschaftliche Arbeit entsteht, behandelt werden. Um DMID in Relation zu diesen Algorithmen zu bringen und um somit auch Rückschlüsse auf DMIDs Leistung ziehen zu können, werden deshalb alle Algorithmen auf der Peer-to-Peer Infrastruktur getestet. Die Ergebnisse dieses Tests zeigen, dass DMID sowohl in der Präzision als auch in der Zeitkomplexität konkurrenzfähig ist.

3. Funktionsweise

3.1 Verwendete Terme und Variablen

Das soziale Netzwerk, welches wir auf Communitys untersuchen wollen, stellen wir als Graphen \(G=(V,E)\) dar. Die Menge \(V\) enthält alle Knoten, welche in unserem Modell für die Nutzer des sozialen Netzwerks stehen, und die Menge aller Kanten \(E\) enthält die Beziehungen zwischen den Benutzern. Zudem ist die Gesamtanzahl aller Knoten \(n\) = \(|V|\) und die Anzahl aller Kanten \(m\) = \(|E|\). Wir bezeichnen den Knoten \(j\) als Nachbarn zum Knoten \(i\), wenn diese adjazent, also über eine Kante miteinander verbunden, sind. Die Menge \(N(i)\) enthält alle Nachbarsknoten des Knotens \(i\) und \(deg(i)\) bezeichnet die Anzahl aller Kanten an \(i\).
Die vorhandene Struktur der Communitys stellen wir als Tupel \(\Gamma\) = (\(C_{1}\),\(C_{2}\),…,\(C_{h}\)) dar. \(h\) ist demnach die Anzahl aller Communitys |\(\Gamma\)|. Der Eintrag \(M_{ij}\) der Mitgliedschaftsmatrix \(M\) gibt an, inwiefern \(i\) ein Teil der Community \(C_{j}\) ist.

3.2 Identifizierung der Anführer

Um die Anführer des Netzwerks ausfindig zu machen, nutzen wir den “Disassortative Random Walk”. Wir bezeichnen solche Knoten als stark vernetzt, die einen hohen Grad haben. Wenn im Netzwerk Knoten hohen Grades hauptsächlich mit Knoten mit geringen Grades über Kanten verbunden sind, so bezeichnen wir das Netzwerk als disassortativ. Ein einzelner Knoten ist folglich genau dann disassortativ, wenn sein Grad stark vom Grad der meisten Nachbarknoten abweicht. Einen disassortativen und stark vernetzten Knoten bezeichnet man als Anführer. Ein solcher Anführer zeichnet sich dadurch aus, dass er mit deutlich mehr Knoten in Kontakt steht, als die Knoten in seiner direkten Umgebung.
Zu Beginn definieren wir die disassortative Matrix mit Einträgen, welche den Unterschied im Grad der zugehörigen Knoten darstellen.

\[AS_{ij}=|deg(i)-deg(j)|\]

Wir müssen diese Matrix in eine nach Zeilen normalisierte Form bringen, bevor wir den “Random Walk” anwenden können. Dafür teilen wir jeden Eintrag durch die Summe aller Werte in dieser Zeile.

\[T_{ij}=\frac{AS_{ij}}{\sum_{k=1}^{deg(i)} AS_{ik}}\]

Nun definieren wir einen Vektor \(DA\), dessen Eintrag an der \(i\)-ten Stelle uns später die Disassortativität des Knotens \(i\) liefern soll. Zum Startzeitpunkt belegen wir die Werte des Vektors jeweils abhängig vom Grad des zugehörigen Knotens.

\[DA_{i}^{0}=\frac{1}{deg(i)}\]

Der “Random Walk” ist die mathematische Modellierung von einem zufallsbasierten Lauf durch \(G\), dabei liefert \(DA\) die Wahrscheinlichkeiten in welchem Knoten wir uns befinden und \(T\) die Wahrscheinlichkeiten in welchen Knoten wir wechseln. Bei der Ausführung des “Random Walk” haben Kanten, die zwei disassortative Knoten verbinden, aufgrund der Beschaffenheit von \(T\) eine höhere Wahrscheinlichkeit gewählt zu werden. Es ergibt sich somit ein proportionales Verhältnis zwischen der Wahrscheinlichkeit der Kante gewählt zu werden und dem Grad an Disassortativität des Knotens, den man über die Kante erreicht. Somit erhalten wir einen Vektor \(DA^{t}\), der die Disassortativität nach \(t\) Wiederholungen angibt.

\[DA^{t+1}=DA^{t} \times T\]

Dieses Verfahren führt zu einem Fixvektor \(DA_{i}^{t^*}\) nach einer endlichen Anzahl an Schritten \(t^*\). Dieser gibt uns die lokale Disassortativität des Knotens \(i\) an. Wir fahren mit der Suche nach Anführern fort, indem wir einen normalisierten Vektor für den Grad der Knoten berechnen.

\[DRN_{i}= \frac{deg(i)}{\max_{k \in V} deg(k)}\]

Indem wir den Grad des Knotens mit dem Wert für Disassortativität kombinieren, erhalten wir einen Wert für das Potential als Anführer.

\[LS_{i}=DA_{i} \times DRN_{i}\]

Ein lokaler Anfüher soll ein Knoten sein, der ein höheres Anführerpotential als alle seine Nachbarsknoten hat. Der Knoten \(i\) wird somit zu einem lokalen Anführer, wenn für alle \(j\) \(\in\) \(N(i)\) gilt

\[LS_{i}>LS_{j}\]

Die Menge aller lokalen Anführer bezeichnen wir mit \(LL\) und die Knoten, die mit ihnen verbunden sind, als ihre Anhänger. Die Menge der Anhänger eines Knotens \(i\) ist \(FL(i)\). Die Anzahl dieser Anhänger eines jeden lokalen Anführers werden miteinander verglichen um die einflussreichsten Anführer zu finden. Dafür bestimmen wir die durchschnittliche Anzahl an Anhängern mit

\[AFD=\frac{\sum_{i\in LL} |FL(i)|}{|LL|}\]

Ein globaler Anführer definiert sich durch die überdurchschnittliche Anzahl an Anhängern.

\[|FL(i)| > AFD\]

3.3 Einflüsse auf das Netzwerk

Neben den globalen Anführern, welche die Mittelpunkte unserer Communitys markieren, gilt es herauszufinden, in welchem Maß die Knoten in den verschiedenen Communitys beteiligt sind. Um dies zu bestimmen, nutzen wir ein “Cascading Behaviour” als “Network Coordination Game”. Dafür ist es wichtig, wie lange ein Knoten \(i\) braucht, um das Verhalten eines Anführers zu übernehmen. Dafür wenden wir das “Network Coordination Game” auf jeden Anführerknoten an. Der Anführer \(L_{j}\) startet mit einem Verhalten \(A\), welches keiner der anderen Knoten aufweist. In jedem Durchlauf werden Knoten das Verhalten \(A\) übernehmen, wenn der Anreiz \(p_{A}\) größer ist als die Schwelle in der aktuellen Runde. Wir definieren

\[p_{A}(i)=\frac{|\{j \in N(i)|j \; hat \; Verhalten \; A\}|}{deg(i)}\]

und unseren Schwellenwert als den Durchschnitt von zwei Grenzen, welche wir mit 0 und 1 initialisieren. Da der Durchschnitt mit einer binären Suche zwischen den Grenzen ermittelt wird, muss vorher festgelegt worden sein, wie genau dies geschieht. Nach jedem Durchlauf wird die obere Grenze gesenkt, wenn alle Knoten mindestens ein Verhalten übernommen haben. Ist dies nicht der Fall, so wird die untere Grenze erhöht. Nimmt ein Knoten \(i\) also nach \(t\) Durchläufen ein bestimmtes Verhalten \(A\) an, welches vom Anführer \(L_{j}\) ausging, so ist er zu einem gewissen Grad Teil der zugehörigen Community \(C_{j}\). Der genaue Grad der Mitgliedschaft ist in der Matrix \(M\) mit

\[M_{ij}=\frac{1}{t_{i}^2}\]

angegeben. Das Spiel endet, wenn in einem Durchlauf kein Knoten mehr ein neues Verhalten übernommen hat. Somit erhalten wir nach endlich vielen Schritten die Matrix \(M\), welche uns nicht nur die Communitys sondern auch den Grad der Mitgliedschaft der einzelnen Knoten zeigt.

3.4 Veränderungen bei gerichteten Graphen und Laufzeitanalyse

Wollen wir statt eines Netzwerks mit ungerichteten Kanten, eines mit gerichteten Kanten untersuchen, so muss nicht viel geändert werden. Im ersten Abschnitt bei der Identifizierung der Anführer nutzen wir statt des Grads eines Knotens \(deg(i)\) seinen Eingangsgrad \(deg^-(i)\), also die Anzahl der Knoten, deren Nachfolger \(i\) ist. Im zweiten Abschnitt verändert sich lediglich die Berechnung des Wertes für den Anreiz.

\[p_{A}(i)=\frac{|\{j \in N(i)|j \; hat \; Verhalten \; A\}|}{deg^+(i)}\]

Wobei \(deg^+(i)\) die Anzahl der Nachfolger von \(i\) ist. Unter dem Vorbehalt, dass jeder Knoten Mitglied in einer konstanten Anzahl an Communitys ist und alle Communitys etwa gleich groß sind, so liegt die Zeitkomplexität in \(O(m\frac{n}{h})\).

4. Anwendung

In diesem Abschnitt werden die Resultate mehrerer Anwendungen von DMID auf verschiedenen Netzwerken dargestellt. Dabei werden sowohl synthetische als auch reale Netzwerke verwendet. Abschließend wird DMID mit anderen OCD-Algorithmen, wie bspw. Clizz oder SSK, verglichen und bewertet.

4.1 Leistung auf verschiedenen Datensätzen

Die verwendeten synthetischen Netzwerke wurden durch LFR (Lancichinetti & Fortunato, 2009) mit angegebenen Parametern erzeugt. Um die Algorithmen angemessen miteinander zu vergleichen, wurden die jeweiligen NMI- und Modularitätswerte ermittelt. NMI steht für “normalized mutual information” und wird benutzt um die Ähnlichkeit zweier Datensätze zu bestimmen. Dabei bedeutet der Wert 1, dass die beiden Datensätze identisch sind und 0, dass sie keine Schnittmenge besitzen.(Strehl & Ghosh, 2002) Dieser metrische Wert wird meist nur bei synthetischen Netzwerken ermittelt, da dort ein genauer Wahrheitswert für einen Vergleich bekannt ist und somit der Algorithmus auf seine Richtigkeit, bspw. bezüglich Ermittlung der Communitys, geprüft werden kann. Ein positiver Modularitätswert hingegen deutet auf eine Struktur ähnlich einer Community im Datensatz hin (ein negativer Wert deutet auf die Abwesenheit solcher Strukturen hin)(Newman, 2004) und kann deshalb auch auf realen Netzwerken angewandt werden.

4.2 Vergleich mit anderen OCD-Algorithmen

a) Zachary Karate Club

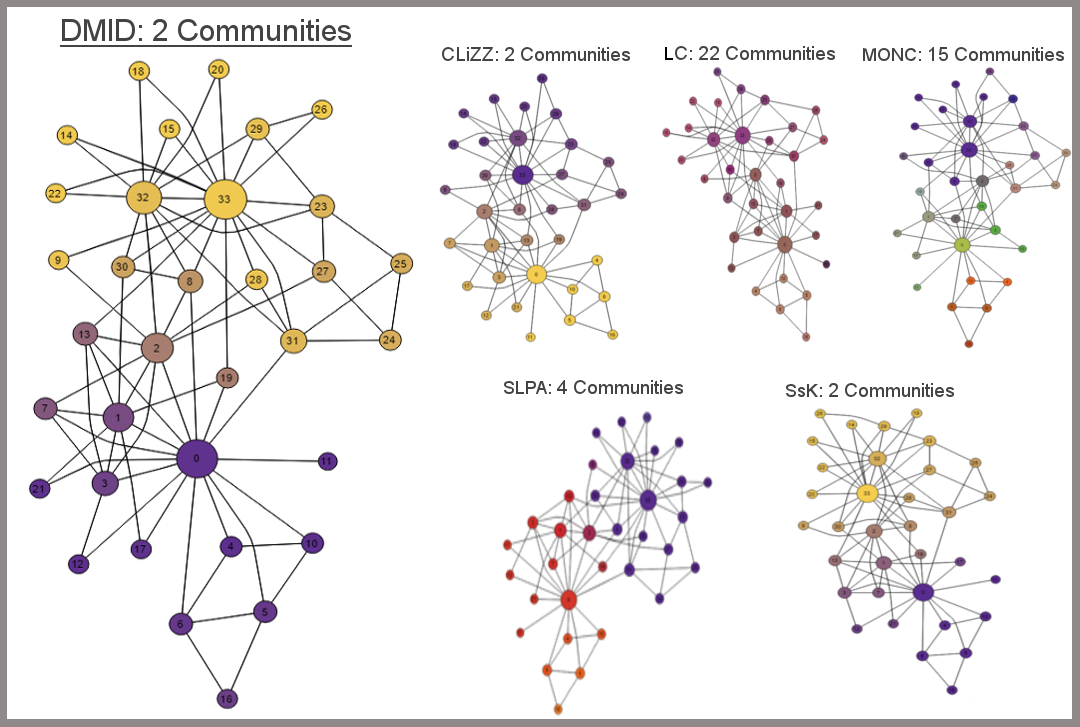
Zachary Karate Club (Zachary, 1977) ist einer der populärsten Datensätze um Algorithmen für Community-Entdeckung zu testen. Dieses Netzwerk besteht aus 34 Knoten, die Mitglieder eines Karateclubs, und 78 Kanten, welche für die Freundschaften untereinander stehen. Laut dem Autor besitzt Zachary Karate Club zwei Communitys, die Freunde des Trainers und die Freunde des Clubsprechers, und soll einen Konflikt zwischen Trainer und Sprecher des Clubs darstellen. DMID war in der Lage diese Communitys mit deren Anführern (0, 33) korrekt zu identifizieren, ebenso wie die Knoten, die beiden Communitys angehören (8, 30, 13, 2, 1, 19). Bis auf die Zugehörigkeit der Knoten 2 und 19 hat DMID den Graph korrekt interpretiert.

b) Reale Netzwerke

Hier wurde DMID auf zwei verschiedenen realen Netzwerken mit jeweils ca. 4000 Knoten angewandt; einem sozialen und einem technischen Netzwerk. Das erste Netzwerk ist ein anonymisierter Ausschnitt aus Facebook mit 176468 Kanten. Hier erzielt DMID einen durchschnittlich guten Modularitätswert innerhalb einer moderaten Zeit im Vergleich zu CLiZZ und SSK. Das zweite Netzwerk ist ein technisches und stellt den Teil eines Stromnetzes aus dem Westend der USA dar. Bei der Anwendung auf dieses Netzwerk erzielt DMID innerhalb einer vergleichsweisen guten Laufzeit einen sehr hohen Modularitätswert.

c) Durchschnittlich große synthetische Netzwerke

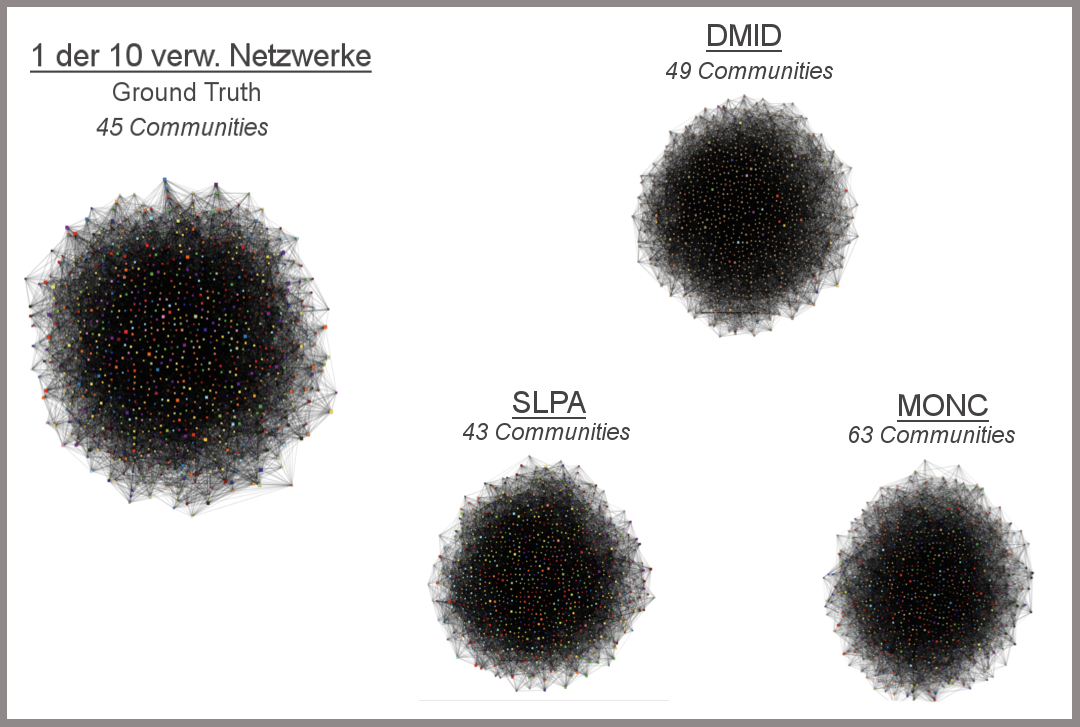
Um die Leistung DMID’s im Vergleich zu anderen Algorithmen auf synthetischen Netzwerken zu testen, wurden 10 Netzwerke mit gleichen Parametern durch LFR erzeugt. Die hier dargestellten Werte sind Durchschnittswerte aus den Ergebnissen, die die Algorithmen auf diesen 10 Netzwerken lieferten. Die Parameter wurden dabei nicht optimal für DMID gewählt, um zudem die Robustheit des Algorithmus zu testen (Maximaler und durchschnittlicher Knotengrad liegen nah beieinander, jeder vierte Knoten ist nicht in mehreren Communitys und die Communitys sind nicht sehr groß). Im Vergleich zu den anderen Algorithmen, erzielt DMID hier den höchsten NMI-Wert innerhalb der kürzesten Laufzeit, d.h. DMID’s Interpretation des Netzwerks ähnelt dem tatsächlichen am meisten. LC ist nicht in einer angebrachten Laufzeit terminiert und die durchschnittliche Laufzeit von SSK war zu hoch um im Diagramm dargestellt zu werden.

4.3 Bewertung

An den Ergebnissen dieser Stichproben lässt sich erkennen, dass DMID einen sehr kompetitiven Algorithmus darstellt. Auf kleinen Netzwerken liefert er nahezu komplett korrekte Datensätze, selbst bei untypischen Netzwerken durchschnittlicher Größe mit niedrigem Modularitätswert ist er in der Lage, Communitys innerhalb einer guten Laufzeit zu ermitteln und zudem findet er nicht nur Anwendung bei großen Datensätzen sozialer Netzwerke, sondern kann auch für Netzwerke mit einem anderen Anwendungsgebiet benutzt werden (bpsw. bei technischen Netzwerken). Außerdem bietet DMID den Vorteil, dass lokale und globale Anführer unterschieden werden und somit Knoten in eine Hierachie eingeteilt werden können.

5. Zusammenfassung und Ausblick

In dieser wissenschaftlichen Arbeit haben wir den zwei-Phasen Algorithmus DMID zur Entdeckung von Communitys in sozialen Netzwerken mit „disassortative degree mixing“ und „information diffusion“ vorgestellt, welcher sich durch einige Vorteile gegenüber anderen „Overlapping Community Detection“-Algorithmen hervorhebt. Es werden Anführer als „disassortive hubs“ identifiziert, mit deren Grundlage sich das Entdecken von Communities in Netzwerken verbessert. Eine weitere Eigenschaft ist die Offenlegung von hierarchischen Strukturen in Netzwerken, die erkennen lassen, welcher Knoten höher als andere gestellt und somit auch bedeutsamer ist. So lässt sich durch die Identifizierung von überlappenden Knoten die Wahrscheinlichkeit der Zugehörigkeit zu jedem anderen Knoten im Netzwerk bestimmen und auch mit welcher Wahrscheinlichkeit ein Knoten das Verhalten eines anderen übernehmen wird. Für zukünftige Arbeiten wird die Untersuchung der Auswirkung von Netzwerken mit verschiedenen assortativen Werten bedeutsam. Also wann genau sich das Verhalten in Netzwerken ändert, in denen nur ein Anführer existiert und alle anderen Knoten denselben Schwellenwert haben. Außerdem ließe sich der Algorithmus so erweitern, dass in der ersten Phase mehrere Anführer für jede Communitie zugelassen wären und in der zweiten Phase verschiedene Schwellenwerte für die anderen Knoten möglich wären. Im Hinblick auf die Zeitkomplexität ist es ein großer Vorteil, dass nur auf lokale Informationen zugegriffen wird und der Algorithmus somit in dezentralen Umgebungen eingesetzt werden kann. Ein weiterer Aspekt der zukünftigen Arbeit wird deshalb die Implementierung des „Map-Reduce framework“ und das Ausführen auf sehr großen Netzwerken sein.

6. Referenzen

1. Jin, D., Yang, B., Baquero, C., Liu, D., He, D., & Liu, J. (2011). A Markov random walk under constraint for discovering overlapping communities in complex networks. Journal of Statistical Mechanics: Theory and Experiment, 2011(05), P05031.
2. Evans, T. S. (2010). Clique graphs and overlapping communities. Journal of Statistical Mechanics: Theory and Experiment, 2010(12), P12037.
3. Evans, T. S., & Lambiotte, R. (2010). Line graphs of weighted networks for overlapping communities. The European Physical Journal B-Condensed Matter and Complex Systems, 77(2), 265–272.
4. Havemann, F., Heinz, M., Struck, A., & Gläser, J. (2011). Identification of overlapping communities and their hierarchy by locally calculating community-changing resolution levels. Journal of Statistical Mechanics: Theory and Experiment, 2011(01), P01023.
5. Fan, M., Wong, K. C., Ryu, T., Ravasi, T., & Gao, X. (2012). SECOM: A Novel Hash Seed and Community Detection Based-Approach for Genome-Scale Protein.
6. Huang, J., Sun, H., Han, J., & Feng, B. (2011). Density-based shrinkage for revealing hierarchical and overlapping community structure in networks. Physica A: Statistical Mechanics and Its Applications, 390(11), 2160–2171.
7. Li, H.-J., Zhang, J., Liu, Z.-P., Chen, L., & Zhang, X.-S. (2012). Identifying overlapping communities in social networks using multi-scale local information expansion. The European Physical Journal B-Condensed Matter and Complex Systems, 85(6), 1–9.
8. Wu, Z., Lin, Y., Wan, H., Tian, S., & Hu, K. (2012). Efficient overlapping community detection in huge real-world networks. Physica A: Statistical Mechanics and Its Applications, 391(7), 2475–2490.
9. Xie, J., Szymanski, B. K., & Liu, X. (2011). Slpa: Uncovering overlapping communities in social networks via a speaker-listener interaction dynamic process. Data Mining Workshops (ICDMW), 2011 IEEE 11th International Conference On, 344–349.
10. Stanoev, A., Smilkov, D., & Kocarev, L. (2011). Identifying communities by influence dynamics in social networks. Physical Review E, 84(4), 046102.
11. Xie, J., Kelley, S., & Szymanski, B. K. (2013). Overlapping community detection in networks: The state-of-the-art and comparative study. Acm Computing Surveys (Csur), 45(4), 1–35.
12. Gregory, S. (2010). Finding overlapping communities in networks by label propagation. New Journal of Physics, 12(10), 103018.
13. Gregory, S. (2008). A fast algorithm to find overlapping communities in networks. Joint European Conference on Machine Learning and Knowledge Discovery in Databases, 408–423.
14. Chen, D., Fu, Y., & Shang, M. (2009). An efficient algorithm for overlapping community detection in complex networks. 2009 WRI Global Congress on Intelligent Systems, 1, 244–247.
15. Shahriari, M., Krott, S., & Klamma, R. (2015). Disassortative degree mixing and information diffusion for overlapping community detection in social networks (dmid). Proceedings of the 24th International Conference on World Wide Web, 1369–1374.
16. Lancichinetti, A., & Fortunato, S. (2009). Benchmarks for testing community detection algorithms on directed and weighted graphs with overlapping communities. Physical Review E, 80(1), 016118.
17. Strehl, A., & Ghosh, J. (2002). Cluster ensembles—a knowledge reuse framework for combining multiple partitions. Journal of Machine Learning Research, 3(Dec), 583–617.
18. Newman, M. E. J. (2004). Fast algorithm for detecting community structure in networks. Physical Review E, 69(6), 066133.
19. Zachary, W. W. (1977). An information flow model for conflict and fission in small groups. Journal of Anthropological Research, 33(4), 452–473.