Adaption traditioneller OCDA für Multilayer-Netzwerke
| Okan Dag |
|---|
| RWTH Aachen University |
| okan.dag@rwth-aachen.de |
| Hakan Hökelekli |
|---|
| RWTH Aachen University |
| Hakan.Hoekelekli@rwth-aachen.de |
Abstract
Durch das System der Massenkommunikation und das Netzwerk interpersonaler Kommunikation, ist die Gesellschaft viel stärker miteinander vernetzt als je zuvor. Anhand von Informationen und Datensätzen erhält man Netzwerke, in welchen anhand von passenden OCD (Overlapping Community Detection) - Algorithmen spezifische Communities gefunden werden können. Diese spiegeln wiederum jegliche sozialen Gruppen unserer Gesellschaft wider. Dazu gehören Daten wie Freunde bei Facebook, Follower auf Instagram oder Chatgruppen auf Whatsapp. Informationen, Daten und Kommunikationen in diversen Plattformen liefern ein perfektes Beispiel für die Nutzung von Multilayer-Netzwerken. Da es bereits viele gut funktionierende OCDAs gibt, stellt sich die Frage, ob sich diese so adaptieren lassen, dass sie auch auf Multilayer Netzwerken anwendbar sind. Diese Thematik, sowie die Abwägung unserer Methoden hinsichtlich einer gut gelungenen Adaption werden im Folgenden diskutiert und damit auch beleuchtet, ob dies sinnvolle Ansätze sind.
Das Problem besteht unter anderem bei den Adaptionsmethoden, da diese über keine allzu tiefgreifenden bzw. geringen Ausarbeitungen der Ansätze verfügen und keine präzise Zahl an Multilayer-Algortihmen existiert (was eine intensive Analyse dieser deutlich erschwert), als auch bei den Surveys dieser Methoden, da diese nicht nur strukturelle Probleme aufweisen, sondern auch nur eine mangelnde oder kaum zufriedenstellende Übersicht bieten.
Ziel unserer Arbeit ist es unteranderem abschließend in einen Konsens darüber zu gelangen, ob es ein guter Ansatz ist traditionelle OCDA in Multilayer-Netzwerke zu überführen, durch welchen wir hinweg wissenschaftliche Arbeiten und Literaturen über unser Thema elaborieren welche den Leser*innen eine möglichst weite Auskunft geben soll, sodass dieser in der Lage ist dementsprechend seine eigene Meinung zu bilden.
Inhaltsverzeichnis
1. Einleitung
Auf wissenschaftlicher Ebene erlangen komplexe Netzwerke einen Zuwachs an Aufmerksamkeit, was auch auf die Verfügbarkeit umfangreicher Netzdaten aus verschiedenen Bereichen und den Ausbruch neuartiger Analyseparadigmen zurückzuführen ist, die Beziehungen und Verbindungen zwischen Entitäten oder Personen in den Mittelpunkt der Untersuchung stellen. (“Foundations of Multidimensional Network Analysis,” 2011) In unserem Paper befassen wir uns mit der Adaption traditioneller OCDA für Multilayer-Netzwerke. OCDA, auch ein Akronym für „Overlapping Community Detection Algorithms“ bieten eine umfassende Analyse von diversen Kollektiven, die mit anderen -nicht zwingend gleichinteressierten- Communities in Verbindung stehen. Diese Verbindungen werden anhand von Knoten dargestellt, mit welchen sich durch Kanten die verschiedene Beziehungen visualisieren lassen, die sowohl innerhalb einer Community hervortreten, allerdings auch Community-Übergreifend existieren können.
Die meisten der bisher untersuchten Netze sind eindimensional: Es kann nur eine Verbindung zwischen zwei Knoten geben. In diesem Zusammenhang hat sich die Netzwerkanalyse auf die Charakterisierung und Messung lokaler und globaler Eigenschaften solcher Graphen konzentriert, wie z. B. Durchmesser, Gradverteilung, Zentralität, Konnektivität - bis hin zu anspruchsvolleren Entdeckungen auf der Grundlage von Graph Mining, die darauf abzielen, häufige Teilgraphenmuster zu finden und die zeitliche Entwicklung eines Netzwerks zu analysieren (“Foundations of Multidimensional Network Analysis,” 2011).
Sogenannte „Multilayer-Netzwerke“ stellen hauptsächliche soziale Netzwerke dar, welche von einer immensen Anzahl an Individuen alltäglich auf Plattformen für die Kommunikation verwendet wird. Multilayer-Netzwerke tragen zur Forschung von Netzwerken bei, indem diese einen Ansatz für die Definition epidemiologischer relevanter Gruppen interagierender Knoten bietet (Kinsley AC & K, 2020).
In unserem Paper wird exemplarisch auf die Community Erkennung in solchen besonderen vielschichtigen Netzwerken eingeganen.
Dementsprechend befasst sich unser Thema mit bereits bestehenden Algorithmen für die „Community Detection“ und die Frage wie sich diese auf die Verknüpfungen verschiedener Nutzer -sowohl innerhalb einer Community als auch extern- in Multilayer-Netzwerken anwenden lassen.
In unserem Paper soll das bereits im Abstract erwähnte Problem aufgegriffen und angegangen werden, sodass es zu einer geordneten Darbietung von Algorithmen und Methoden kommt, um dem Leser eine massenreiche Auskunft über die jeweiligen Ansätze der Adaption zu vermitteln, sodass ein Voranschreiten bezüglich dieses Themas in der wissenschaftlichen Forschung ermöglicht wird.
2. Verwandte Arbeiten
Zu verwandten Arbeiten unseres Thema zählen u.a. das Paper „A survey of community detection methods in multilayer networks“ von Xinyu Huang, Dongming Chen, Tao Ren und Dongqi Wang, dieses Paper bietet einen allgemeinen Vergleich bestehender Arbeiten und es werden mehrere verschiedene repräsentative Algorithmen analysiert, um ein umfassendes Verständnis von Erkennungsmethoden in mehrschichtigen Netzen zu vermitteln. Auch das Paper „Community Detection and Improved Detectability in Multiplex Networks“ von Yuming Huang, Ashkan Panahi, Member, Hamid Krim, Fellow, und Liyi Dai, Fellow wird verwendet, da dieses das weit verbreitete Problem der Erkennung von Gemeinschaften in multiplexen Netzwerken, wie z. B. sozialen Netzwerken, mit einer unbekannten, willkürlichen heterogenen Struktur ausführlich untersucht, was für unser Paper auch sehr ausschlaggebend ist. Außerdem hilft das Paper „Neural Nonnegative Matrix Factorization For Hierarchical Multilayer Topic Modeling“ und „Label propagation algorithm: A semi-synchronous approach“ zum Verständnis von Algorithmen zur Entdeckung von Multilayer-Netzwerken. Von dem wohl zu unserem Thema verwandteste Paper „Finding overlapping communities in multilayer networks” von Weiyi Liu, Toyotaro Suzumura, Hongyu Ji und Guangmin Hu wird auch zum kleinen Teil Gebrauch gemacht, da dieses eine wichtige Methode zur Community Detection in Multilayer-Netzwerken bietet, und zwar die Link-Pair Kalkulation, welche wir auch in unserer Methodik vorstellen werden. Verwandte Arbeiten, welche wir für kleinere Aussagen als Referenz verwenden werden, allerdings auch wichtige Aspekte beinhalten sind: „Multilayer and Multiplex Networks: An Introduction to Their Use in Veterinary Epidemiology” von Kinsley AC, Rossi G, Silk MJ und VanderWaal K, „Foundations of Multidimensional Network Analysis” von Michele Berlingerio, Michele Coscia, Fosca Giannotti, Anna Monreale und Dino Pedreschi.
3. Methodik
3.1 Notation
Sei \(W\) ein Multilayer-Netzwerk, welches aus der Menge \(V\) besteht, die \(N\) Knoten enthält und \(l\) Kanten. \(l\) gibt dabei die Ebene an, die betrachtet wird. So existiert ein Multilayer-Netzwerk \(W\) mit \(W = (V, E(1), E(2), ..., E(L))\). Angenommen \(V\) bestehe hierbei aus \(V = {v_1, v_2, ...v_N }\), wobei dies die Menge aller Knoten darstellt. Des Weiteren sei \(C\) eine Ansammlung, welche Communities darstellt, so existiert \(C = {C_1, C_2, ..., C_q}\), dabei gilt \(C_i \subseteq V\).
Das Muster des Auftretens der Gemeinschaften ist nicht im Vorhinein bekannt, somit ist die Zusammenführung mehrerer Beobachtungen derselben Gemeinschaft nicht ohne Weiteres möglich. Aus diesem Grund gehen wir analog, wie im Paper von Yuming Huang et al. davon aus, dass es eine Zahl \(q\) gibt, welche Auskunft über die Anzahl der Communities vermittelt.
3.2 Modelle und Algorithmen
Es gab in der Vergangenheit diverse Versuche mit verschiedenen Ansätzen Communities in Multilayer-Netzwerke zu entdecken. Multilayer-Netzwerke zu analysieren bieten einen großen Mehrwert, da bei Single-Layer-Netzwerken oft viele Datensätze zur Analyse unzureichend sind. Deshalb befassen wir uns im Folgenden mit verschiedenen Methoden und Ansätzen zur Analyse von Multilayer-Netzwerken, wobei allerdings die meisten Ansätze für Monolayer-Netzwerke konzepiert wurden. Die Herausforderung von Overlapping Community Detection algorithms (OCDA) in Multilayer-Netzwerken ist es das Netzwerk in eine Menge von disjunktiv zusammenhängender Module zu unterteilen (Huang et al., 2020).
Erste Ansätze von Algorithmen auf Multilayer-Netzwerke beruhen darauf entweder Multilayer-Netzwerke in ein einziges Single-Layer-Netzwerk zu überführen oder die bestehenden Algorithmen für jede einzelne Ebene auszuführen und dann die Partitionen dieser am Ende zusammenzufügen. Jedoch wurden diese Ansätze kritisiert, da hierbei die Verbindungen zwischen den Ebenen vernachlässigt werden und die Ergebnisse nicht präzise sind. Algorithmen für Mulitlayer-Netzwerke werden in 3 Kategorien unterteilt:
- „flattening methods“
- „aggregation methods“
- „direct methods“
(Huang et al., 2020)
„flattening methods“ sind Methoden, in welchen die Daten von allen Ebenen in eine einzige Ebene überführt werden, um darauf die bestehenden Algortihmen, die für Monolayer-Netzwerke konzepiert wurden, anzuwenden. Da es bei dieser Methode nicht um die Algorithmen geht, sondern darum das Netzwerk an die bestehenden Algorithmen anzupassen, werden wir uns im Folgendem nicht genauer damit befassen.
„aggregation methods“ sind Methoden, die Communities in jeder Ebene entdecken und dann zusammenführen. Hierbei werden die Communities, die in jeder Ebene entdeckt werden um redundante Information reduziert. Allerdings ist die Laufzeit erhöht und die Methode braucht \(2^L\) Vergleiche. Es gibt einen einen Parameter \(P_{C_{k}}^{l}\), die für jede Ebene die Wahrscheinlichkeit von Communities beschreibt, um dann die Communities jeder Ebene in Form eines Korrelationskoeffizienten \(ραβ\) zwischen den Schichten \(α\) und \(β\) zusammenzuführen. Jedoch empfehlen sich diese Art von Methoden nicht, da einige Experimente auf Multilayer-Netzwerke zeigen, dass die Analysen in aggregierten Netzwerken inakkurat sind.
“direct methods” sind darauf abgezielt Community Strukturen direkt in Multilayer-Netzwerken zu finden. Es gibt viele solcher Algortihmen, die im letzten Jahrzehnt entwickelt wurden.
Im Folgenden befassen wir uns mit überlappenden Community Detection Algortihmen, die in Multilayer-Netzwerke adaptiert worden sind. D.h. bestehende Algorithmen, die bereits für Monolayer-Netzwerke existieren, werden so modifiziert, dass man diese auf Multilayer-Netzwerke anwenden kann.
3.3 improved lable propagation algorithm
„label propagation algorithm“ (kurz LPA) nutzt das Vermehren von Netzwerken aus. Raghavan et al. hat den LPA vorgeschlagen, um Communities in sozialen Netzwerken zu entdecken. Dieser Algorithmus benutzt nur die Netzwerkstruktur zu diesem Zweck. Es hat eine lineare Laufzeit und erzielt angemessene Ergebnisse. Diese Methoden erlauben es den Knoten Eigenschaften von deren Nachbarn zu übernehmen (Raghavan et al., 2007).
Der Prozess LPA läuft wie folgt ab:
Schritt 1: Durchquere das Netzwerk und initialiere jeden Knoten.
Schritt 2: Lege eine zufällige Reihenfolge der Knotenreihenfolge fest.
Schritt 3: Die Knoten werden in der Reihenfolge bearbeitet und kriegen die Eigenschaft, die die Mehrheit der benachbarten Knoten besitzt.
Schritt 4: Der Prozess wird iterativ durchgeführt, bis sich keine Eigenschaften von den Knoten mehr ändern.
Formal gilt für jeden Knoten \(v ∈ V\) aktualisiert v sein Label gemäß
\(l_{v}=\underset{l}{\arg \max } \sum_{u \in N(v)}\left[l_{u}==l\right]\)
(Cordasco & Gargano, 2012)
wobei \(l_V\) die Eigenschaft bzw. das „label“ von v erhält und
\(\left[l_{u}=l\right]= \begin{cases}1 & \text { if } l_{u}=l \\ 0 & \text { otherwise }\end{cases}\)
(Cordasco & Gargano, 2012)
Inspiriert von dem traditionellen LPA, entwickelte Alimadadi et al. (2019) den MNLPA (multilayer network label propagation algorithm), wo er die Nachbarschaften in Multilayer Netzwerken neu definierte. Der Algorithmus ist in folgenden Schritten unterteilt:
Schritt 1: Jeder Knoten \(u\) wird initialisiert und kriegt eine eindeutige Kennzeichnung, dann wird jeder Nachbarknoten von \(u\) in allen Ebenen, die wir erhalten, mit \(N_u\) markiert.
Schritt 2: Berechne die Ähnlichkeit zwischen u und v (nach folgender Tabelle) in \(N_u\) und markiere \(v\), wenn das Ergebnis größer ist als σ.
Schritt 3:
Wiederhole die Schritte, bis das Stoppkriterium erfüllt ist:
-die Knoten sind zufällig angeordnet
-Jeder Knoten \(u\), wovon jeder ähnlich markiert ist und Nachbarn die Eigenschaften an u übergeben, wird u mit der am häufigsten aufstretenen Eigenschaft markiert.
Schritt 4: Teile die Communities, mit Knoten die dieselbe Eigenschasften besitzen auf.
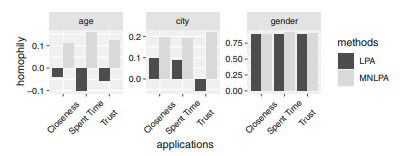
(Huang et al., 2021)
Vergleich zwischen LPA und MNLPA Algorithmen ausgehend von Facebook Datensätzen.
(Huang et al., 2021)
Vergleich zwischen LPA und MNLPA Algorithmen ausgehend von Facebook Datensätzen.

(Huang et al., 2021)
Die MNLPA ist effizient und in der Lage, mit gewichteten und direkten Netzwerken umzugehen, wird jedoch aufgrund der hohen Instabiliät kritisiert. Der MNLPA ist von diversen Experimenten mit echten Datensätzen verifiziert worden, dessen Ergebnisse in Bild 1 zu sehen sind.
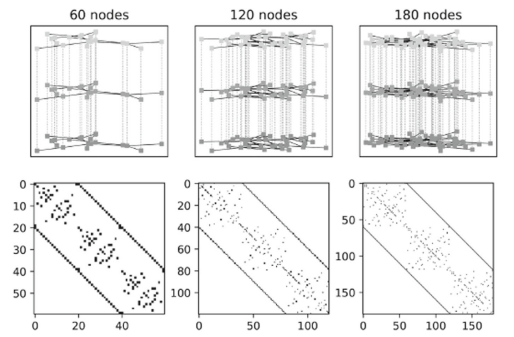
Da Facebook-Datensätze nicht bereitgestellt werden, konstruieren wir mehrere synthetische dreischichtige Netzwerke, wie in der Bild 2 dargstellt. Experimente an den konstruierten Netzwerken legen nahe, dass der MNLPA anspruchsvoll bei den Parametern ist. In Bild 3 sieht man, dass die Leistung der vorgeschlagenen MNLPA nicht zufriedenstellend sind.
Mit zunehmender Schwelle in \([0.2, 0.4]\) nahm die Modularität zu. Daher wird vermutet, dass der Schwellenwert größer als 0,4 sein sollte. In diesen Experimenten wurden nur gewichtete und gerichtete Datensätze verwendet, was in den Versuchsergebnissen deutliche Unterschiede hervorheben kann. MNLPA sind also für große Netzwerke unter den bestimmten Bedingungen (gewichtet und gerichtet) gut geeignet, wobei es für allgemeine Multilayer-Netzwerke notwendig ist, Änderungen hervorzunehmen, um die Leistung zu verbessern (Cordasco & Gargano, 2012).
3.4 Nonnegative matrix factorization methods
“Nonnegative matrix factorization” (kurz: NMF) sucht die nichtnegative Matrixfaktorisierung nach \(A ∈ R\) und \(S ∈ R\), so dass \(X ≈ AS\). Diese approximative Faktorisierung dient dazu, Merkmalsvektoren zu finden, die zusammen die Datenpunkte in X näherungsweise repräsentieren.(Neural Nonnegative Matrix Factorization For Hierarchial Multilayer Topic Modeling) Als Methoden, um Communities in Netzwerken zu erkennen, kann eine solche nicht-negative Matrix eine Adjazenzmatrix sein, wobei die Zielfunktion dargestellt werden kann als
\(\min _{U \geq 0, V \geq 0} L\left(A, U V^{T}\right)=\left\|A-U V^{T}\right\|_{F}^{2},\)
(Huang et al., 2021)
wobei A eine \(n \times n\) Adjazenzmatrix ist und \(U\) und \(V\) \(n \times n\) Matrizen sind. Der Rang \(k\) entspricht der Anzahl von geteilten Communities. Dieses Verfahren ist bekannt um Communities in komplexen Netzwerken zu entdecken. Aktuell wird diese Methode zu Erkennung von Communities in Multilayer-Netzwerken verwendet. Das Problem ist konvex in U und V getrennt, aber nicht in beiden zusammen. Daher kann man nicht erwarten immer ein globales Minimum zu finden. Allerdings gibt es techniken lokale Minima zu entdecken. Es handelt sich hierbei um eine quantitative Funktion (d. h. die Modularitätsdichte des Multilayer-Netzwerks), die beweist, dass die Spurenoptimierung der Multilayer Modularitätsdichtig gleichwertig mit den Zielfunktionen der OCDAs ist. Die Modularitätsdichte \(Q_d\) für \({V_c}_c=1^k\) definiert als
\(Q_{D}\left(\left\{V_{c}\right\}_{c=1}^{k}\right)=\sum_{c=1}^{k} \frac{L\left(V_{c}, V_{c}\right)-L\left(V_{c}, \bar{V}_{c}\right)}{\left|V_{c}\right|}\)
(Huang et al., 2021)
wobei \(Q_d({V_c}_c=1^)\) die Modularitätsdichte der Community Partitionen, k die Anzahl der Partitionen und $V_c$ zeigt die Anzahl der Partitionen nach Entfernen von \(V_c\).\(L(V_i, V_j)\) berechnet die Anzahl der Kanten zwischen \(V_i\) und \(V_j\) aus, definiert als
\(L\left(V_{i}, V_{j}\right)=\sum_{p \in V_{i, q} \in V_{j}} w_{p q}\)
wobei \(p\) und \(q\) Knoten von den Partitionen \(V_i\) und \(V_j\) sind. \(W_{pq}\) ist das Gewicht der Kante \((p, q)\) und ergibt 1 bei ungewichteten Netzwerken. Die Zielfunktionwird zu einem Oprimierungsproblem umgewandelt, als
\(Q_{D}^{\mathcal{G}}\left(\left\{V_{c}\right\}_{c=1}^{k}\right)=\frac{1}{m} \sum_{l=1}^{m} \sum_{c=1}^{k} \frac{L^{l}\left(V_{c}, V_{c}\right)-L^{l}\left(V_{c}, \bar{V}_{c}\right)}{\left|V_{c}\right|}\)
(Huang et al., 2021)
wobei \(L^l(V_i, V_j)\) der Gleichung für die \(l\) Ebene darstellt. \(Q_D^G({V_C}_c=1^k)\) ist die Zielfunkktion der Partitionen vom Multilayer-Netzwerk G. Die optimale Partitionierung \({V_c}_c=1^k\) für Multilayer-Netzwerke kann durch Maximierung der Modularitätsdichte in jeder Ebene wie folgt dargestellt werden
\(\left\{\begin{array}{l}
\max \left(Q_{D}^{1}\left(\left\{V_{c}\right\}_{c=1}^{k}\right)\right) <br>
\max \left(Q_{D}^{2}\left(\left\{V_{c}\right\}_{c=1}^{k}\right)\right) <br>
\cdots <br>
\max \left(Q_{D}^{m}\left(\left\{V_{c}\right\}_{c=1}^{k}\right)\right)
\end{array}\right.\)
(Huang et al., 2021)
Danach werden Teilgraphen mit Hilfe des Greedy-Algorithmus in Multilayer-Netzwerken entdeckt. Anschließend wir der NMF-Algorithmus in jeder Ebene angewendet. Um die Methoden zu verifizieren, werden Experimente mit verschiedenen Datensätzen durchgeführt. Die Komplexität diese Methode ist \(O(mn2k)\), wobei \(m\) die Anzahl der Ebenen und \(k\) die Anzahl der Partitionen ist. Daher ist dieser Algorithmus für besonders große Netzwerke nicht geeignet. Jedoch braucht der Algorithmus außerdem Informationen über die Anzahl der Zielgesellschaft und der Zersetzungsprozess könnte zeitaufwending sein (Huang et al., 2021).
3.5 Stochastisches Block Modell (SBM)
Das stochastische Blockmodell (SBM) ist ein Zufallsgraphenmodell mit Clustern. Es wird weithin als kanonisches Modell zur Untersuchung von Clustering und der Community Detection eingesetzt und bietet allgemein eine Grundlage für die Untersuchung der statistischen und rechnerischen Kompromisse, die
sich aus den Netzwerk- und Datenwissenschaften ergeben. (Abbe, 2018)
Das stochastische Blockmodell ist ein generatives Modell für Zufallsgraphen, das in der Regel
Netzwerke erzeugt, die eine Gemeinschaftsstruktur enthalten.
Das bedeutet, dass jeder Knoten eine feste Community-Bindung besitzt, die bestimmt, mit welcher Wahrscheinlichkeit eine Kante
zu anderen Knoten besteht. (Lee & J., 2019)
Um ein einfaches Beispiel von einem Stochastischem Block Model einzuführen gehen wir analog wie im Paper von Clement Lee und Darren J. Wilkinson vor und stellen zur Verständnis dieses abstrakte Themas eine Abbildung vor:
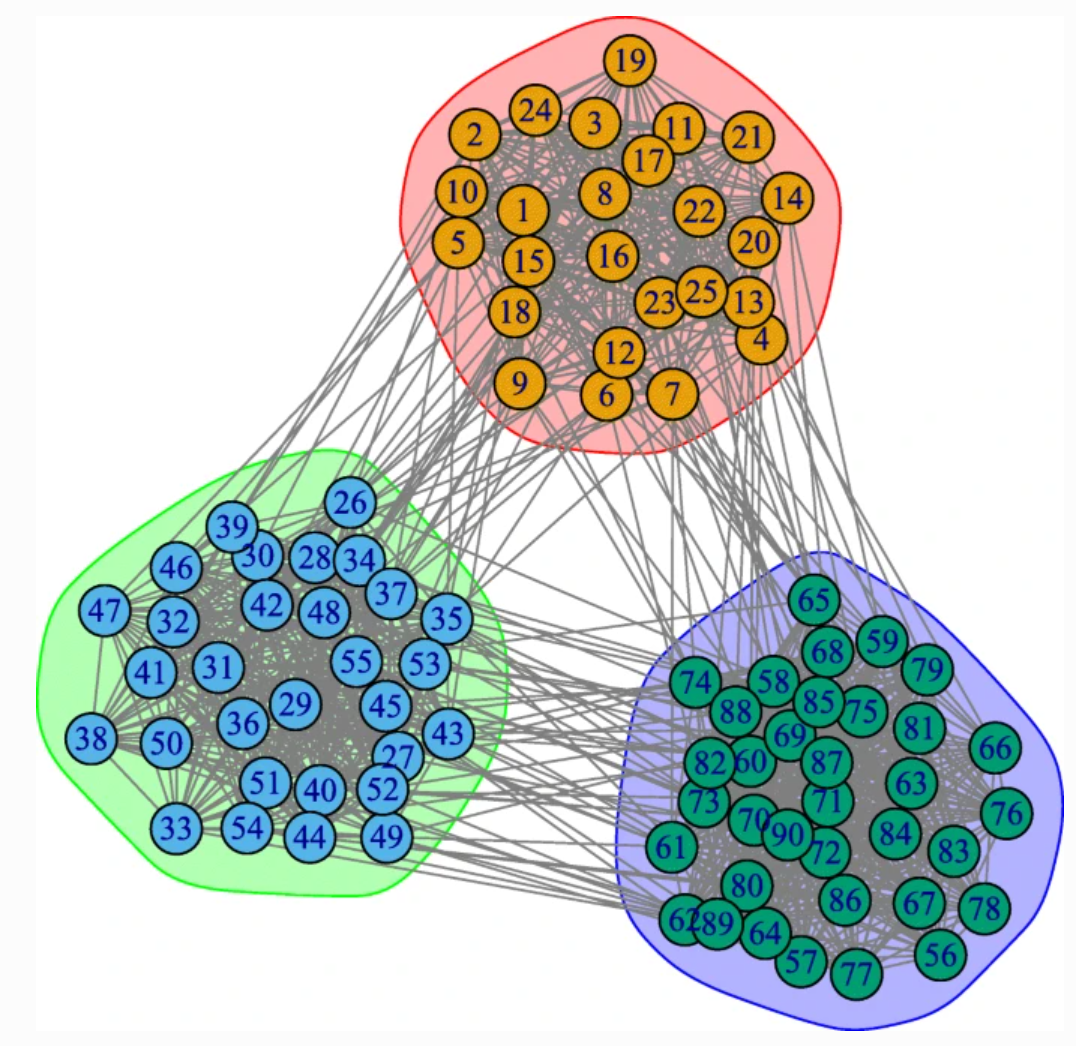
*Abbildung 1 (Lee & J., 2019)
Das vorgestellte Netz besteht aus 90 Knoten und 1192 Kanten. Die Knoten sind in drei Gruppen unterteilt. Die Gruppen 1, 2 und 3 erhalten jeweils 25, 30 und 35 Knoten. Die Knoten innerhalb der gleichen Gruppe sind enger miteinander verbunden als mit den Knoten einer anderen Gruppe. Außerdem ist das Konnektivitätsmuster eher “einheitlich”. Im Vergleich zu den Knoten 2 bis 25 scheint beispielsweise Knoten 1 nicht viel mehr mit anderen Knoten verbunden zu sein, weder innerhalb derselben Gruppe noch mit einer anderen Gruppe. Dieses Modell wird erzeugt, indem jedes Knotenpaar einzeln betrachtet und eine ungerichtete Kante zwischen ihnen simuliert wird. Die Wahrscheinlichkeit, eine solche Kante zu haben oder nicht, ist unabhängig von der Wahrscheinlichkeit eines anderen Knotenpaares. Für zwei Knoten in der gleichen Gruppe, d. h. mit der gleichen Farbe, beträgt die Wahrscheinlichkeit einer Kante 0,8, während für zwei Knoten in verschiedenen Gruppen die Wahrscheinlichkeit einer Kante 0,05 beträgt.
Yuming Huang et al. präsentieren in ihren Paper ebenfalls ein stochastisches Modell für ein Multilayer-Netzwerk, welches in diesem Paper auch vorgestellt und darauffolgend die Anwendung dieses auf ein Multilayer-Netzwerk dargestellt wird.
Das Modell beinhaltet eine Plausibilitätsfunktion \(P(W | C)\), und die damit zusammenhängenden Communities \(P(C)\).
Im Modell wird die maximale aposteriorische (MAP) Schätzung der Gemeinschaften dargestellt, die nach der Bayes-Regel berechnet wird:
(Huang et al., 2020)
Hierbei ist \(P(W) = \sum_{C'} P(W | C')P(C')\) eine Skalierungskonstante und kann aus der Optimierung ausgeschlossen werden. Es wird eine Darstellung der Gemeinschaften durch sogenanntes community labeling verwendet.
\(T = {t_i(l)}\), wobei \(i\) die Knoten der verschiedenen Ebenen von \(l\) veranschaulicht.
Durch das Bestehen einer Korrespondenz zwischen möglichen Gemeinschaften
\(C\) und des labeling \(T\), kann das Modell \(P(W|C)\) und \(P(C)\) dementsprechend äquivalent als \(P(W|T)\) bzw. \(P(T)\) ausgedrückt werden.
Auf ähnliche Weise können wir die MAP-Schätzung \(TˆMAP\) von \(T\) erhalten und die entsprechende Menge von Gemeinschaften finden, die mit \(CˆML\) übereinstimmt, aber wir greifen aus Gründen der numerischen Machbarkeit auf einen bekannten alternativen Ansatz zurück.
Bei diesem Ansatz berechnen wir zunächst die Randwahrscheinlichkeitsverteilung \(p_i,l( \alpha ) = P(t_i(l) = \alpha | W)\) der Etiketten \(\alpha\) eines einzelnen Knotens \(i\) in einer einzelnen Schicht \(l\). Dies lässt sich auch darstellen durch:
(Huang et al., 2020)
wobei die Verteilung \(P(T | W)\) nach der Bayes-Regel berechnet wird als:
(Huang et al., 2020)
Als Nächstes erhalten wir die maximale marginale Wahrscheinlichkeit (MMAP) der lable Schätzungen \(TˆMMAP = {tˆi,MMAP(l)}\) durch die individuelle Maximierung der resultierenden Randverteilungen Verteilungen \(p_i,l( \alpha )\) für jeden Knoten:
(Huang et al., 2020)
aus denen die entsprechenden Community Schätzungen \(CˆMMAP\) leicht erhalten werden können.
Im Folgenden verallgemeinern wir allerdings unserem Thema zugehörig SBM zur Beschreibung von überlappenden Gemeinschaftsstrukturen auf Multilayer-Netzwerke.
Die Idee hinter dem generativen Modell für Multilayer-Netzwerke ist, dass die gleiche Community in mehreren Schichten auftreten kann, somit wird nun ein Modell für overlapping SBM vorgestellt (OSBM).
Notation zur OSBM:
Sei \(n, t \in \mathbb{Z}_{+}, f:\{0,1\}^{t} \times\{0,1\}^{t} \rightarrow[0,1]\) und \(p, a\) eine Wahrscheinlichkeitsverteilung auf \(\{0,1\}^{t}\) .
Ein zufälliger Graph \(n, p, f\) wird auf der Scheitelpunktsmenge \([n]\) durch das unabhänigige Zeichnen von \(v \in[n]\) auf die Vektor-lable \(X(v)\) unter \(p\) generiert und indem man jede Kante unabhängig für jedes \(u, v \in[n], u < v\) zwischen u und v mit der Wahrscheinlichkeit f(X(u), X(v)) zeichnet. (Huang et al., 2020)
Wir gehen wie im Paper von Emmanuel Abbe auf ein Beispiel ein:
Man betrachte \(f(x, y)=\theta_{g}(x, y)\), während \(x_i\) etwas darüber aussagt, ob ein Knoten in die Gemeinschaft \(i\) gehört oder nicht. Des Weiteren sei gegeben
In dieser Gleichung zählt \(\langle x, y\rangle=\sum_{i=1}^{t} x_{i} y_{i}\) die Anzahl der gemeinsamen Gemeinschaften zwischen den Labels \(x\)
und \(y\), und \(g\). Zudem ist \(:\{0,1, \ldots, t\} \rightarrow[0,1]\) eine Funktion, die den Überschneidungswert in Wahrscheinlichkeiten umsetzt.
Wir können das OSBM als ein SBM mit \(k = 2^t\) Gemeinschaften darstellen, wobei jede Gemeinschaft ein mögliches Profil in \(\{0,1\}^{t}\) darstellt.
Ein vorgeführtes Beispiel ist dass, zwei sich überschneidende Gemeinschaften modelliert werden können, indem Knoten mit einem einzigen Attribut \((1, 0)\) und \((0, 1)\) jeder der disjunkten Gemeinschaften und Knoten mit beiden Attributen \((1, 1)\) der überlappenden Gemeinschaft zugewiesen werden, während Knoten
mit keinem der Attribute, d. h. \((0, 0)\), der Null-Gemeinschaft zugeordnet werden können.
Es wird nun angenommen, dass die Gemeinschaft \(i \in[k]\) mit dem Profil identifiziert wird, das der binären Erweiterung von \(i-1\) entspricht. Der Prior und die Konnektivitätsmatrix des entsprechenden SBM sind dann gegeben durch
W_{i, j} &=f(b(i), b(j)), \end{aligned}$$
wobei \(b(i)\) die binäre Erweiterung von \(i - 1\), und
ist. (Abbe, 2018)
3.5 Die Link Pair Kalkulation
Link Pair Definition:
Im Allgemeinen sind “Knotenpaare” und “Kantenpaare” in mehrschichtigen Netzen auch komplizierter. Bei Knotenpaaren ist es zum Beispiel offensichtlich, dass es in mehrschichtigen Netzen typischerweise mehr als eine Art von Kanten für ein Knotenpaar gibt, was bedeutet, dass die Existenz einer Kante keine binäre Frage mehr ist, sondern zu einer mehrwertigen Frage geworden ist. Gleichzeitig vermuten wir, dass die Knoten eines Knotenpaares aufgrund der Mehrschichteigenschaften auch dann miteinander kommunizieren können, wenn es in jeder Schicht keine direkte Kante innerhalb dieses Knotenpaares gibt. Nehmen wir die unten dargestellte Abbildung als Beispiel. Obwohl es keine direkte Verbindung von Knoten A zu Knoten D innerhalb einer der Schichten gibt, existiert ein Informationsflusspfad (rot markiert) von Knoten A zu Knoten D über das dreischichtige Netzwerk, was bedeutet, dass die Knoten A und D einen Weg haben, über die Schichten hinweg zu kommunizieren.
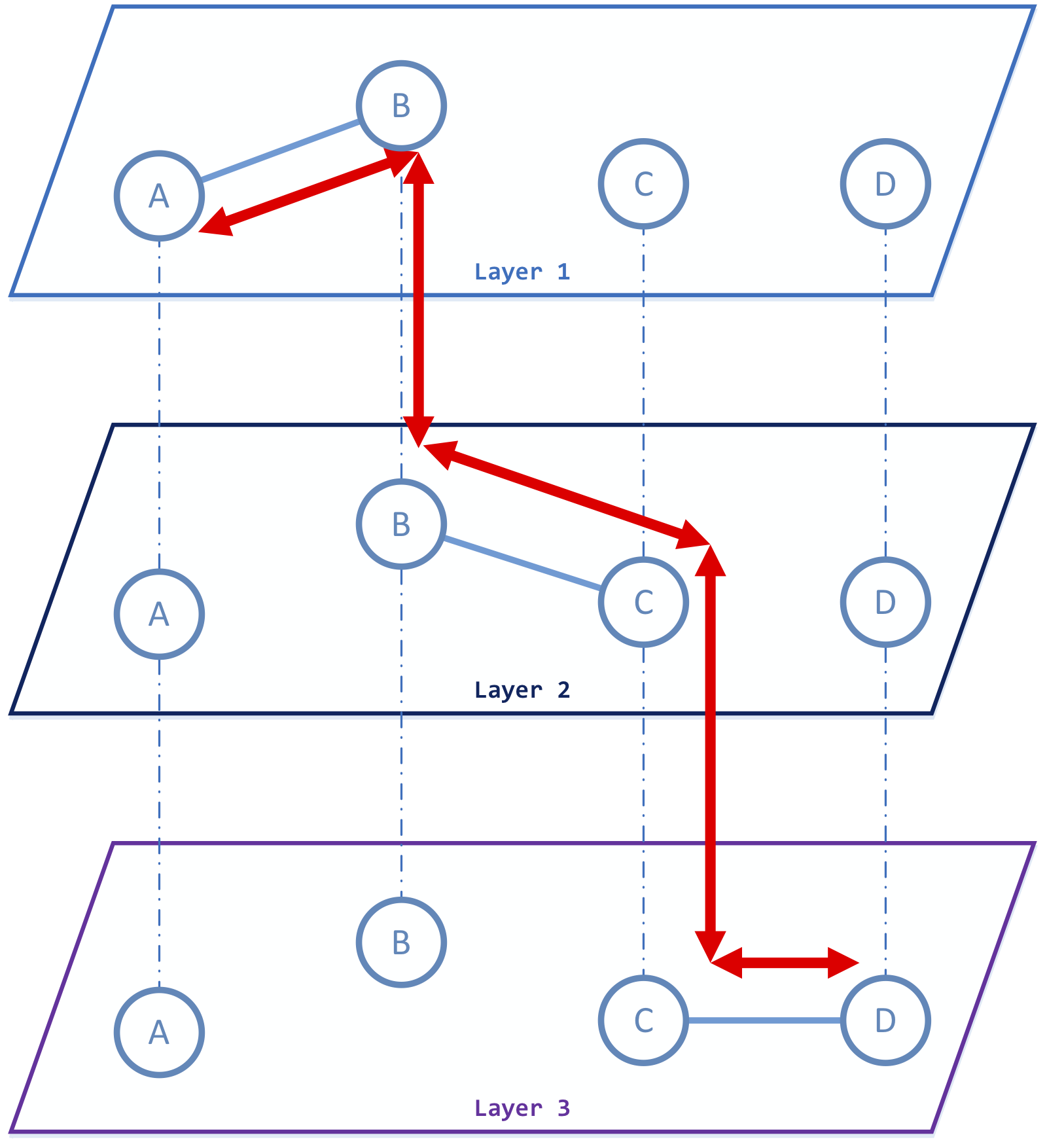
*Abbildung 1 (Liu et al., 2018)
Ein Beispiel für ein Knotenpaar, das in mehrschichtigen Netzen erreichbar ist: Die Information kann mit dem Knoten A beginnen und schließlich den Knoten D erreichen. Wenn man den gleichen Namen des Knotens B in Schicht 2 verwendet, kann die Information den Knoten C in Schicht 2 erreichen. Und dann, unter Verwendung des gleichen Knotens C in Schicht 3, erreicht diese Information schließlich den Knoten D in Schicht 3.
Der Hauptgrund für diesen Fall ist, dass wir in mehrschichtigen Netzen Kantenpaare nicht nur aus den “gleichen Schichten”, sondern auch aus den “anderen Schichten” bilden können.
Hier definieren wir “Link-Paare” anstelle von “Kantenpaaren”, um das Verbindungsverhalten für zwei Kanten in mehrschichtigen Netzen darzustellen:
Ein Link-Pair ist definiert als eine Kombination von “same-layer edge pairs” und “cross-layer edge pairs” aus mehrschichtigen Netzen. Wir sind der Meinung, dass die Verwendung von Verbindungspaaren in mehrschichtigen Netzen es uns ermöglicht, die einzigartige Struktur in jeder Schicht zu erhalten und gleichzeitig das Zusammenspiel zwischen den Schichten zu berücksichtigen. Wie in der Abbildung gezeigt, können wir durch die Verwendung von Link-Pairs in Netzwerken zwei Fälle von Wechselwirkungen zwischen Knoten A und Knoten D auf der Grundlage von drei Schichten erkennen. Ein solches Zusammenspiel gibt es jedoch in keiner der Schichten.
Eine weitere Methode zur overlapping Community Detection in Mulitlayer-Netzwerken ist die Link-Pair Kalkulation.
Die Berechnung der Ähnlichkeiten von Verbindungspaaren erfolgt in drei Schritten:
- Die Zusammenführen aller Schichten zu einem einheitlichen Netz,
- Das Extrahieren aller Verbindungspaare und
- Das Berechnen der Ähnlichkeiten für die Verbindungspaare.
Für den Zusammenführungsteil verwenden wir folgende Gleichung, um zu bestimmen, ob es eine Kante zwischen zwei Knoten gibt:
\(a_{i j}=\left\{\begin{array}{l} 1, \forall l \in L, \exists a_{i j}^{l}=1 \\ 0, \text { else } \end{array}\right.\)
(Liu et al., 2018)
Hier steht \({aij}\) für die Adjazenzmatrix für das vereinheitlichte Netzwerk und für die Adjazenzmatrix der Schicht \(l\). Diese Gleichung bestimmt, ob es eine Kante in einer Schicht gibt, und wenn es eine gibt, sollten wir die Kante zum vereinheitlichten Graphen hinzufügen. Der Vorteil hierbei ist, dass wir alle Verbindungspaare in mehrschichtigen Netzen leicht extrahieren können, da diese Verbindungspaare bereits durch die Gleichung in Kantenpaare in diesem vereinheitlichten Graphen umgewandelt worden sind.
Da die Ähnlichkeit von Kantenpaaren der gleichen Schicht und von schichtübergreifenden Kantenpaaren wahrscheinlich unterschiedlich ist, berechnen wir ihre Ähnlichkeiten getrennt. Nehmen wir die Abbildung als Beispiel. Dieses Beispiel zeigt schichtgleiche und schichtübergreifende Situationen für ein Verbindungspaar \(\left\{L_{\text {src } \leftrightarrow \text { mid }}, L_{\text {mid }} \leftrightarrow d s t\right\}\), das aus drei Knoten \(\{s r c, \text { mid }, d s t\}\) besteht. Für jeden Teilgraphen verwenden wir rote Knoten, um die gemeinsamen Nachbarn der Knoten \(src\) und \(dst\) darzustellen, deren Strukturinformationen bei der Ähnlichkeitsberechnung genutzt werden müssen, während die weißen und grünen Knoten die anderen Nachbarn von \(src\) und \(dst\) darstellen.
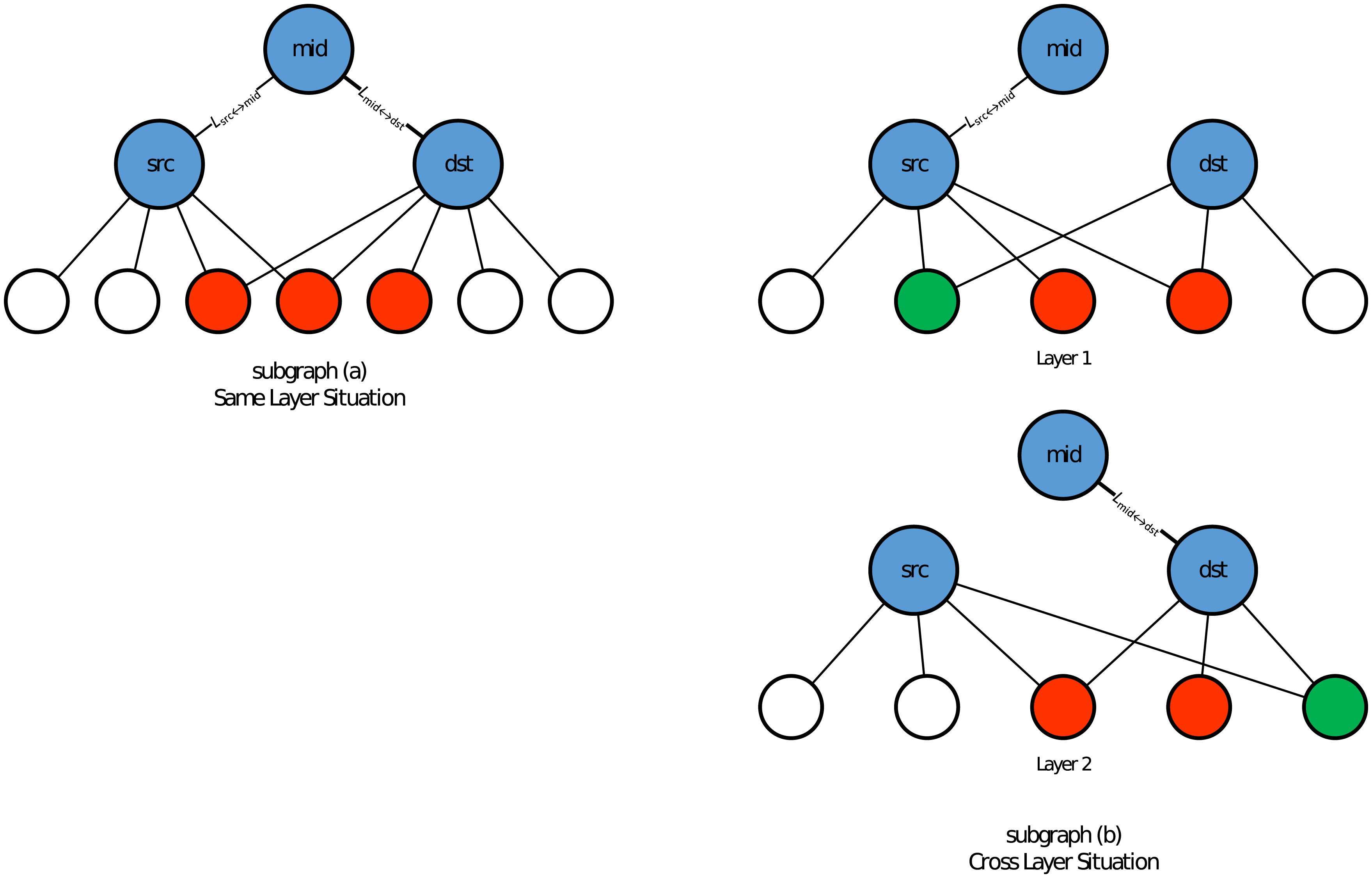
*Abbildung 2 (Liu et al., 2018)
Es liegt auf der Hand, dass in der ersten Teilgrafik alle drei gemeinsamen Nachbarn von \(src\) und \(dst\) für die Ähnlichkeitsberechnung verwendet werden sollten. In der zweiten Teilgrafik hingegen repräsentieren die grünen Knoten die gemeinsamen Nachbarn nur in einer Ebene, während die roten Knoten die gemeinsamen Nachbarn in beiden Ebenen darstellen. Hier berechnen wir nur die Ähnlichkeiten für die roten Knoten.
Hier wird die Jaccardsimilarität verwendet (auf welche verständnishalber nicht näher eingegangen wird), um die Ähnlichkeit des Linkpaares \(\left\{L_{s r c} \leftrightarrow \operatorname{mid}, L_{\text {mid }} \leftrightarrow d s t\right\}\) zu berechnen, siehe folgende Gleichung:
Zusätzlich wird ein Moderatorparameter eingeführt \(\alpha \in[0,1]\), um die schichtübergreifende Ähnlichkeit \(\text { crosslayerSim }\left(L_{s r c \leftrightarrow m i d}, L_{m i d \leftrightarrow d s t}\right)\) zu gewichten. (Liu et al., 2018)
IV. Resultate
Abwägend kann man sagen, dass es bereits viele OCDA gibt, welche sich auf Multilayer-Netzwerke adaptieren lassen. Mit der Zeit entwickeln sich Algorithmen und Modelle, sodass eine solche Adaption nicht nur ausschließlich auf Single-Layer Netzwerken funktioniert. Algorithmen die wir zum Zweck dies zu zeigen nutzten, sind der „label propagation algorithm“, die „non-negative matrix factorisation“, das Stochastische Block Modell und die Link-Pair Kalkulation. Anhand dieser Algorithmen und dem Model, sowie der Kalkulation lassen sich bereits OCDA in Multilayer-Netzwerke adaptieren, es sollte jedoch nicht ausser Acht gelassen werden, dass es noch zahlreiche weitere solcher Algorithmen und Modelle gibt, welche alle auf verschiedene Art und Weise für dieselbe Adaption sorgen.
Die Algorithmen bieten einen großen Mehrwert, da diese klassisch und schon bekannte Algorithmen sind. Unter den adaptierten Algorithmen gibt es nicht effiziente Algorithmen, die dafür stabil sind, genauso wie instabile Algorithmen, welche andererseits relativ effizient sind. Beispielsweise das „improved label propagation algorithm“ ist nicht deterministisch und instabil, dafür jedoch relativ effizient.
Die NMF Methoden hingegen sind stabil, aber ineffizient. Allerdings haben die Algorithmen insgesamt eine hohe Berechenbarkeitskomplexität. Für die Zukunft ist also noch viel zu tun, wie die Entwicklung effizienterer Algorithmen für Netzwerke mit vielen Ebenen zu ermöglichen. Außerdem könnten sich neuartige Algorithmen, je nach Zweck, besser eignen, weshalb es sich lohnt diese ebenfalls anzuschauen.
Zum Stochastischen Blockmodell lässt sich viel positives sagen. Blockmodelle haben ihren Ursprung in der Erforschung sozialer Netze:
Die Idee war, die Knoten des Netzes in verschiedene Gruppen oder “Blöcke” aufzuteilen, wobei alle Knoten im selben Block das gleiche Verbindungsmuster zu Knoten in anderen Blöcken aufweisen. Ursprünglich war dies zwar ein recht starres Konzept, das sich für eine abstrakte Algebra eignete, jedoch schwächt das SBM diese Vorstellung ab: Die Wahrscheinlichkeit einer Kante zwischen zwei Knoten hängt nur davon ab, in welchen Blöcken sie sich befinden, und ist unabhängig von den Kanten. Sie haben sich als nützliches statistisches Modell für die Entdeckung von Gemeinschaften erwiesen, dies ließ sich auch in diesem Paper vor allem durch SBM zur Beschreibung von überlappenden Gemeinschaftsstrukturen auf Multilayer-Netzwerke mithilfe von OSBMs erweisen.
Schlussendlich ist auch die Link-Pair Kalkulation ein toller Ansatz überlappende OCDA auf Multilayer-Netzwerke zu adaptieren. Im Gegensatz zu anderen Methoden zur Entdeckung von überlappenden Gemeinschaften in mehrschichtigen Netzwerken behandelt diese Methode Kantenpaare innerhalb von Schichten und zwischen Schichten als die grundlegenden Elemente zur Bildung von Gemeinschaften. Im Allgemeinen konzentrieren wir uns hauptsächlich darauf, wie das Zusammenspiel zwischen den Schichten erfasst werden kann. Es werden sowohl “same-layer”- als auch “cross-layer”-Kantenpaare als einen Weg für den Informationsfluss betrachtet, und es wird eine Methode zur Berechnung der Dichtheit der Community vorgeschlagen. Obwohl die Evaluierungsergebnisse aus Datensätzen zeigen, dass diese Methode die meisten Kanten in richtige Gemeinschaften aufteilen kann, gibt es einen Fall, in dem unsere Methode versagen kann: Wenn zwei Teile einer Gemeinschaft oberhalb des “Schnittkriteriums” verschmolzen sind, kann diese Methode diese beiden Teile als zwei separate Gemeinschaften behandeln.
V. Zusammenfassung
Alle die von uns genannten Algorithmen und Methoden bieten eine umfassende Community Detection auf Multilayer Netzwerke, und weisen -falls überhaupt- nur kleine Schwächen auf, welche verbessert werden können.
Im Verlauf der Arbeit wurde ein umfassender Überblick über die Blockmodellanalyse gegeben. Dabei zeigte sich, dass die Blockmodellanalyse sowohl bezüglich ihrer
theoretischen Vorbedingungen als auch bezüglich ihrer methodischen Anwendung ein komplexes Verfahren darstellt. Die Arbeit zeigt auch, dass verschiedene Modelle eine gute Herangehensweise an die “Community Detection” ist, so stellten wir zunächst das klassische Stochastische Block Modell vor und führten im Anschluss das OSBM für überlappende Gemeinschaften in Multilayer-Netzwerken vor, welche unserer Ansicht nach beiderlei reichliche Informationen zur Gemeinschaftserkennung in mehrschichtigen Netzwerken überreichen.
Des Weiteren haben wir die Link-Pair Kalkulation vorgestellt. Diese Methode ist in der Lage, die Informationen innerhalb jeder Schicht zu erhalten und das Zusammenspiel zwischen den Schichten zu nutzen. Indem wir sowohl schichtgleiche als auch schichtübergreifende Kantenpaare berücksichtigen, bildet diese Methode eine hierarchische Struktur der mehrschichtigen Netzwerke, wobei die grundlegenden Elemente hierbei die Kanten sind. Darüber hinaus haben wir einen realen Datensatz verwendet, um zu beweisen, dass alle schichtgleichen und schichtübergreifenden Kantenpaare berücksichtigt werden sollten.
Abschließend sind wir der Meinung, dass die Informatik viele Algorithmen bietet, um Communitys in Multidimensionalen Netzwerken ausfindig zu machen. Allerdings sind wir auch der Ansicht, dass die Wissenschaft bei der Neuerschaffung von solchen Algorithmen an seine Grenzen stößt und auf traditionelle OCDA zurückgegriffen werden sollte bzw., dass es vielleicht sogar zu Modifizierungen solcher Algorithmen kommen sollte, um effizienter in der Forschung Voranzuschreiten. Die Algortihmen sind also nicht perfekt und weisen dennoch schwächen auf.
Unter anderem verschlechtert sich die Leistung dieser Algorithmen erheblich, wenn die Anzahl der Gemeinschaften pro Knoten zunimmt. Außerdem sind die meisten Algorithmen, nicht in der Lage, jeden Knoten der richtigen Anzahl von Gemeinschaften zuzuordnen. Im Allgemeinen sind die
meisten der von uns untersuchten Algorithmen nur in der Lage, überlappende Gemeinschaften in Netzwerken mit einer geringen Anzahl von überlappenden Knoten und einer geringen Anzahl von Gemeinschaften pro Knoten zu erkennen.
Schließlich zeigen unsere Ergebnisse, dass die Mehrzahl der Algorithmen zur Erkennung überlappender Gemeinschaften mit einer hohen Anzahl von überlappenden Knoten oder einer hohen Anzahl von Gemeinschaften pro Knoten nicht gut funktionieren können. Daher könnten sich die zukünftigen Arbeiten in diesem Forschungsgebiet entweder auf die Entwicklung neuer Algorithmen zur Erkennung von überlappenden Gemeinschaften konzentrieren, oder auf den von uns genannten Hinweis eingehen und bereits bestehende Algorithmen so abändern, dass sie noch weniger Schwächen aufweisen und auch in Netzwerken mit einer hohen Anzahl überlappender Knoten gut funktionieren, gleichzeitig aber deren Leistung in Netzwerken mit einer hohen Anzahl von Gemeinschaften pro Knoten konstant stabil bleibt.
VIII. Referenzen
- Foundations of Multidimensional Network Analysis. (2011). Proceedings - 2011 International Conference on Advances in Social Networks Analysis, 485. https://doi.org/10.1109/ASONAM.2011.103
- Kinsley AC, S. M. J., Rossi G, & K, V. W. (2020). Multilayer and Multiplex Networks: An Introduction to Their Use in Veterinary Epidemiology. https://doi.org/10.3389/fvets.2020.00596
- Huang, Y., Panahi, A., Krim, H., & Dai, L. (2020). Community Detection and Improved Detectability in Multiplex Networks. IEEE Transactions on Network Science and Engineering, 7(3), 1697–1709. https://doi.org/10.1109/tnse.2019.2949036
- Raghavan, U. N., Albert, R., & Kumara, S. (2007). Near linear time algorithm to detect community structures in large-scale networks. Phys. Rev. E, 76(3), 036106. https://doi.org/10.1103/PhysRevE.76.036106
- Cordasco, G., & Gargano, L. (2012). Label propagation algorithm: A semi-synchronous approach. Int. J. of Social Network Mining, 1, 3–26. https://doi.org/10.1504/IJSNM.2012.045103
- Huang, X., Chen, D., Ren, T., & Wang, D. (2021). A survey of community detection methods in multilayer networks. Data Mining and Knowledge Discovery, 35(1), 1–45. https://doi.org/10.1007/s10618-020-00716-6
- Abbe, E. (2018). Community Detection and Stochastic Block Models: Recent Developments. Journal of Machine Learning Research, 18(177), 1–86. http://jmlr.org/papers/v18/16-480.html
- Lee, W., Clement, & J., D. (2019). A review of stochastic block models and extensions for graph clustering. Applied Network Science, 4(122). https://doi.org/10.1007/s41109-019-0232-2
- Liu, W., Suzumura, T., Ji, H., & Hu, G. (2018). Finding overlapping communities in multilayer networks. PLOS ONE, 13(4), e0188747. https://doi.org/10.1371/journal.pone.0188747