Neue OCDA für vorzeichenbehaftete Netzwerke
| Marco Heinisch | Maximilian Tenten | Michael Kewa | ||||
|---|---|---|---|---|---|---|
| RWTH Aachen University | RWTH Aachen University | RWTH Aachen University | ||||
| marco.heinisch@rwth-aachen.de | maximilian.tenten@rwth-aachen.de | michael.kewa@rwth-aachen.de |
Abstract
Aufgrund der zunehmenden Datenmenge von sozialen und politischen Netzwerken im Internet gewinnt die Analyse dieser Daten durch Overlapping Community Detection Algorithmen (OCDA) stetig an Bedeutung.
Da Beziehungen auf solchen sozialen Netzwerken als positiv (“Freund”, “Sympathie”) und negativ (“Feind”, “Abneigung”) klassifiziert werden können, lassen sich diese als vorzeichenbehaftete Netzwerke abstrahieren. Durch neue OCDAs für solche Netzwerke können beispielsweise überlappende gesellschaftliche Gruppierungen und politische Meinungsfelder besser identifiziert, analysiert und beschrieben werden.
Ziel dieser Arbeit ist es, einige für vorzeichenbehaftete Netzwerke neu entwickelte Community Detection Algorithmen in deutscher Sprache vorzustellen, deren Funktionsweise zu erläutern und sie in Hinblick auf Ergebnisse und Laufzeit zu vergleichen.
Keywords
Community Detection, vorzeichenbehaftete Netzwerke, Overlapping Communities
Inhaltsverzeichnis
Einleitung
Mithilfe von OCDAs werden Communities in Netzwerken identifiziert. Netzwerke lassen sich unter anderem in Unsigned Networks (non-SN) und signed Networks (SN) klassifizieren. Die Kanten in non-SN repräsentieren vorzeichenlose Verbindungen zwischen Knoten. Die Kanten in SN verfügen über die Eigenschaft vorzeichenbehaftet zu sein. Viele bekannte Community-Detection (CD) Algorithmen können ausschließlich vorzeichenlose Kanten verarbeiten (Liu et al., 2014). Diese Kategorie an CDs wird als vorzeichenlos bezeichnet. Jedoch spiegeln vorzeichenlose Netzwerke weitgehend nicht genau die sozialen Beziehungen der realen Welt dar. Komplexe und individuelle menschliche Beziehung werden in vorzeichenlosen Netzwerken nur als Kanten verkörpert und schöpfen somit das Potenzial der Netzwerke nicht komplett aus. Um die Informationsdichten in Netzwerken zu maximieren, bieten sich SNs sehr gut an. Mit der steigenden Nutzung und Relevanz von SNs sind Methoden nötig, welche SNs verarbeiten können. Im Zuge unserer Ausarbeitung werden zwei Algorithmen thematisiert, die SNs verarbeiten und innerhalb dieser Communities erkennen können.
Verwandte Arbeiten
Der erste, hier aufgeführte Algorithmus MEA\(_s\)-SN wurde von (Liu et al., 2014) 2014 in ihrem Paper vorgestellt. Einige Ansätze erweiterten die Autoren hierbei von (Liu et al., 2010) auf vorzeichenbehaftete Netzwerke.
Der zweite Algorithmus MACD-SN wurde 2020 VON (Che et al., 2020) publiziert. Unsere Arbeit basiert überwiegend auf diesen genannten Beiträgen.
Methodik
Im Folgenden möchten wir in der Begriffserklärung einige Begriffe erläutern, die als Hintergrundwissen für das Verständnis des Kapitels notwendig sind. Weiterhin stellen wir die Notation und eine der beiden üblichen Problemrepräsentationen innerhalb von Algorithmen zur Erkennung von Communities in vorzeichenbehafteten Netzwerken vor. Im Abschnitt Algorithmen werden die beiden Algorithmen MEA\(_s\)-SN und MACD-SN behandelt, wobei zuerst algorithmusspezifische Funktionen und Eigenschaften erläutert werden und anschließend der jeweilige Algorithmus selbst als Ganzes vorgestellt wird.
Begriffserklärung
Vorzeichenbehaftete Netzwerke
Wie bereits in den vorhergehenden Teilen erwähnt, versteht man unter vorzeichenbehafteten Netzwerken, Netzwerke deren Kanten entweder ein positives Vorzeichen (positive Verbindung, bspw. Freundschaft) oder ein negatives Vorzeichen (negative Verbindung, bspw. Feindschaft) haben. Um dies darzustellen, eignen sich beispielsweise Graphen mit positiven und negativen Kantengewichten, man kann allerdings auch mit einer Darstellung ohne Kantengewichte auskommen. Wir stellen im Abschnitt Notation Varianten beider Arten vor, da diese auch beide von den Autoren der von uns betrachteten Algorithmen verwendet werden.
Evolutionäre Algorithmen
Evolutionäre Algorithmen (EA) sind an der in der Natur auftretenden Revolution von Lebewesen orientierte Optimierungsverfahren. EAs werden hauptsächlich zur Suche eingesetzt. So werden analog zur Natur Gene betrachtet, die von Generation zu Generation Mutationen ausgesetzt sind, von denen sich manche auf die folgenden Generationen (durch Fortpflanzung) auswirken. Ein vereinfachter Ablauf kann sich so vorgestellt werden: Man wählt eine anfangs meist zufällige Menge von Lösungskandidaten, welche auch als Chromosome bezeichnet werden (siehe Problemrepräsentation). Diesen wird nun durch Evaluation durch eine sogenannte Fitnessfunktion ein Wert zugeordnet. Anschließend werden, sofern sie stattfindet, Chromosome für die Rekombination ausgewählt und kombiniert. Nach einer zufälligen Änderung (Mutation) der Nachfahren wird die nun entstandene Generation erneut evaluiert und die nächste Generation selektiert. Durch diese Vorgehensweise wird zwar nicht immer die beste Lösung, aber mindestens eine hinreichende Lösung gefunden.
Memetische Algorithmen
Memetische Algorithmen sind eine Unterklasse genetischer Algorithmen, die wiederum eine Unterklasse Evolutionärer Algorithmen bezeichnen. Diese Algorithmen zeichnen sich dadurch aus, dass sie um lokale Suchfunktionen erweitert wurden, um die Wahrscheinlichkeit einer vorzeitigen Konvergenz zu vermindern.
Notation
Grundsätzlich werden vorzeichenbehaftete Netzwerke als Graphen notiert, deren Kanten entweder ein positives oder negatives Vorzeichen besitzen. Es muss allerdings nicht zwingend eine Gewichtung vorliegen, wie wir auch an den beiden unterschiedlichen Notationen der Autoren unserer betrachteten Algorithmen beobachten können. (Liu et al., 2014) setzen tatsächlich auf eine Gewichtung ihrer Kanten:
Ein Netzwerk \(N\) ist ein ungerichteter Graph definiert als \(N=(V,E,w)\) wobei \(\{v_1,v_2,v_3,\dots,v_n\}\) die Knoten, \(E\subseteq V\times V=\{(v_i,v_j)\mid v_i,v_j\in V\land i\neq j\}\) die Kanten und \(w(v_i,v_j)\) das Gewicht der Kante zwischen \(v_i\) und \(v_j\) abgeben. Für \(w\) gilt entweder \(w>0\) wenn eine positive Beziehung vorliegt, oder \(w<0\) bei einer negativen Beziehung.
Anders dazu nutzen (Che et al., 2020) lediglich einen ungerichteten Graphen ohne Gewichtung und stellen stattdessen die positiven und negativen Beziehungen innerhalb der Adjazenzmatrix des Graphen dar:
Ein Netzwerk \(N\) ist ein ungerichteter Graph definiert als \(N=(V,E)\) wobei \(\{v_1,v_2,v_3,\dots,v_n\}\) die Knoten, \(E\subseteq V\times V=\{(v_i,v_j)\mid v_i,v_j\in V\land i\neq j\}\) die Kanten und \(A=(A_{ij})_{nxn}\) die Adjazenzmatrix abgeben, mit \(A_{ij}=1\) wenn eine positive Beziehung vorliegt, \(A_{ij}=-1\) wenn eine negative Beziehung vorliegt und \(A_{ij}=0\) wenn keine Beziehung vorliegt.
Um den Unterschied zwischen positiven und negativen Beziehungen in einem Graphen sichtbar zu machen, werden positive Beziehungen grundsätzlich mit durchgezogenen Kanten und negative Beziehungen mit gestrichelten Kanten dargestellt.
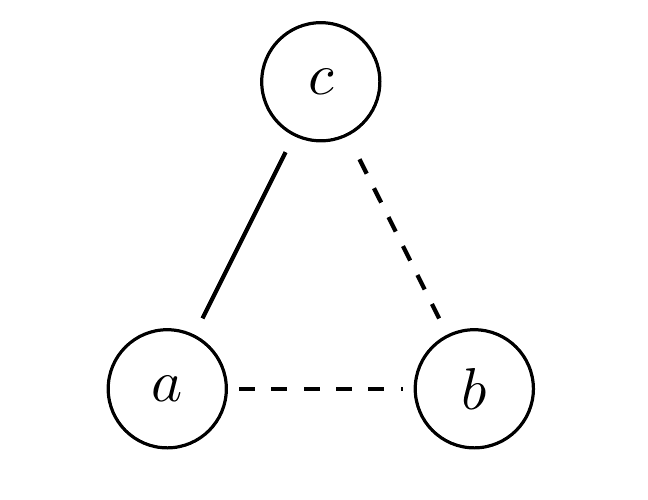 Abbildung 1: Beispiel positive und negative Beziehungen
Abbildung 1: Beispiel positive und negative Beziehungen
Somit sind sowohl \(N_w=(V,E,w)\) mit \(V=\{a,b,c\},E=\{(a,b),(a,c),(b,c)\}\) und \(w(a,b)=-1,w(a,c)=1,w(b,c)=-1\) als auch \(N_u=(V,E)\) mit den selben \(V,E\) und Adjazenzmatrix \(A=\left(\begin{array}{cc} 0 & -1 & 1 \\ -1 & 0 & -1 \\ 1 & -1 & 0 \end{array}\right)\) korrekte Notationen für den Beispielgraphen Abb. 1.
Natürlich können in der Notation von (Liu et al., 2014) Kantengewichte auch andere Zahlen als 1 oder -1 annehmen, sie bilden damit also eine präzisere Variante Beziehungen auszudrücken, da sie auch etwas über die Ausprägung der negativen oder positiven Beziehung aussagen. So steht ein Gewicht weiter weg von 0 für eine stärker positive oder negative Beziehung als ein Gewicht näher zur 0. Diese Unterscheidung ist wichtig für den MEA\(_s\)-SN Algorithmus, da mit Hilfe dieser Gewichte der Begriff von Ähnlichkeit definiert wird, welchen wir in dem Kapitel des Algorithmus weiter erläutern werden.
Problemrepräsentation
In evolutionären Algorithmen spricht man von direkter oder indirekter Repräsentation eines Problems. Bei direkter Problemrepräsentation handelt es sich um natürliche Repräsentationen, die direkt evaluiert werden können, in denen also Problem- und Suchraum identisch sind. Bei indirekter Repräsentation dagegen ist die Repräsentation der Lösung an sich nicht vollständig, um evaluiert zu werden, sondern muss zunächst von einem Dekodierer in eine direkte Repräsentation umgewandelt werden (Liu et al., 2014). Eine indirekte Repräsentation kann ggf. die Performance eines Algorithmus verbessern, steigert aber auch den Aufwand durch das Ausführen des Dekodierers bei jedem Aufruf.
Die beiden üblichen direkten Problemrepräsentationen bei evolutionären und memetischen Algorithmen zur Entdeckung von Communities sind string-basierte (Tasgin et al., 2007) und orts-basierte (Shi et al., 2012) Kodierung. Beide unsere betrachteten Algorithmen nutzen oder erweitern die string-basierte Kodierung von Netzwerken, weshalb wir diese hier kurz erklären möchten:
Jeder mögliche Kandidat für eine Aufteilung in Communities wird dargestellt durch ein sogenanntes Chromosom, eine Menge mit der gleichen Mächtigkeit wie die potentiellen Mitglieder unserer Communities. Bei einem Netzwerk mit \(n\) Nutzern hat jedes Chromosom also Mächtigkeit \(\mid ch_j \mid = n\). Als Population bezeichnen wir die Menge aller Chromosome, also \(popu=\{ch_1,ch_2,\dots,ch_q\}\) wobei \(ch_j\) das Chromosom an \(j\)-ter Stelle ist und \(q\) die Anzahl Chromosome innerhalb der Population. Jedes Chromosom besteht aus einer Menge von Genen \(ch_j=[ge_1,ge_2,\dots,ge_n]\) wobei jedes Gen einen Wert der Menge \(\{1,2,\dots,n\}\) annimmt. Das Gen \(ge_j\) an \(j\)-ter Stelle stellt hierbei gerade da zu welcher Community der Knoten/Nutzer \(v_j\) gehört (Che et al., 2020).
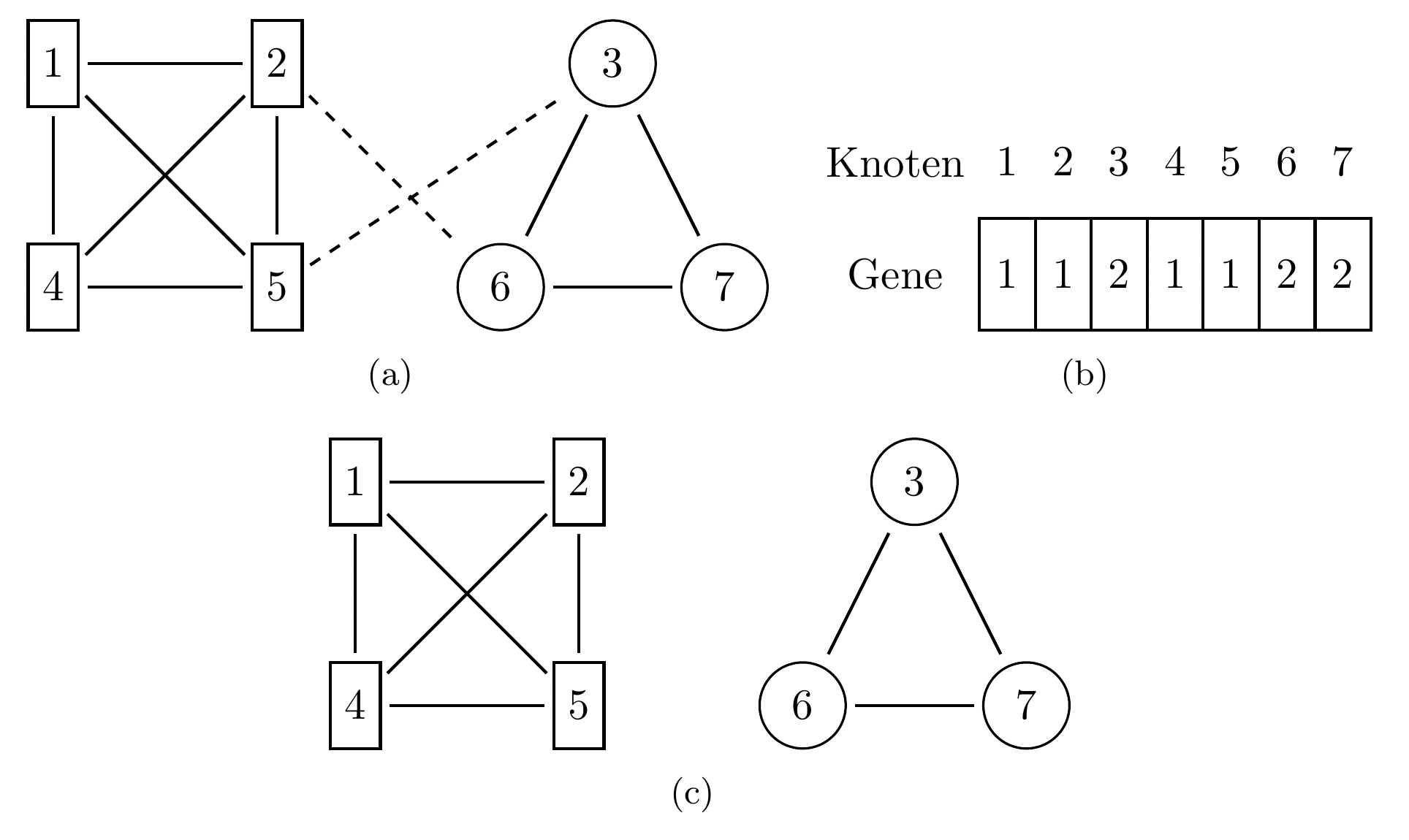 Abbildung 2: Beispiel Repräsentation (analog zu(Che et al., 2020))
Abbildung 2: Beispiel Repräsentation (analog zu(Che et al., 2020))
Wie man in Abb 2(b) sehen kann, wird in den Genen jeweils der Index der Community, denen ein Knoten zugehört gespeichert. So bilden Knoten 1, 2, 4, 5 eine Community in Abb 2(a) und dementsprechend sind \(ge_1=1,ge_2=1,ge_4=1,ge_5=1\). Und da die Knoten 3, 6, 7 eine weitere Community bilden, gilt für die übrigen Gene: \(ge_3=2,ge_6=2,ge_7=2\). Ein Nachteil dieser Repräsentation fällt schnell auf, da sich überschneidene Communities nicht innerhalb eines Chromosoms dargestellt werden können. Dieses Problem lösen (Liu et al., 2014) durch eine angepasste Darstellung in ihrem Algorithmus, auf die wir in der Methodik eingehen werden.
Algorithmen
Multiobjective Evolutionary Algorithm for Signed social Networks (MEA\(_s\)-SN)
MEA\(_s\)-SN ist ein ein evolutionärer Algorithmus, welcher auf vorzeichenbehafteten, ungerichteten Graphen arbeitet und in der Lage ist, sowohl überlappende als auch separierte Communities zu erkennen. In der nachfolgenden Beschreibung beschränken wir uns überwiegend auf die OCD-Funktionalität.
Strukturelle Ähnlichkeit
MEA\(_s\)-SN basiert stark auf der Verwendung der sogenannten strukturellen Ähnlichkeit. Der Begriff der strukturellen Ähnlichkeit wurde für gewichtete ungerichtete Netzwerke von (Huang et al., 2011) eingeführt um die lokale Konnektivitätsdichte zweier benachbarter Knoten zu beschreiben. Seien \(u,v\in V\) zwei Knoten aus einem gewichteten ungerichteten Netzwerk dann ist die Ähnlichkeit \(s(u,v)\) definiert durch (Huang et al., 2011):
\[s(u,v)=\frac{\sum\limits_{x\in\Gamma(u)\cap\Gamma(v)}w(u,x)\cdot w(v,x)}{\sqrt{\sum\limits_{x\in\Gamma(u)}w^2(u,x)}\cdot\sqrt{\sum\limits_{x\in\Gamma(v)}w^2(v,x)}}\]wobei \(\Gamma(y)\) mit \(y\in V\) für die Menge mit \(y\) selbst und seinen Nachbarknoten steht, also
\[\Gamma(y)=\{v\in V\mid(y,v)\in E\}\cup\{y\}.\]Strukturelle Ähnlichkeit ist allerdings nur für gewichtete Netzwerke ohne Vorzeichen definiert, weshalb (Liu et al., 2014) den Begriff auf vorzeichenbehaftete Netzwerke erweitern. Ihre Änderungen basieren auf der Theorie des sozialen Gleichgewichts ((Easley & Kleinberg, 2010), (Tang et al., 2012)), welche aussagt, dass Menschen in sozialen Netzwerken sich grundsätzlich in ausgeglichene Netzwerke eingliedern. Für eine Dreiecksbeziehung bedeutet dies beispielsweise, dass entweder alle drei Personen miteinander befreundet sind, oder nur eins der Paare befreundet ist (siehe Abb 1). Dadurch entstand die folgende Definition \(s_\text{signed}(u,v)\) für zwei Knoten \(u,v\in V\) in einem vorzeichenbehafteten, gewichteten, ungerichteten Netzwerk (Liu et al., 2014):
\[s_\text{signed}(u,v)=\frac{\sum\limits_{x\in\Gamma(u)\cap\Gamma(v)}\psi(x)}{\sqrt{\sum\limits_{x\in\Gamma(u)}w^2(u,x)}\cdot\sqrt{\sum\limits_{x\in\Gamma(v)}w^2(v,x)}}\]mit
\[\psi(x)=\left\{\begin{array}{cc} 0 & \text{falls }w(u,x)<0\text{ und }w(v,x)<0 \\ w(u,x)\cdot w(v,x) & \text{sonst.} \end{array}\right.\]Angepasste Problemrepräsentation
Da (Liu et al., 2014) sicherstellen wollten dass ihr Algorithmus auch sich überschneidende Communities erkennen und wiedergeben kann, haben sie die string-basierte Problemrepräsentation, die wir im Abschnitt Problemrepräsentation erklärt haben, durch eine Mischung einer direkten und indirekten Repräsentation ersetzt, die sie bereits in ihrer Arbeit (Liu et al., 2010) eingeführt haben:
Anstelle der zuvor gestellten Chromosome, welche Mengen von Zahlen waren die die Zugehörigkeit zu Communities repräsentieren, werden Individuen vorgestellt die aus zwei Komponenten bestehen. Die erste Komponente von Individuum \(\mathcal{A}\) ist \(\mathcal{A}\langle P\rangle=\{v_{\pi_1},v,_{\pi_2},\dots,v_{\pi_n}\}\), eine Permutation aller Knoten aus \(V\), wobei \((\pi_1,\pi_2,\dots,\pi_n)\) eben eine Permutation der Zahlen \((1,2,\dots,n)\) ist. Die zweite Komponente von \(\mathcal{A}\) ist \(\mathcal{A}\langle C\rangle\), die Menge der Communities die wir aus \(\mathcal{A}\langle P\rangle\) ziehen können. Dabei ist jedes \(c_i\in\mathcal{A}\langle C\rangle\) die Zahl oder der string der repräsentiert in welcher Community Knoten \(v_i\) liegt. Es ist also \(\mathcal{A}\langle C\rangle\) gerade die zuvor vorgestellten string-basierte Problemrepäresentation, und damit die direkte Darstellung die wir am Ende als Ergebnis ausgeben möchten. Um die indirekte Darstellung \(\mathcal{A}\langle P\rangle\) in \(\mathcal{A}\langle C\rangle\) zu transformieren brauchen wir also einen Dekodierer (Liu et al., 2010).
Decoderfunktion
Um Communities in SNs zu erkennen, erweitern (Liu et al., 2014) das Konzept der Communityfitness auf SNs (Lancichinetti et al., 2009), (Huang et al., 2011) und führen die vorzeichenbehaftete Dichte \(T_{signed}(C)\) ein, die Auskunft über die Qualität einer Community C gibt:
\[T_{signed}(C)=\frac{P_{in}^C-N_{in}^C}{P_{in}^C-N_{in}^C+P_{out}^C}d\]mit
\(P^{C_i}_{in}=\sum_{u,v\in C_i \land (u,v)\in E}\max(s_{signed}(u,v),0)\)
\(P^{C_i}_{out}=\sum_{u\in C_i \land v\in C_j \land i\neq j \land (u,v)\in E}\max(s_{signed}(u,v),0)\)
\(N^{C_i}_{in}=\sum_{u,v\in C_i \land (u,v)\in E}\min(s_{signed}(u,v),0)\)
\(N^{C_i}_{out}=\sum_{u\in C_i \land v\in C_j \land i\neq j \land (u,v)\in E}\min(s_{signed}(u,v),0)\)
Mittels \(T_{signed}(C)\) lässt sich nun innerhalb der Decoderfunktion prüfen, ob Knoten \(v_i\) aus \(\mathcal{A} \langle P \rangle\) zu bisherigen gefundenen Communities \(C=\{C_1,....C_c\}\) gehören könnte: In der Reihenfolge der Permutation \(\mathcal{A} \langle P \rangle\) wird nacheinander für jeden Knoten \(v_i\) folgende Prozedur angewandt: Ist die Ungleichung \(T_{signe}(C_j \cup v_i) > T_{signe}(C_j)\) für jedes \(C_j\in C\) nicht erfüllt, so bildet der Knoten eine neue Community. Ist die Ungleichung erfüllt, wird \(v_i\) den entsprechenden Communities zugeordnet. Im nächsten Schritt wird der folgende Knoten in \(\mathcal{A} \langle P \rangle\) auf gleiche Weise untersucht.
Sollten nach Durchlauf von \(\mathcal{A} \langle P \rangle\) zwei verschiedene Communities mehr als die Hälfte ihrer Knoten teilen, werden solche Communities zusammengeführt.
Zielfunktionen
Um im Evolutionsprozess möglichst gute Communities zu finden, muss der Algorithmus die Communityzuordnung der Knoten dahingehend optimieren, dass positive Kanten in Communities und negative Kanten zwischen Communities verlaufen. Aus diesem Grundsatz leiten sich somit die beiden von (Liu et al., 2014) vorgestellten Zielfunktionen ab, die diese beiden Ziele formalisieren:
\[maximiere f_{pos-in}(C=\{C_1,C_2,...,C_m\})=\frac{1}{m}\sum_{i=1}^{m}\frac{P^{C_i}_{in}}{P^{C_i}_{in}+P^{C_i}_{out}}\]und
\[maximiere f_{neg-out}(C=\{C_1,C_2,...,C_m\})=\frac{1}{m}\sum_{i=1}^{m}\frac{N^{C_i}_{out}}{N^{C_i}_{in}+N^{C_i}_{out}}\]Die Communityzuordnung stellt somit ein Optimierungsproblem mit mehreren Zielen dar (sog. Pareto-Optimierung). MES\(_s\)-SN implementiert diese über den Tchebycheff-Ansatz (Zhang & Li, 2007), der zu folgender Zielfunktion führt:
\[\max\left\{ \lambda_{pos-in}|{f_{pos-in}(C)-f_{neg-out}^{max}}|, \lambda_{neg-out}|{f_{neg-out}(C)-f_{neg-out}^{max}}|\right\}\]wobei \(f_{pos-in}^{max}\) und \(f_{neg-out}^{max}\) das globale Maximum jeweils der \(f_{pos-in}\) und \(f_{neg-out}\) Werte und \((\lambda_{pos-in},\lambda_{neg-out})\) ein Gewichtsvektor darstellen. Hierbei gilt zusätzlich: \(\lambda_{neg-out}=1- \lambda_{pos-in}\) und \(\lambda_{neg-out},\lambda_{pos-in}>0\).
Rekombination und Mutation
Die Rekombinations- und Mutationfunktion sind essentielle Bestandteile eines EAs. Da bei MEA\(_s\)-SN Individuen unter Anderem durch \(\mathcal{A} \langle P \rangle\) dargestellt werden, also Permutationen die Gene bilden, müssen beide Funktionen so gewählt sein, dass die Permutationseigenschaft nicht verletzt wird. Deswegen nutzen (Liu et al., 2014) bei der Erkennung von überlappenden Communities die PMX-crossover Operation, die von (E. Goldberg, 1985) vorgestellt wurde, während die implementierte Mutationsfunktion zufällige Einträge des so entstandenen Genes tauscht. Beide Funktionen bewahren die Permutationseigenschaft.
Der Algorithmus
Input: G = (V, E, w);
Popsize: Anzahl Individuen einer Population;
Popsize Gewichtsvektoren;
T: Anzahl benachbarter Gewichtsvektoren eines Gewichtsvektoren;
Gen: Anzahl Generationen;
Output: Letzte Population;
1: begin
2: Berechne s_signed(u, v) für alle verbundenen Knoten;
3: Berechne euklidische Distanz zwischen zwei Gewichtsvektoren und
bestimme T nächsten Gewichtsvektoren zu jedem Gewichtsvektor;
4: Initialisiere Population in der Form A⟨P⟩;
5: If (suche separierte Communities)
6: Decode A⟨P⟩ zu A⟨C⟩;
7: Initialisiere f_pos_in_max und f_neg_out_max;
8: for i = 1 to Gen do
9: begin
10: for j = 1 to Popsize do
11: begin
12: if (suche separierte Communities)
13: begin
14: Wähle zufälliges Individuum und führe one-way crossover mit A⟨Cij⟩ durch;
15: Führe dichtebasierte Mutation auf A⟨Cij⟩ aus;
16: end;
17: if (suche überlappende Communities)
18: begin
19: Wähle zufälliges Individuum A⟨P⟩ und
Führe PMX crossover operator mit A⟨P_i_j⟩ durch;
20: Führe Mutation auf entstandenes Cild-Individuum aus;
21: end;
22: Update f_pos_in_max und f_neg_out_max;
23: Update Benachbarte Lösungen;
24: end;
25: end;
25: end;
MEA\(_s\)-SN nach (Liu et al., 2014) mit angepassten Bezeichnungen und Formatierung
MEA\(_s\)-SN verlangt neben den Evolutionären Parametern \(Popsize\), \(T\), \(Gen\) eine Menge an \(Posize\) zufälligen Gewichtsvektoren. Diese Gewichtsvektoren beeinflussen über den Tchebycheff-Ansatz, die vom Algorithmus gefundenen Lösungen (Zhang & Li, 2007).
Der Algorithmus startet mit der Berechnung von s_signed(u, v) für alle verbundenen Knoten des Netzwerks G. Es werden die Gewichtsvektoren sortiert und die T nächsten Nachbarvektoren eines Vektors bestimmt. Anschließend wird die Population in der Form \(\mathcal{A} \langle P \rangle\) initialisiert. Es werdem also zufällige Permutationen von allen Knoten des Graphen erzeugt. Um nachfolgend separierte Communities zu erkennen, wird auf alle Individuen \(\mathcal{A} \langle P \rangle\) die vorgestellte Decoderfunktion angewandt, sodass \(\mathcal{A} \langle C \rangle\) bestimmt werden kann. Da \(\mathcal{A} \langle C \rangle\) nicht geeignet ist, um Overlapping Communities darzustellen, wird sowohl \(\mathcal{A} \langle P \rangle\) als auch \(\mathcal{A} \langle C \rangle\) je nach zu erkennenden Community Typ für den evolutionären Prozess genutzt.
Anschließend beginnt der evolutionäre Part von MEA\(_s\)-SN und für jede Generation werden folgende Schritte für alle Individuen der Population angewandt: Werden separierte Communities gesucht, so wird ein Individuum A in der Darstellung \(\mathcal{A} \langle C \rangle\) betrachtet. Hierauf wird die one-way-crossover Operation mit einem zufälligen anderen Individuum ausgeführt und das so entstandene Kindindividuum anschließend nochmals in Abhängigkeit der Dichte mutiert. Werden überlappende Communities gesucht, so wird ein Individuum A in der Darstellung \(\mathcal{A} \langle P \rangle\) betrachtet. Auf \(\mathcal{A} \langle P \rangle\) wird die PMX-crossover Operation mit einem zufälligen anderen Individuum angewandt und das entstandene Ividuum mittels swap-Operation mutiert. Unabhängig vom zu erkennenden Community-Typ, wird das so entstandene Kindindividuum mit jeden der T Nachbarknoten des ursprünglichen Individuums nach dem bereits vorgestellten Tchebycheff-Ansatz verglichen. Wird hierbei die Zielfunktion verbessert, wird das (Nachbar-)Individuum durch das Kindindividuum ersetzt.
Nachdem Gen Generationen berechnet wurden, terminiert MEA\(_s\)-SN und gibt Popsize mögliche Lösungen (Communitystrukturen) aus.
Memetic Algorithm for Community Detection in Signed Networks (MACD-SN)
Memetische Algorithmen basieren auf Populationsansätzen der Natur. Hinsichtlich dieser Art von Algorithmen besteht das Grundprinzip darin ein Problem zu lösen, indem man mithilfe einer lokalen Änderung der aktuellen Lösung eine bessere Lösung aus der gerade betrachteten Nachbarschaft findet. Die betrachtete Problemstellung löst man, indem man zunächst das Problem in einem unmittelbaren minimalen Bereich löst. Sukzessiv wiederholen sich diese Schritte bis sich ein Cluster Network bildet. Im Zuge dessen durchläuft \(MACD-SN\) mehrere Schleifen. Um eine bestmögliche Laufzeit zu erreichen, wird bei \(MACD-SN\) vorerst das Netzwerk initialisiert.
Mithilfe der Initialisierung sollen die Initialbesetzung der Chromosome gesetzt werden. Ad hoc definiert man den Node Imbalance Degree (\(NID\)):
\[NID(v_i,c)=\sum_{v_j \in c \wedge (v_i,v_j) \in E \wedge A_ij=-1 } |A_{i,j}| +\sum_{v_j \notin c \wedge (v_i,v_j) \in E \wedge A_ij=1 } |A_{i,j}|\]Je höher \(NID(v_i,c_s)\) ist, desto unpassender wäre \(v_i\) in \(c_s\). Folglich falls \(NID(v_i,c_1)< NID(v_2,c_s)\), erhielte \(c_1\) eine höhere Priorität als \(c_2\) während der Zuordnung in Communities. Der darauffolgende Algorithmus 1 ermittelt die Initialbesetzung der Chromosome in \(popu\):
Algorithmus 1
Algorithmus Input: Eine Matrix G als vorzeichenbehafteten Graphen;
ALgorithmus Output: Initialbesetzung der Chromosomen;
1: for j = 1 to popu_size do
2: for k = 1 to n do
3: popu[j][k] = A random integer in the range of 1 to n generated randomly;
#popu[] is an array
#of chromosomes population. popu[j][k]
#represents the kth gene of the jth
#chromosome.
4: end for
5: flag = 1;
6: while flag do
7: flag = 0;
8: for k = 1 to n do
9: comms = The set of communities to which
the neighbor nodes of node k belong;
10: t = ∞;
11: m = popu[j][k];
12: for each community comm ∈ comms do
13: if NID(k, comm) < t then
14: t = NID(k, comm);
15: m = comm;
16: end if
17: end for
18: if m 6= popu [j] [k] then
19: popu[j][k] = m;
20: flag = 1;
21: end if
22: end for
23: end while
24: end for
25: return popu[];
Initialisierung von MACD-SN nach (Che et al., 2020) mit angepassten Formatierung (Pseudocode)
Drei wesentliche Schleifen dominieren den Algorithmus. Die Iteration durch die Genen in einem Chromosom geschieht in dem Bereich von Codezeile 1 bis Codezeile 4. Zusätzlich ordnet man jedem \(popu[j][k]\) (den k-ten Gen im j-ten Chromosom) einen zufälligen Wert zwischen \(1\) und \(n\) zu. Die Codezeilen von 5 bis 17 prüfen für welche Communities der Nachbarn \(popu[j][k]\), der \(NID(k, comm)\) am minimalsten ist. Die Community, die den minimalsten \(NID\) Wert bezüglich \(popu[j][k]\) besitzt, wird \(popu[j][k]\) als Community zugeordnet. Aufgrund der Schleife in der Codezeile 1 werden die oben genannten Schritte für jedes Chromosom in popu wiederholt.
Ein weiterer elementarer Aspekt ist die Fitness Funktion. Je höher der Wert ist, desto “besser” sind die Community Partitionen. Die Fitness Funktion wird wie folgt berechnet.
\[Q_s=\frac{1}{2a^+ +2a^-}\sum_i\sum_j[A_{ij}-(\frac{a^+_i a^+_j}{2a^+} -\frac{a^-_i a^-_j}{2a^-})]\delta (c_i,c_j)\]Hierbei geben \(a^+_i\) und \(a^-_i\) die totale Anzahl der positiven beziehungsweise negativen Kanten des Knoten \(v_i\) an.
Operatoren
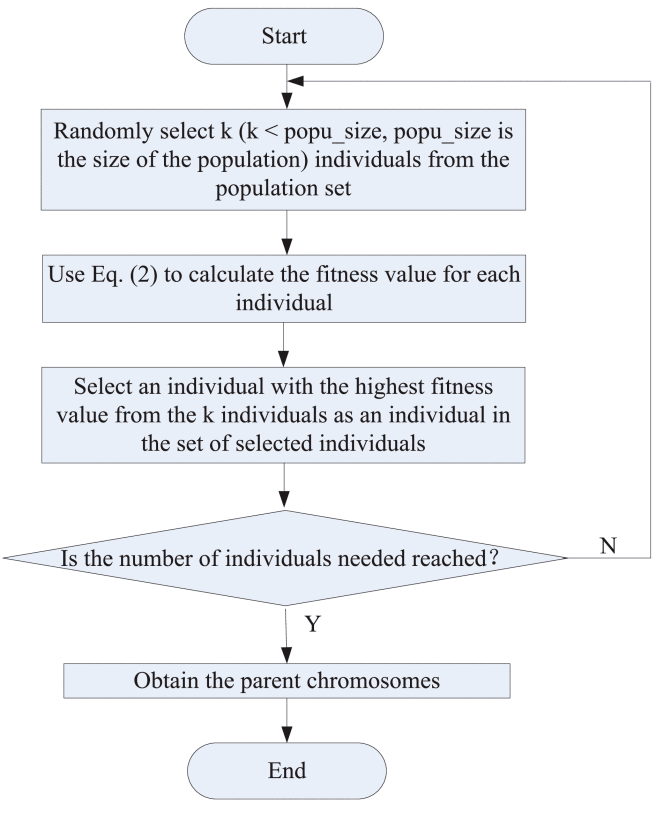
Selection, Crossover, und Mutation sind die drei fundamentale Operatoren für memetische Algorithmen. Beruhend auf (Che et al., 2020) wird Tournament selection als Selection Operator verwendet. Mithilfe der Fitness Funktion ermittelt Tournament selection die Eltern Chromosome. Das folgende Flussdiagramm (Abb. 3) fasst die essenziellen Handlungen des Tournament selection Algorithmus zusammen.
 |
 |
| Abbildung 3: Flussdiagramm des Tournament selection Algorithmus (Che et al., 2020) |
Abbildung 4: Beispiellauf des Crossover Operator (Che et al., 2020) |
Der Crossover Operator arbeitet mit den Resultaten der Selection Operatoren weiter. Simultan läuft auf zwei verschiedenen Eltern Chromosomen die Anwendung des Crossover Algorithmus. Fundiert auf der genetischen Kreuzung der Biologie entstehen anhand des Algorithmus neue einzigartige Chromosome.
- Alle Komponenten aus \(ch_1\) und \(ch_2\) werden als unberührt initialisiert.
- Ein zufälliges \(r\) wird generiert.
- Unberührte Komponente in einem Chromosom abhängig von r wählen.
- Alle Komponenten mit dem selben Komponenten Wert ebenfalls auswählen.
- Den aktuellen \(c_t\) Wert in individuellen descendant (\(d_{c_t}\)) speichern.
- Erhöhe \(c_t\) um 1 und markiere alle ausgewählten Komponenten als berührt.
- Wiederhole 1-6 bis alle descendant\(\neq 0\) sind
(1) bis (7) setzen den Crossover Algorithmus zusammen.
Der letzte Operator soll die individuellen Eltern Chromosome verfeinern. Aus Algorithmus 2 lässt sich entnehmen, dass zu jeder Community der größte zugehörige \(CID(comm)\) gespeichert wird. Community Imbalance Degree (CID) bildet sich aus :
\(CID(comm)=\frac {1}{n_C}\sum_{v_i\in comm} NID(v_i,comm)\) , hierbei verkörpert \(n_C\) die Anzahl der Knoten in der Community \(comm\).
Die Kernessenz der Formel lautet: Je höher \(CID(comm)\) ist, umso evidenter ist die Cluster Struktur der Community \(comm\). Falls der größte \(CID(comm)\) Wert größer als der Parameter \(\delta\)und m \(\neq 0\) ist, dann wählt man einen Knoten \(v_s \in ns\). Von diesem Knoten wird ein positiver Nachbar gewählt, welcher sich nicht in der homogenen Community von \(v_s\) befindet. In den Schlusszeilen des Algorithmus setzt man das Eltern Chromosom des Knoten \(v_s\) auf dem Eltern Chromosom des gefundenen Knoten. Von Codezeile 19 bis 25 überprüft der Algorithmus, ob \(Q_s\) mit \(H_{neu}\)>\(Q_s\) mit \(H\) ist. Falls die if-Bedingung in Codezeile 21 wahr ist, wird \(H_{neu}\) zurückgegeben.
Algorithmus 2
Algorithmus Input: Eine Matrix G als vorzeichenbehafteten Graphen;
ALgorithmus Output: Verbesserte Eltern Chromosome H;
1: comms = The set of clusters in H;
2: k = −∞;
3: m = 0;
4: for each cluster comm ∈ comms do
5: if CID(comm) > k then
#CID (comm) is the community
#imbalance degree of community comm.
6: k = CID(comm);
7: m = comm;
8: end if
9: end for
10: if m != 0 && CID(m) > δ then
11: ns = All vertices in m;
12: Hneu= H;
13: while every vertex vs∈ns do
14: Stochastically choose a positive neighbour vt of
vertex vs (vs and vt are not included in the
identical cluster);
15: if there is vt satisfying the condition then
16: Hneu[vs] = Hneu[vt];
17: end if
18: end while
19: qsH = Qs value of H computed using formula (2);
20: qsHneu = Qs value of Hneu computed using formula (2);
21: if qsHneu > qsH then
22: return Hneu;
23: end if
24: end if
25: return H;
Mutation-Operator nach (Che et al., 2020) mit angepassten Formatierung (Pseudocode)
Lokale Suchfunktion
Für memetische Algorithmen sind lokale Suchfunktionen von notwendiger Bedeutung. Mittels gut ausgearbeiteten lokalen Suchfunktionen steigt die Genauigkeit vehement. Der vorgestellte Algorithmus orientiert sich an (Che et al., 2020). Die wesentliche Aufgabe des Algorithmus besteht darin, die beste Community für Knoten \(i\) zu ermitteln. Der lokale Faktor bezieht sich auf den Suchbereich.
Der beste individuelle Nachwuchs in einem Nachwuchs Set und der Parameter \(p\) sind die Inputs des Algorithmus. Zunächst wird die Liste an Communities \(comms\) auf \(\varnothing\) gesetzt. Nun befüllt der Algorithmus \(comms\) mit den neuen gebildeten Communities, welche die meisten positiven Nachbarn des Knoten \(i\) haben (Mehrere Communities erfüllen die Bedingung). Dabei werden zwei Fallunterscheidungen beachtet:
1.Fall: \(comms\neq\varnothing\) nach Befüllung
Der kleinste \(CID\) Wert bezüglich \(comms\) mit \(i\) wird bestimmmt. Die Community mit dem kleinsten \(CDI\) speichert der Algorithmus in m.
2.Fall: \(comms=\varnothing\) nach Befüllung(\(i\) hat nur negative Kanten zu sich)
\(comms\) wird mit den Communities der negativen Nachbarn von \(i\) gefüllt und die Community bezüglich \(i\) mit den kleinsten \(CID\) speichert der Algorithmus in m.
Im letzten Schritt fügt man \(i\) des besten Nachwuchses in der Community \(m\) ein. Man berechnet die Fitness des individuellen besten Nachwuchs und des neuen erstellten besten Nachwuchs. Die Rückgabe des Algorithmus ist der neu erstellte beste Nachwuchs, falls die Fitness des neuen erstellten besten Nachwuchses größer ist als die Fitness des individuellen besten Nachwuchses oder falls die zufällig generierte Zahl kleiner als das gegebene \(p\) ist.
MACD-SN Algorithmus
MACD-SN formiert sich aus allen oben genannten Algorithmen beziehungsweise Funktionen zusammen. Zu Beginn des Codes kalkuliert man \(Q_S\) für jedes Individuum (Chromosom) von popu die Fitness, darauf folgt die Bestimmung der Eltern Chromosomen mithilfe von der tournament selection. Die identische Anzahl an Eltern Chromosome werden zufällig aus popu ausgewählt und mit diesen Elementen wird ein Max-Heap gebildet. Das Element in der Wurzel des Max-Heap speichert der Schritt in \(offs[i]\) (\(i\) ist die Wurzel des Max-Heaps). Die Codezeilen 10 bis 25 simulieren die Zufallsaktionen innerhalb der Genetik der Biologie. Mit einer gewissen Wahrscheinlichkeit tritt der Crossover Operator zwischen \(offs[i]\) und \(offs[i+1]\) ein und mit einer anderen(oder gleichen) Wahrscheinlichkeit tritt der Mutation Operator ein. Das Individuum mit der höchsten Fitness wird als bestOffstring festgehalten und mit als Parameter in die lokale Suche gegeben. Die Rückgabe der lokalen Suche ist der überarbeitete bestOffstring. In Codezeile 28 addiert man \(offs + bestOffstring\) zu popu hinzu. Diese Schritte geschehen so oft bis \(gt\) mal keine Verbesserung durch diese Schritte erreicht wurden. Dadurch dass popu mit popu_size initialisiert ist, befinden sich im Set von den ersten popu_size Individuen genau die Partition mit der höchsten Fitness.
Algorithm 3 (MACD-SN)
Algorithm Parameters:
popu_size: Populationsgröße ;
k: Anzahl an Eltern Chromosome, die mithilfe von tournament selection gewählt wurden;
p1: Crossover operator Wahrscheinlichkeit;
p2: Traditionelle mutation operator Wahrscheinlichkeit;
p3: Community mutation operator Wahrscheinlichkeit;
δ: Parameter in Community mutation operator;
p: Parameter in der Funktion LocalSeek() (lokale Suche);
gt: maximale Menge an Wiederholungen ohne Veränderungen;
Algorithm Input: Eine Matrix G als vorzeichenbehafteten Graphen;
Algorithm Output: Eine Cluster Partition comms des vorzeichenbehafteten Graphen;
1: #produce initial individual population
popu = initialize(popu_size);
2: repeat
3: Use formula (2) to compute the fitness function
value of every individual in the population popu;
4: for i = 1 to k do
#Using tournament selection algorithm to select parent individuals for
#subsequent genetic operations.
5: Randomly select k individuals from the population set popu;
6: Using the selected k individuals to build a maximum heap;
7: offs[i] = The top element of the maximum heap;
#offs[] is a individuals set selected for
#subsequent genetic operations.
8: end for
9: i = 1;
10 while i ≤ k-1 do
11: if rand(0,1) ≤ p1 then
12: (offs[i], offs[i+1])=Crossover(offs[i], offs[i+1]);
#Perform a randomized two-way crossover
#operation. The Crossover function returns
#two individuals, offs[i] and offs[i + 1].
13: end if
14: i = i + 2;
15: end while
16: for i = 1 to k do
17: if rand(0,1) ≤ p2 then
18: offs[i] = The traditional mutation operator is executed on the offs[i];
19: end if
20: end for
21: for i = 1 to k do
22: if rand(0,1) ≤ p3 then
23: offs[i] = CommunityMutation(offs[i], δ);
#The community mutation operator is executed
#on the offs[i];
24: end if
25: end for
26: bestOffspring = The individual with the maximum fitness function value in offs;
27: bestOffspring = LocalSeek(bestOffspring, ρ);
28: popu = popu + offs + bestOffspring;
29: popu = The set of the first popu_size individuals
with the largest fitness in the population popu;
30: until (no improved amount of iterations for the
optimal individual in population popu >= gt);
31: comms = Cluster partition of individual with the
biggest fitness function value in the population popu;
32: return comms;
MACD-SN nach (Che et al., 2020) mit angepassten Formatierung (Pseudocode)
Resultat und Diskussion
In dieser Arbeit haben wir die genaue Funktionsweis zweier Evolutionäre Algorithmen für die Communityerkennung in Netzwerken mit vorzeichenbehafteten Kanten vorgestellt.
Hierbei zeichnet sich MEA\(_s\)-SN dadurch aus, sowohl für das Erkennen separierter als auch überlappender Communities verwendet werden zu können. Die Zeitkomplexität von des Algorithmus beträgt nach den Autoren \(O(Gen×Popsize×n)\) für dem evolutionären Teilalgorithmus und \(O(Popsize×n^2)\) für den Preprozessingabschrit. Somit lässt sich die Gesamtlaufzeit zu \(O(Gen×Popsize×n+Popsize×n^2)\) abschätzen. MACD-SN ist Im Gegensatz MEA\(_s\)-SN nicht in der Lage, überlappende Communities zu erkennen, wobei die Autoren diese Problem in Zukunft lösen wollen. Als Laufzeit geben die Autoren \(O(Popsize×k×m×n+Popsize×n^2)\) an, wobei \(O(Popsize^2)\) als Laufzeit des Initiierungsschritt aufgeführt wird. Im Laufzeitverhalten unterscheiden sich die beiden Algorithmen somit kaum. Lediglich terminiert MACD-SN bereits, wenn automatisch wenn fortlaufend keine Verbesserung der Fitnessfunktion mehr stattfindet, während MEA\(_s\)-SN alle \(Gen\) Generationen berechnet.
Abschließend lässt sich festhalten, dass EAs sich auch für die Communitierkennung in vorzeichenbehafteten Netzwerken eignen.
Referenzen
- Liu, C., Liu, J., & Jiang, Z. (2014). A multiobjective evolutionary algorithm based on similarity for community detection from signed social networks. IEEE Transactions on Cybernetics, 44(12), 2274–2287. https://doi.org/10.1109/TCYB.2014.2305974
- Liu, J., Zhong, W., Abbass, H. A., & Green, D. G. (2010). Separated and Overlapping Community Detection in Complex Networks using Multiobjective Evolutionary Algorithms. 2010 IEEE Congress on Evolutionary Computations (CEC), -.
- Che, S., Yang, W., & Wang, W. (2020). A Memetic Algorithm for Community Detection in Signed Networks. IEEE Access, 8, 123585–123602. https://doi.org/10.1109/ACCESS.2020.3006108
- Tasgin, M., Herdagdelen, A., & Bingol, H. (2007). Community Detection in Complex Networks Using Genetic Algorithms. http://arxiv.org/pdf/0711.0491v1
- Shi, C., Yan, Z., Cai, Y., & Wu, B. (2012). Multi-objective community detection in complex networks. Applied Soft Computing, 12(2), 850–859. https://doi.org/10.1016/j.asoc.2011.10.005
- Huang, J., Sun, H., Liu, Y., Song, Q., & Weninger, T. (2011). Towards online multiresolution community detection in large-scale networks. PloS One, 6(8), e23829. https://doi.org/10.1371/journal.pone.0023829
- Easley, D., & Kleinberg, J. M. (2010). Networks, Crowds, and Markets - Reasoning About a Highly Connected World. Cambridge.
- Tang, J., Lou, T., & Kleinberg, J. (2012). Inferring social ties across heterogenous networks. In E. Adar (Ed.), Proceedings of the fifth ACM international conference on Web search and data mining (p. 743). ACM. https://doi.org/10.1145/2124295.2124382
- Lancichinetti, A., Fortunato, S., & Kertész, J. (2009). Detecting the Overlapping and Hierarchical Community Structure in Complex Networks. New J Phys (New Journal Of Physics), 11(3), 033015. https://doi.org/10.1088/1367-2630/11/3/033015
- Zhang, Q., & Li, H. (2007). MOEA/D: A Multiobjective Evolutionary Algorithm Based on Decomposition. IEEE Transactions on Evolutionary Computation, 11(6), 712–731. https://doi.org/10.1109/TEVC.2007.892759
- E. Goldberg, R. L. (1985). Alleles, loci, and the traveling salesman problem. In Proceedings of the first International Conference Genetic Algorithms (pp. 154–159).