Berechnung der strukturellen Ausgeglichenheit in vorzeichenbehafteten Netzwerken
| Darya Naumava | Patrick Frank | ||
|---|---|---|---|
| RWTH Aachen University | RWTH Aachen University | ||
| darya.naumava@rwth-aachen.de | patrick.frank@rwth-aachen.de |
Abstract
Durch die Digitalisierung und das Internet hat die Vernetzung von Nutzern eine hohe Bedeutung gewonnen. Denn eine gute Vernetzung von Nutzern oder Mitgliedern bedeutet für viele Unternehmen oder Organisationen langfristige Vorteile. Beispielsweise in Form einer höheren Bindung der Nutzer an das Unternehmen oder der Mitglieder an die Organisation. Allerdings stellt die Bewertung solcher Netzwerke hinsichtlich der Harmonie von Beziehungen eine Herausforderung dar. Erstens, weil es zu bewerten gilt, ob unterschiedliche Beziehungen zwischen zwei oder mehr Personen harmonisch oder unausgeglichen sind. Und zweitens, weil die Entdeckung von Gemeinschaften in großen Netzwerken selbst mit geeigneten Algorithmen eine Herausforderung darstellt. Die Untersuchung der Zyklen stellt dabei einen vielversprechenden Ansatz dar, um Rückschlüsse über die Balance eines Netzwerkes zu erhalten. Die Ausgeglichenheit wird dabei berechnet, indem einzelne Zyklen entdeckt und auf ihre Balance geprüft werden, sodass Aussagen über das Maß der Balance eines gesamten Netzwerkes getroffen werden können. Durch geeignete Anwendungsbeispiele wird ersichtlich, dass eine Anwendung dieser Methode auf kleine bis große Netzwerke möglich und zielführend ist. Dementsprechend können mithilfe dieses Ansatzes effiziente Analysen von vorzeichenbehafteten Netzwerken durchgeführt werden, die es Unternehmen und Organisationen ermöglicht, eine kostengünstige und detaillierte Auskunft über die Ausgeglichenheit der Beziehungen ihrer Kunden oder Mitglieder zu erhalten.
Inhaltsverzeichnis
1. Einleitung
Die strukturelle Ausgeglichenheit ist ein Teilgebiet der Graphen- und Netzwerkanalyse und gibt eine Auskunft über die Balance der Beziehungen in einem vorzeichenbehafteten Netzwerk. Die Analyse von Zyklen stellt dabei einen Ansatz zur Bewertung der strukturellen Ausgeglichenheit dar.
Dabei liefert das Maß der Balance signifikante Informationen und Erkenntnisse, um die Vernetzung zwischen Nutzern oder Mitgliedern in Netzwerken oder Gemeinschaften zu bewerten sowie zu verbessern. Denn mithilfe der gewonnenen Informationen wird es Entscheidungsträgern ermöglicht, die Beziehungen in einem Netzwerk oder einer Gemeinschaft besser zu beurteilen sowie einzuschätzen. Somit können beispielsweise fundierte Entscheidungen hinsichtlich dem Kommunikationsdesign für webbasierte Anwendungen getroffen werden, die eine höhere Zufriedenheit und Bindung der Nutzer oder der Mitglieder zur Folge haben können.
Die Analyse von Zyklen ermöglicht es dabei, bestehende vorzeichenbehaftete Netzwerke auf effiziente Weise zu analysieren und aus den gewonnenen Informationen, Rückschlüsse über das Maß der strukturellen Ausgeglichenheit zu ziehen. Dies ist signifikant, weil die Untersuchung der Zyklen eine kostengünstigere Variante zur Bewertung der Balance darstellt sowie die Möglichkeit bietet, eine schnelle Auskunft über die Harmonie einer Gemeinschaft oder eines Netzwerkes zu erhalten. Dementsprechend sind dieser Ansatz von praktischer Relevanz und die gewonnenen Erkenntnisse hinsichtlich der Analyse von Zyklen zur Berechnung der Balance von Bedeutung.
Der wissenschaftliche Beitrag der Arbeit besteht darin, eine Übersicht über die Analyse von Zyklen zur Berechnung der strukturellen Ausgeglichenheit bereitzustellen sowie geeignete Formeln für die Analyse von Zyklen in kleinen und großen vorzeichenbehafteten Netzwerken vorzustellen und anzuwenden. Darüber hinaus werden die unterschiedlichen Formeln in Hinblick auf deren Einsatzbereich verglichen.
Zu Beginn werden hierbei die Grundlagen vorzeichenbehafteter Graphen erläutert und die strukturelle Ausgeglichenheit von Triaden und Zyklen unterschiedlicher Länge untersucht. Diesen Ergebnissen folgend werden Formeln für die Berechnung der strukturellen Ausgeglichenheit eingeführt sowie diese auf unterschiedliche Netzwerke in vorzeichenbehafteten Graphen angewendet, um die Balance zu ermitteln. Darüber hinaus werden die resultierenden Formeln und Erkenntnisse am Beispiel der Datensätze von Epinions, Slashdot und Wikipedia angewendet. Die Analyse macht dabei insbesondere von Methoden der Graphentheorie und Statistik Gebrauch. Alles in allem sollen somit Erkenntnisse über die Berechnung der strukturellen Ausgeglichenheit in vorzeichenbehafteten Netzwerken gewonnen werden, die für die effiziente Bewertung gleichartiger Netzwerke genutzt werden können.
2. Verwandte Arbeiten
Für die Berechnung der Harmonie von vorzeichenbehafteten Netzwerken findet sich eine Vielzahl an vergangenen sowie aktuellen Forschungsarbeiten. Im Folgenden werden vier verwandte Arbeiten wiedergegeben, die in ihrem Beitrag die Analyse mithilfe von Zyklen zur Berechnung der Balance beschreiben oder aufgreifen. Abschließend werden die entscheidenden Abgrenzungen zu dem vorliegenden Beitrag dargestellt.
Hierbei gibt die erste, der verwandten Arbeiten, eine Übersicht hinsichtlich der wissenschaftlichen Aktivitäten zur Berechnung der Balance, wobei darüber hinaus eine Abgrenzung des vorliegenden Beitrages stattfindet. Bei den nachfolgenden drei verwandten Beiträgen werden die Analyseansätze des jeweiligen Beitrages beschrieben sowie wird anschließend verglichen, inwiefern sich die vorliegende Arbeit abgrenzt.
Einen Überblick über die wissenschaftlichen Aktivitäten zur Berechnung der strukturellen Ausgeglichenheit gibt der Beitrag von Zheng, X., Zeng, D. und Wang, F.-Y. (Zheng et al., 2015). Dabei werden die grundlegenden Konzepte sowie Methoden zur Bestimmung der Balance vorgestellt sowie miteinander verglichen. Ein Bestandteil, der vorgestellt und behandelt wird, ist die Berechnung der Balance mithilfe von Zyklen. Des Weiteren werden ebenfalls mehrere bestehende Probleme, die bei Untersuchung der strukturellen Ausgeglichenheit noch nicht zufriedenstellend gelöst sind, diskutiert. Die Abgrenzung zur vorliegenden Arbeit besteht darin, dass Zheng, X., Zeng, D. und Wang, F.-Y. einen weitläufigeren Überblick über mehrere Methoden zur Berechnung der Balance geben, wobei die Berechnung der strukturellen Ausgeglichenheit mittels Zyklen lediglich in kleinem Umfang beschrieben wird. Dementsprechend liefert der vorliegende Beitrag detailliertere Informationen und mehrere Formeln zur zyklusbasierten Analyse und Berechnung der Balance von Netzwerken sowie ausführlichere Anwendungsbeispiele für die Bestimmung der zyklusbasierten Balance.
Die Arbeit von Aref, S. und Wilson, M. C. (Aref & Wilson, 2018) zeichnet sich aus, indem diese verschiedene Arten von Teilnetzwerken mithilfe unterschiedlicher Berechnungsansätze auf ihre Balance untersucht und die Methoden miteinander vergleicht. Die Berechnungsmethoden basieren dabei insbesondere auf der Untersuchung von Zyklen sowie auf der Berechnung der Balance basierend auf Eigenwerten und der Frustration in Teilgraphen. Dabei zeigen die Ergebnisse, dass bei zyklusbasierten, Eigenwert-basierten und Frustration-basierten Methoden unterschiedliche Niveaus der Balance in einem Netzwerk beobachtbar sind. Die Abgrenzung zum vorliegenden Beitrag besteht darin, dass die Arbeit von Aref, S. und Wilson, M. C. die verschiedenen Berechnungsmethoden in Abhängigkeit von unterschiedlichen Graphen untersucht. Die vorliegende Arbeit legt den Schwerpunkt ausschließlich auf die Analyse von Zyklen und untersucht die Anwendung der unterschiedlichen zyklusbasierten Berechnungsansätze und Formeln auf vorzeichenbehaftete Netzwerke, um eine verlässliche Aussage über das Maß der strukturellen Ausgeglichenheit zu bekommen. Zudem verfolgt der vorliegende Beitrag das Ziel, den zyklusbasierten Ansatz auf große Netzwerke anzuwenden.
Der Beitrag von Kirkley, A., Cantwell, G. T. und Newman, M. E. J. (Kirkley et al., 2019) untersucht die Balance basierend auf der Analyse von Pfaden entlang der Kanten in dem Netzwerk und berechnet diese, um die strukturelle Ausgeglichenheit zu bestimmen. Dabei werden unterschiedliche Ansätze, wie beispielsweise zyklusbasierte Ansätze, hinsichtlich der Methode der Pfad-Analyse eingeführt und die Resultate verglichen. Zudem wird festgestellt, dass unbekannte Zeichen in ansonsten bekannten, vollständig beschrifteten Netzwerken vorhersagbar sind, indem die Balance maximiert wird. Die Abgrenzung zum vorliegenden Beitrag besteht darin, dass Kirkley, A., Cantwell, G. T. und Newman, M. E. J. zur Berechnung der strukturellen Ausgeglichenheit zyklusbasierte Ansätze einführen, aber die Analyse von Pfaden zur Bestimmung der strukturellen Ausgeglichenheit priorisieren, wobei die vorliegende Arbeit die Analyse von Zyklen zur Bestimmung der Balance in den Vordergrund stellt und die Erkenntnisse auf repräsentative Beispiele anwendet.
Die Arbeit von Aref, S. und Wilson, M. C. (Aref & Wilson, 2019) beschreibt die Berechnung der Frustration durch die Untersuchung der Anzahl von negativen Kanten innerhalb von Pfaden oder Zyklen in einem Netzwerk. Dabei stellt der Beitrag allgemeine Methoden zur Berechnung der strukturellen Ausgeglichenheit in vorzeichenbehafteten Netzwerken und Teilnetzwerken vor. Zudem werden diese Methoden auf eine Reihe repräsentativer Beispiele angewendet. Der Frustrationsindex ist hierbei ein Schlüsselmaß für die Analyse von vorzeichenbehafteten Netzwerken und gibt eine Auskunft über die Balance eines Netzwerkes. Die Abgrenzung zum vorliegenden Beitrag besteht darin, dass sich Aref, S. und Wilson, M. C. verstärkt dem Frustrationsindex widmen und die vorliegende Arbeit sich auf die Analyse der Zyklen zur Berechnung der strukturellen Ausgeglichenheit in vorzeichenbehafteten Netzwerken konzentriert.
3. Hintergrundwissen und Eingrenzungen
Im Folgenden werden die wichtigsten und grundlegenden Begriffsdefinitionen geklärt sowie Eingrenzungen dieser Arbeit definiert.
Netzwerke und Graphen:
Ein Netzwerk ist eine Ansammlung von Punkten, die paarweise durch Linien verbunden sind. Diese Punkte werden als Knoten und die Linien als Kanten bezeichnet. Dabei lassen sich viele Beziehungen aus unterschiedlichen wissenschaftlichen Bereichen wie der Physik, Biologie und Sozialwissenschaft mit Netzwerken darstellen (Newman, 2018).
Ein Netzwerk kann in grafischer Form als Graph dargestellt werden.
Vorzeichenbehaftete Netzwerke und Graphen:
In der vorliegenden Arbeit werden vorzeichenbehaftete Netzwerke als eine Erweiterung von Netzwerken gesehen, die zusätzliche Informationen über positive und negative Relationen enthalten und sich als vorzeichenbehaftete Graphen darstellen lassen. Dabei repräsentieren Knoten Personen und Kanten stellen symmetrische Beziehungen zwischen Personen dar, wobei jede Kante als positiv oder negativ in Abhängigkeit von der Art der Beziehung (freundlich oder feindselig) bezeichnet wird (Cartwright & Harary, 1956).
Behandlung fehlender Kanten:
Hinsichtlich dem Ignorieren fehlender Kanten oder der Interpretation fehlender Kanten als negative Kanten, finden sich widersprüchliche Sichtweisen. Die vorliegende Arbeit ignoriert fehlende Kanten und behandelt diese nicht gesondert, um mögliche, daraus resultierende, fehlerhafte Interpretationen oder Ergebnissen für das Maß der strukturellen Ausgeglichenheit zu vermeiden (Tang et al., 2015).
Zyklen höherer Ordnung:
Ein Zyklus höherer Ordnung ist definiert durch eine Menge von drei oder mehr Knoten, bei denen jeder Knoten innerhalb des Zyklus mit genau zwei anderen Knoten des Zyklus verbunden ist. Hat ein Knoten drei oder mehr Kanten innerhalb eines Zyklus, wird nicht mehr von einem Zyklus, sondern von einem Netzwerk gesprochen. Dementsprechend ist es notwendig, wenn ein Netzwerk mindestens einen Knoten mit drei oder mehr Kanten enthält, dieses Netzwerk weiter aufzuteilen, bis nur Zyklen übrig sind, die der definierten Bedingung genügen. Denn nur Zyklen mit Knoten, die genau zwei Kanten haben, können mathematisch auf ihre Balance untersucht werden (Chiang et al., 2013).
Demzufolge werden die Dyade (Beziehung zwischen genau 2 Knoten) sowie der verbindungslose Knoten innerhalb dieser Arbeit vernachlässigt und die Berechnung der strukturellen Ausgeglichenheit an der Analyse von Zyklen höherer Ordnung orientiert. Dieser Eingrenzung entsprechend wird im Folgenden „Zyklus“ als Synonym für „Zyklus höherer Ordnung“ verwendet.
Zudem gilt stets, dass jeder Zyklus ein Netzwerk ist, aber nicht jedes Netzwerk ein Zyklus, weil ein Netzwerk aus mehreren Zyklen bestehen kann.
Vollständige Verknüpfung von Zyklen:
In Übereinstimmung mit dem Ignorieren fehlender Kanten werden innerhalb dieser Arbeit lediglich vollständig verknüpfte Zyklen betrachtet, bei denen alle Kanten existieren, und unvollständig verknüpfte Zyklen vernachlässigt.
Synonyme Begriffsverwendungen für strukturelle Ausgeglichenheit:
Die Begriffe „strukturelle Ausgeglichenheit“, „Balance“, „Positiver Zyklus“, „Harmonie“ sowie „strukturell ausgeglichen sein“, „balanciert sein“, „positiv sein“ und „harmonisch sein“ werden im Folgenden als Synonyme verwendet.
Definition großer Netzwerke:
Innerhalb der Arbeit wird der Begriff „großes Netzwerk“ verwendet, wobei ein großes Netzwerk als ein Netzwerk mit mindestens \(5.000\) Knoten definiert ist.
4. Methodik
Zu Beginn werden die k-Zyklen sowie deren Kriterien für die strukturelle Ausgeglichenheit betrachtet. Darauf folgend werden in Kapitel 4.2 drei Formeln für die Berechnung der Balance in vorzeichenbehafteten Netzwerken vorgestellt.
4.1. k-Zyklen und strukturelle Ausgeglichenheit
Mit k-Zyklen werden alle Zyklen der Kantenzahl \(k\) beschrieben.
Als allgemeingültiges Kriterium für die strukturelle Ausgeglichenheit gilt, dass ein Zyklus mit Kantenzahl \(k\) balanciert ist, wenn die Anzahl der negativen Kanten durch zwei teilbar ist oder alle Kanten positiv sind. Andernfalls gilt ein Zyklus als unausgeglichen, wenn die Anzahl der negativen Kanten innerhalb des Zyklus ungerade ist (Cartwright & Harary, 1956).
Dabei können die Kanten in dem Zyklus in beliebiger Reihenfolge angeordnet werden, sodass für jede Vorzeichenkonstellation mehrere Anordnungen existieren können. Maßgeblich für die strukturelle Ausgeglichenheit ist ausschließlich die Anzahl der negativen Vorzeichen in dem Zyklus, wobei die Anordnung der Vorzeichen für die Bestimmung der Balance unberücksichtigt bleibt. Dies gilt für alle k-Zyklen (Doreian & Mrvar, 1996).
Als Beispiel werden im Folgenden für eine ungerade Anzahl an Kanten die 3-Zyklen und für eine gerade Anzahl an Kanten die 4-Zyklen vorgestellt.
Tabelle 1: Balancierte und nicht balancierte 3-Zyklen
| \(\) 3-Zyklus \(\) | |
|---|---|
| \(\) \(+ + +\) | \(\) balanciert \(\) |
| \(\) \(+ - -\) | \(\) balanciert \(\) |
| \(\) \(+ + -\) | \(\) nicht balanciert \(\) |
| \(\) \(- - -\) | \(\) nicht balanciert \(\) |
Bei den Triaden, dem 3-Zyklus, in Tabelle 1 handelt es sich um den kleinstmöglichen Zyklus (gemäß Definition aus Kapitel 3), mit drei Knoten und drei Kanten. Dabei sind die Kanten entweder mit einem positiven oder negativen Vorzeichen beschriftet (Chiang et al., 2013). Nach Heider’s Theorem ist eine Triade ausgeglichen, wenn entweder zwischen allen Knoten eine positive Beziehung besteht oder, wenn es genau ein positives Vorzeichen und zwei negative Vorzeichen gibt (Heider, 1946).
Tabelle 2: Balancierte und nicht balancierte 4-Zyklen
| \(\) 4-Zyklus \(\) | |
|---|---|
| \(\) \(+ + + +\) \(\) | \(\) balanciert \(\) |
| \(\) \(+ + - -\) | \(\) balanciert \(\) |
| \(\) \(- - - -\) | \(\) balanciert \(\) |
| \(\) \(+ + + -\) | \(\) nicht balanciert \(\) |
| \(\) \(+ - - -\) | \(\) nicht balanciert \(\) |
Bei Betrachtung der vollständig verknüpften 4-Zyklen in Tabelle 2 ergeben sich die fünf Vorzeichenkonstellationen, bei denen drei balanciert und zwei strukturell unausgeglichen sind.
Hierbei wird anhand der beiden Beispiele ersichtlich, dass ein Zyklus harmonisch ist, wenn die Anzahl der negativen Kanten in dem Zyklus gerade ist.
4.2. Berechnung der strukturellen Ausgeglichenheit in Netzwerken
Maß der strukturellen Ausgeglichenheit ohne Gewichtung der Zyklen (Formel 1):
Diese Formel gibt eine Auskunft über das Maß der strukturellen Ausgeglichenheit, indem die Anzahl der ausgeglichenen Zyklen durch die Anzahl aller Zyklen in einem untersuchten Netzwerk dividiert wird, ohne die Gewichtung der Kantenzahl der einzelnen Zyklen einzubeziehen.
Aus der Arbeit von Zheng, X., Zeng, D. und Wang, F.-Y. (Zheng et al., 2015) sowie der Empfehlung von Cartwright, D. und Harary, F. (Cartwright & Harary, 1956) folgt die Formel für die Berechnung der strukturellen Ausgeglichenheit ohne Gewichtung der Zyklen:
Formel 1:
\[B = \frac{ C_{ p_{ges} } }{ C_{ ges } } = \frac{ \sum{ }{}{ } C_{ p }}{ \sum{ }{}{ } C } = \frac{ \sum{ }{}{ } C_{ p }}{ \sum{ }{}{ } C_{p } + \sum{ }{}{ } C_{n } }\]Hierbei beschreibt \(C_{ p_{ges} }\) die Menge aller positiven Zyklen und \(C_{ ges }\) die Menge aller Zyklen. Daraus wird die Balance \(B\) des Netzwerkes bestimmt, indem die Anzahl aller positiven Zyklen \(C_{ p }\) durch die Anzahl aller Zyklen \(C\) in dem Netzwerk dividiert wird.
Die Gewichtung aller Knoten, ob balanciert oder nicht balanciert, beträgt dabei eins, sodass \(C_{ p } = C_{ n } = C = 1\) gilt. Zugleich gilt, dass sich die Summe aller Zyklen \(\sum{ }{}{ } C_{ }\) in dem untersuchten Netzwerk aus der Summe der positiven Zyklen \(\sum{ }{}{ } C_{ p }\) und der Summe der negativen Zyklen \(\sum{ }{}{ } C_{ n }\) zusammensetzt.
Berechnung der strukturellen Ausgeglichenheit mit Gewichtung der Zyklen (Formel 2):
Die Formel gibt eine Auskunft über das Maß der Balance, indem die Anzahl der ausgeglichenen Zyklen multipliziert mit der Kantenlänge durch die Anzahl aller Zyklen multipliziert mit der Kantenlänge dividiert wird. Dies erfolgt somit, indem die Gewichtung der Kantenzahl der einzelnen Zyklen berücksichtigt wird.
Die Formel für die Berechnung der strukturellen Ausgeglichenheit mit Gewichtung der Länge der Zyklen ist in Anlehnung an die Definition von Aref, S. und Wilson, M. C. (Aref & Wilson, 2018) definiert:
Formel 2:
\[B = \frac{ \sum{ }{}{ } k_{ p_i }\cdot C_{ p_i }}{ \sum{ }{}{ } k_{ i }\cdot C_{ i } } = \frac{ \sum{ }{}{ } k_{ p_i }\cdot C_{ p_i }}{ \sum{ }{}{ } k_{ p_i }\cdot C_{ p_i } + \sum{ }{}{ } k_{ n_i }\cdot C_{ n_i }}\]Mittels dieser Formel wird die Balance unter Berücksichtigung der Gewichtung der Kantenzahl der einzelnen Zyklen berechnet. Hierzu wird jeder balancierte und nicht balancierte Zyklus mit dessen Kantenzahl multipliziert. Nachdem diese mit ihrer Gewichtung multipliziert sind, wird die Summe über die Anzahl der balancierten Zyklen \(C_{ p_i }\) multipliziert mit der jeweiligen Kantenzahl \(k_{ p_i }\) gebildet. Zudem wird die Summe über die Anzahl der nicht strukturell ausgeglichenen Zyklen \(C_{ n_i }\) multipliziert mit der jeweiligen Kantenzahl \(k_{ n_i }\) berechnet. Darauf folgend wird im zweiten Schritt die Summe über die Anzahl aller Zyklen \(C_{ i }\) gebildet, indem die Summen der balancierten und nicht balancierten Zyklen multipliziert mit der jeweiligen Kantenzahl \(k_{ i }\) addiert werden. Im Anschluss wird die Summe der balancierten Zyklen mit Gewichtung durch die Summe aller Zyklen mit Gewichtung dividiert.
Analog zur vorherigen Formel gilt, dass sich \(C_{ i }\) aus den positiven Zyklen \(C_{ p_i }\) und negativen Zyklen \(C_{ n_i }\) zusammensetzt und stets gilt \(C_{ p_i } = C_{ n_i } = C_{ i } = 1\).
Berechnung der Triangel- und k-Balance (Formel 3):
Die Formel gibt eine Auskunft über das Maß der strukturellen Ausgeglichenheit, indem die Anzahl der ausgeglichenen k-Zyklen durch die Anzahl aller k-Zyklen in einem Netzwerk dividiert wird. Dies erfolgt, indem ausschließlich Zyklen mit einer festen Kantenzahl \(k\) für die Ermittlung der k-Balance berücksichtigt werden. Dabei ermöglicht es diese Formel, auf eine effiziente Art und Weise, eine Auskunft über die Balance eines Netzwerkes zu bekommen.
Im ersten Schritt wird hierbei die Triangel-Balance vorgestellt für Zyklen der Kantenlänge \(3\). Anschließend wird die k-Balance für Zyklen der Kantenlänge \(k\) betrachtet.
In Anlehnung an die Definition von Aref, S. und Wilson, M. C. (Aref & Wilson, 2018) ergibt sich die Formel für die Berechnung der 3-Balance:
Formel 3 (Triangel-Balance):
\[B_{ 3 } = \frac{ C_{ p_{ges_{3}} } }{ C_{ ges_{3} } } = \frac{ \sum{ }{}{ } C_{ p_{3} }}{ \sum{ }{}{ } C_{3} } = \frac{ \sum{ }{}{ } C_{ p_{3} }}{ \sum{ }{}{ } C_{p_{3} } + \sum{ }{}{ } C_{n_{3} } }\]Dabei setzt sich \(C_{ p_{ ges_{3} } }\) aus der Anzahl aller balancierten Zyklen der Kantenlänge \(3\) und \(C_{ ges_{3} }\) aus der Anzahl aller Zyklen der Kantenlänge \(3\) zusammen. Hierbei gilt, dass jeder Zyklus \(C_{3}\), \(C_{ p_{3} }\) und \(C_{ n_{3} }\) den Wert \(1\) hat.
Des Weiteren kann diese Formel für jede Kantenzahl \(k\) größer-gleich \(3\) angewendet werden, um eine Auskunft über die strukturelle Ausgeglichenheit in Abhängigkeit dieser Kantenzahl zu erhalten:
Formel 3 (k-Balance):
\[B_{ k } = \frac{ C_{ p_{ges_{k}} } }{ C_{ ges_{k} } } = \frac{ \sum{ }{}{ } C_{ p_{k} }}{ \sum{ }{}{ } C_{k} } = \frac{ \sum{ }{}{ } C_{ p_{k} }}{ \sum{ }{}{ } C_{p_{k} } + \sum{ }{}{ } C_{n_{k} } }\]Hierbei setzt sich \(C_{ p_{ ges_{k} } }\) aus der Anzahl aller balancierten Zyklen der Kantenlänge k und \(C_{ ges_{k} }\) aus der Anzahl aller Zyklen der Kantenlänge k zusammen. Es gilt ebenfalls, dass jeder Zyklus \(C_{k}\), \(C_{ p_{k} }\) und \(C_{ n_{k} }\) den Wert \(1\) hat.
Dieser Ansatz ersetzt keine ausführliche Analyse, kann aber ein Indiz für das Maß der strukturellen Ausgeglichenheit in einem vorzeichenbehafteten Netzwerk liefern.
5. Anwendung und Evaluierung der Ergebnisse
Erstens wird die Balance für drei Anwendungsbeispiele kleiner Netzwerke berechnet. Darauf folgend wird die strukturelle Ausgeglichenheit am Beispiel der Datensätze von Epinions, Slashdot und Wikipedia berechnet. Drittens wird eine Evaluierung und Diskussion der Ergebnisse durchgeführt. Abschließend erfolgt ein Fazit.
5.1. Berechnung der Balance am Beispiel kleiner Netzwerke
In diesem Kapitel werden die Formeln, die in Kapitel 4.2 definiert wurden, für die Berechnung der strukturellen Ausgeglichenheit auf drei kleine Netzwerke (mit 8 und 9 Knoten) angewendet.
Dazu werden die Netzwerke zuerst in Zyklen zerlegt, sodass die einzelnen Zyklen auf ihre strukturelle Ausgeglichenheit analysiert werden können. Auf Basis dieser Ergebnisse kann daraufhin die strukturelle Ausgeglichenheit des gesamten Netzwerkes berechnet werden. (Hierbei werden die Zyklen im Uhrzeigersinn, beginnend mit dem lexikographisch kleinsten Buchstaben, beschrieben.)
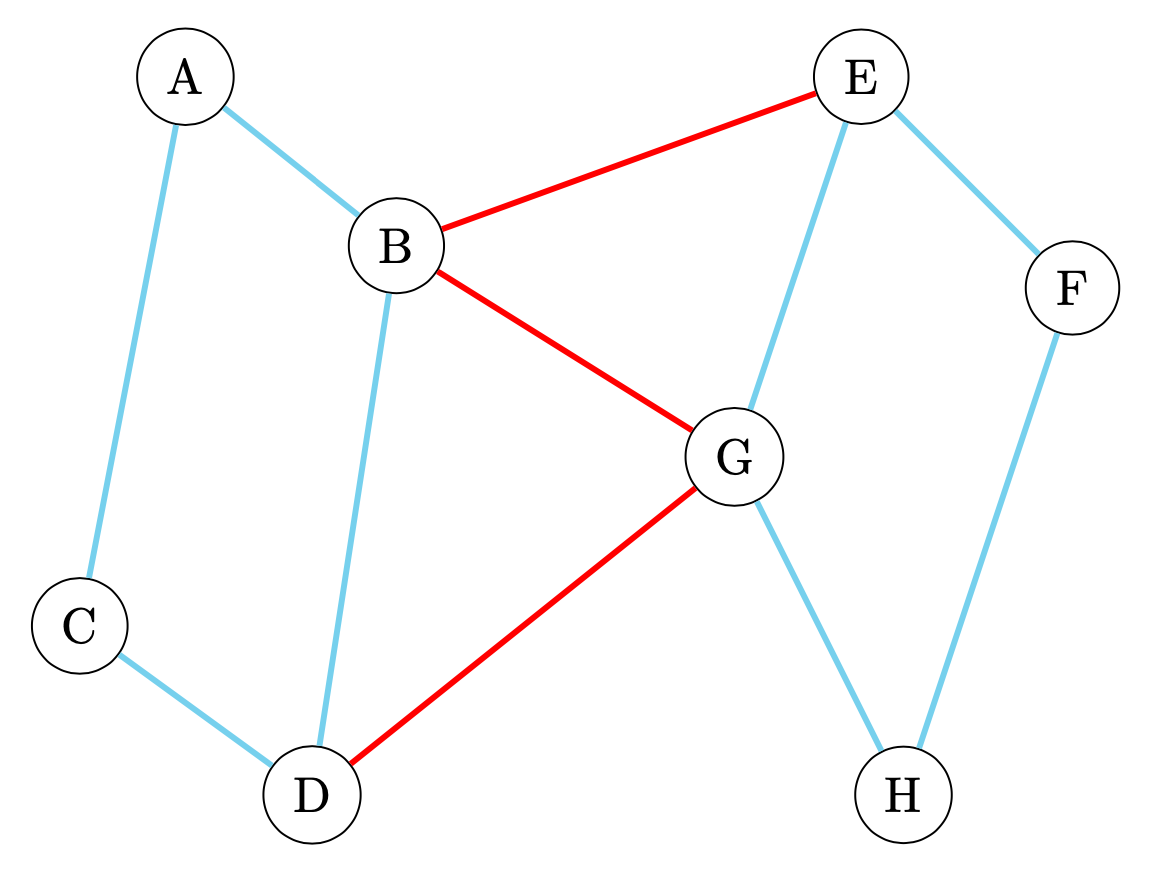 Abbildung 3: Strukturell ausgeglichenes vorzeichenbehaftetes Netzwerk (Galimberti et al., 2020)
Abbildung 3: Strukturell ausgeglichenes vorzeichenbehaftetes Netzwerk (Galimberti et al., 2020)
Der Graph aus Abbildung 1 besteht aus zwei Teilgraphen mit der Kantenzahl vier, in denen die Knoten ausschließlich durch positive (blaue) Kanten verbunden sind. Im Gegensatz zu den Teilgraphen, sind die Teilmengen lediglich durch negative (rote) Kanten verbunden. Nach der Zerlegung können die Formeln zur Berechnung der Balance angewendet werden, sodass folgt:
Formel 1 (ohne Gewichtung):
\[B = \frac{ C_{ p_{ges} } }{ C_{ ges } } = \frac{ 1 + 1 + 1 + 1 }{ 1 + 1 + 1 + 1 } = \frac{ 4 }{ 4 } = 1 = 100\%\]Formel 2 (mit Gewichtung):
\[B = \frac{ \sum{ }{}{ } k_{ p_i }\cdot C_{ p_i }}{ \sum{ }{}{ } k_{ i }\cdot C_{ i } } = \frac{ 3 + 3 + 4 + 4 }{ 3 + 3 + 4 + 4 } = \frac{6 + 8}{6 + 8} = \frac{ 14 }{ 14 } = 1 = 100\%\]Erläuterung zur Berechnung mit Formel 2:
In Formel 2 werden zuerst alle Zyklen der Länge 3 betrachtet. Aufgrund dessen, dass diese Zyklen alle positiv sind, wird die Anzahl der Triaden mit der Gewichtung \(3\) multipliziert. Dies ergibt \(3\cdot 1 + 3\cdot 1 = 3 + 3 = 2\cdot 3 = 6\). Darauf folgend wird die Anzahl der Zyklen der Länge \(4\) betrachtet und diese mit dem Faktor \(4\) multipliziert. Dies ergibt: \(4\cdot 1 + 4\cdot 1 = 4 + 4 = 2\cdot 4 = 8\). Aufgrund dessen, dass keine größeren Zyklen existieren, werden die Ergebnisse addiert, sodass folgt: \(3 + 3 + 4 + 4 = 6 + 8 = 14\). Somit liefert die Formel 2 als Ergebnis den Wert \(1\) für das Maß der Balance.
Gemäß dieser Berechnungen liefern Formel 1 und 2 den Wert \(1\) als Ergebnis für die Balance, weil das Netzwerk lediglich aus positiven Zyklen besteht. Dementsprechend gilt das Netzwerk per Definition als strukturell ausgeglichen, weil alle Zyklen in diesem Graphen balanciert sind (Cartwright & Harary, 1956).
Formel 3 (3-Balance):
\[B_{ 3 } = \frac{ C_{ p_{ges_{3}} } }{ C_{ ges_{3} } } = \frac{ 6 }{ 6 } = 1 = 100\%\]Formel 3 (4-Balance):
\[B_{ 4 } = \frac{ C_{ p_{ges_{4}} } }{ C_{ ges_{4} } } = \frac{ 8 }{ 8 } = 1 = 100\%\]Die Formel 3 liefert ebenfalls als Ergebnis den Wert \(1\) für die Balance bei der 3- und 4-Balance, weil alle Zyklen im Netzwerk positiv sind.
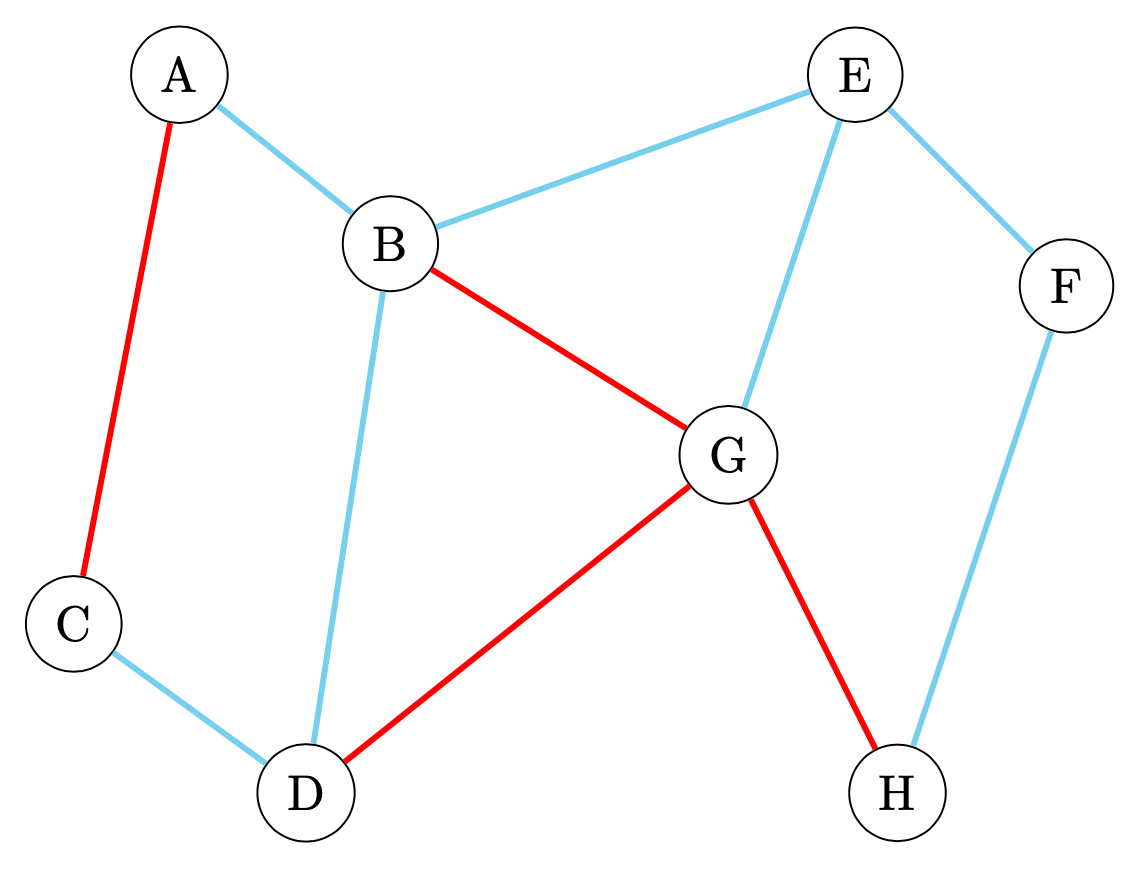 Abbildung 2: Strukturell unausgeglichenes vorzeichenbehaftetes Netzwerk (Galimberti et al., 2020)
Abbildung 2: Strukturell unausgeglichenes vorzeichenbehaftetes Netzwerk (Galimberti et al., 2020)
Der Graph aus Abbildung 2 besteht ebenfalls aus zwei Teilgraphen mit der Kantenzahl vier. Hierbei enthalten die zwei Zyklen der Länge vier genau eine negative Kante, sodass diese nicht balanciert sind. Ebenfalls bilden die drei Kanten, die beide Teilgraphen verbinden, zwei Triaden, wovon eine Triade ausgeglichen und die andere nicht strukturell ausgeglichen ist. Daraus folgt, dass die Zyklen ABDC, EFHG und BEG nicht balanciert sind und ausschließlich BGD strukturell ausgeglichen ist. Nach der Zerlegung können die Formeln zur Berechnung der Balance angewendet werden, sodass folgt:
Formel 1 (ohne Gewichtung):
\[B = \frac{ C_{ p_{ges} } }{ C_{ ges } } = \frac{ 1 }{ 4 } = 0,25 = 25\%\]Formel 2 (mit Gewichtung):
\[B = \frac{ \sum{ }{}{ } k_{ p_i }\cdot C_{ p_i }}{ \sum{ }{}{ } k_{ i }\cdot C_{ i } } = \frac{ 3 }{ 14 } = 0,2142 = 21,42\%\]Formel 3 (3-Balance):
\[B_{ 3 } = \frac{ C_{ p_{ges_{3}} } }{ C_{ ges_{3} } } = \frac{ 3 }{ 3+3 }= 0,5 = 50\%\]Formel 3 (4-Balance):
\[B_{ 4 } = \frac{ C_{ p_{ges_{4}} } }{ C_{ ges_{4} } } = \frac{ 0 }{ 4+4 } = 0 = 0\%\]Dabei liefert Formel 1 den Wert \(0,25\) \((25\%)\) und Formel 2 den Wert \(0,2142\) \((21,42\%)\) als Ergebnis für die Balance. Somit kann der Graph auf Basis dieser ermittelten Ergebnisse als strukturell unausgeglichen bezeichnet werden (Cartwright & Harary, 1956).
Gleichzeitig liefert hierbei Formel 3 eine genauere Auskunft über die Balance in Abhängigkeit der Kantenzahl, wobei die Triaden-Balance einen Wert der strukturellen Ausgeglichenheit von \(0,5\) \((50\%)\) und die 4-Balance einen Wert der Balance von \(0\) \((0\%)\) aufweist.
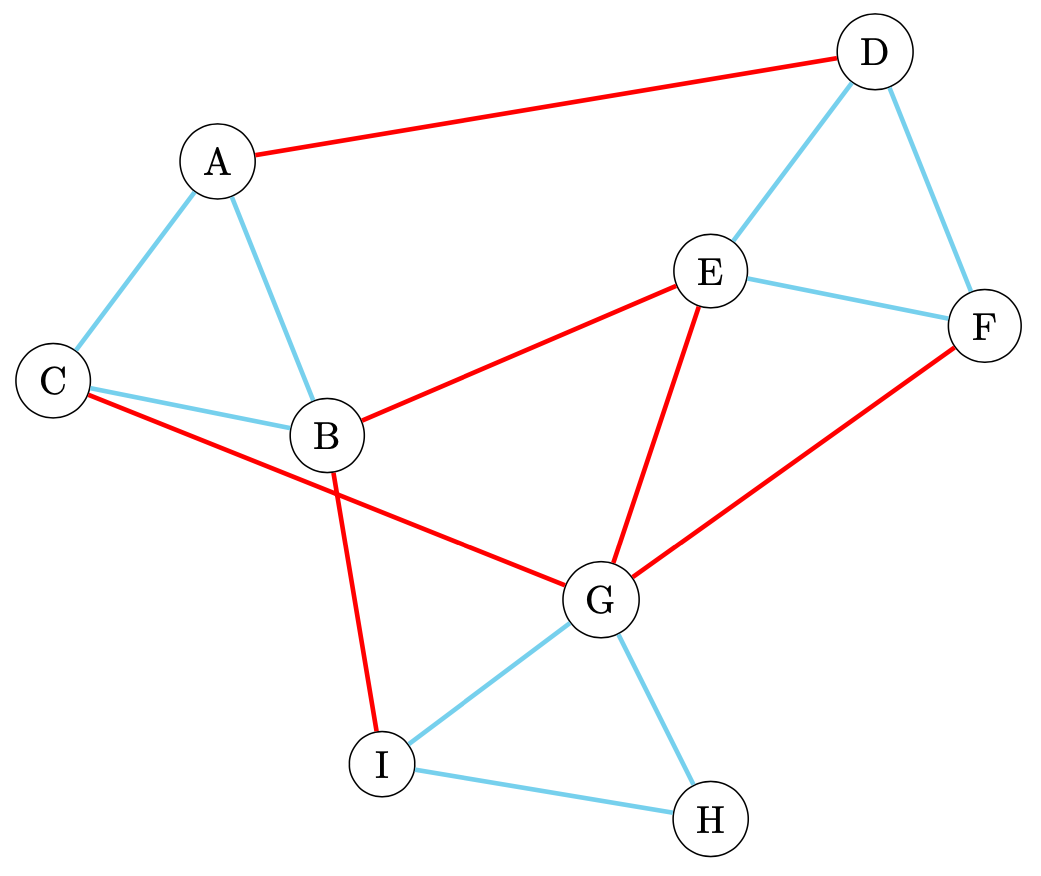 Abbildung 3: Vorzeichenbehaftetes Netzwerk (Anchuri & Ismail, 2012)
Abbildung 3: Vorzeichenbehaftetes Netzwerk (Anchuri & Ismail, 2012)
Aus Abbildung 3 geht hervor, dass das Netzwerk aus vier Triaden mit ABC, DFE, GHI und EFG sowie aus drei 4-Zyklen mit ADEB, BEGC und BEGI besteht. Nach der Zerlegung können die Formeln zur Berechnung der Balance angewendet werden, sodass folgt:
Formel 1 (ohne Gewichtung):
\[B = \frac{ C_{ p_{ges} } }{ C_{ ges } } = \frac{ 1+1+1+1+1 }{ 7 } = \frac{ 5 }{ 7 } = 0,7143 = 71,43\%\]Formel 2 (mit Gewichtung):
\[B = \frac{ \sum{ }{}{ } k_{ p_i }\cdot C_{ p_i }}{ \sum{ }{}{ } k_{ i }\cdot C_{ i } } = \frac{ 3+3+3+3+4 }{ 3+3+3+3+4+4+4 } = \frac{ 16 }{ 24 } = 0,6667 = 66,67\%\]Formel 3 (3-Balance):
\[B_{ 3 } = \frac{ C_{ p_{ges_{3}} } }{ C_{ ges_{3} } } = \frac{4\cdot 3 }{ 4\cdot 3 } = 1 = 100\%\]Formel 3 (4-Balance):
\[B_{ 4 } = \frac{ C_{ p_{ges_{4}} } }{ C_{ ges_{4} } } = \frac{ 4 }{ 4+4+4 } = 0,3333 = 33,33\%\]Hierbei ist eine Differenz von \(0,0476\) \((4,76\%)\) zwischen den Ergebnissen aus Formel 1 und Formel 2 ersichtlich. Durch eine folgende Analyse mittels Formel 3 wird daraufhin erkennbar, dass sich das Maß der Balance der Triaden und der 4-Zyklen um eine Differenz von \(0,6667\) \((66,67\%)\) unterscheidet.
5.2. Berechnung der strukturellen Ausgeglichenheit am Beispiel der Datensätze von Epinions, Slashdot und Wikipedia
Im Folgenden werden die Datensätzen von Epinions, Slashdot Zoo und Wikipedia-Elect untersucht, die eine Auskunft über die Anwendbarkeit der vorgestellten Formeln auf reale, große Datensätze geben sollen. Diese Datensätze sind auf der Website der Stanford Large Network Dataset Collection unter der Rubrik der vorzeichenbehafteten Netzwerke einsehbar und abrufbar (Stanford Large Network Dataset Collection, 27.06.2021).
Bei Epinions handelt es sich um ein soziales Netzwerk für Produktrezessionen für Privatkunden, das von dem Preisvergleichs-Portal Shopping.com übernommen wurde. Slashdot ist eine primär Technologie-orientierte News-Website für spezielle Communities, wobei Slashdot Zoo ein Bestandteil der Dienstleistung ist und es Nutzern ermöglicht, sich gegenseitig als Freund oder Feind einzuschätzen. Bei den Wikipedia Adminship Election Daten handelt es sich um abgegebene Stimmen der Wikipedia Community, um per Wahl zu bestimmen, ob Nutzer der Plattform in den administrativen Status befördert werden oder nicht. Dabei enthalten diese Daten Informationen, ob ein Mitglieder der Wikipedia Community für oder gegen die Beförderung eines Kandidaten gestimmt hat (Stanford Large Network Dataset Collection, 27.06.2021).
5.2.1. Anwendung 1
Tabelle 3: Anzahl an balancierten und nicht strukturell ausgeglichenen nicht-gerichteten Triaden, wobei die ersten zwei Zeilen balanciert sowie die letzten zwei Zeilen nicht balanciert sind
| \(\) Triade \(\) | \(\) Epinions \(\) | \(\) Slashdot \(\) |
|---|---|---|
| \(\) \(+ + +\) \(\) | \(\) \(4.003.085\) \(\) | \(\) \(414.956\) \(\) |
| \(\) \(+ - -\) | \(\) \(\) \(\) \(\) \(396.548\) \(\) | \(\) \(\) \(\) \(76.859\) \(\) |
| \(\) \(+ + -\) | \(\) \(\) \(\) \(\) \(451.711\) \(\) | \(\) \(\) \(\) \(66.679\) \(\) |
| \(\) \(- - -\) | \(\) \(\) \(\) \(\) \(\) \(\) \(58.732\) \(\) | \(\) \(\) \(\) \(12.075\) \(\) |
Anhand der Anzahl der balancierten und nicht balancierten 3-Zyklen aus Tabelle 3 wird die strukturelle Ausgeglichenheit der Triaden basierend auf Formel 3 berechnet:
Anwendung der Formel 3:
\[B_{ 3 } = \frac{ C_{ p_{ges_{3}} } }{ C_{ ges_{3} } }\]Balance \(B_{ 3 }\) für Epinions:
\[B_{ 3 } = \frac{ 4.003.085 + 396.548 }{ 4.003.085 + 396.548 + 451.711 + 58.732 } = 0,8960 = 89,60\%\]Balance \(B_{ 3 }\) für Slashdot:
\[B_{ 3 } = \frac{ 414.956 + 76.859 }{ 414.956 + 76.859 + 66.679 + 12.075 } = 0,8620 = 86,20\%\]Hierbei wird ersichtlich, dass die 3-Balance für Epinions einen Wert von \(0,8960\) \((89,60\%)\) und für Slashdot einen Wert von \(0,8620\) \((86,20\%)\) aufweist.
5.2.2. Anwendung 2
Tabelle 4: Statistik der balancierten und nicht balancierten 3- und 4-Zyklen. Die ersten sechs Zyklen sind balanciert und die folgenden vier Zyklen sind nicht strukturell ausgeglichen. Des Weiteren stellen die letzten zwei Zeilen die Summe aus den zuvor bestimmten Ergebnissen der gelisteten balancierten 3- und 4-Zyklen dar und geben eine Auskunft über die 3- und 4-Balance in den untersuchten Netzwerken
| \(\) Zyklus \(\) | \(\) Epinions \(\) | \(\) Slashdot \(\) | \(\) Wikipedia \(\) |
|---|---|---|---|
| \(\) \(+ + +\) | \(\) \(\) \(0,8259\) \(\) | \(\) \(0,7301\) \(\) | \(\) \(0,6996\) \(\) \(\) \(\) |
| \(\) \(+ - -\) | \(\) \(\) \(0,0791\) \(\) | \(\) \(0,1364\) \(\) | \(\) \(0,0840\) \(\) \(\) \(\) |
| \(\) \(+ + + +\) | \(\) \(\) \(0,7538\) \(\) | \(\) \(0,6723\) \(\) | \(\) \(0,6080\) \(\) \(\) \(\) |
| \(\) \(+ + - -\) | \(\) \(\) \(0,0911\) \(\) | \(\) \(0,1127\) \(\) | \(\) \(0,1007\) \(\) \(\) \(\) |
| \(\) \(+ - + -\) | \(\) \(\) \(0,0065\) \(\) | \(\) \(0,0138\) \(\) | \(\) \(0,0139\) \(\) \(\) \(\) |
| \(\) \(- - - -\) | \(\) \(\) \(0,0103\) \(\) | \(\) \(0,0263\) \(\) | \(\) \(0,0054\) \(\) \(\) \(\) |
| \(\) \(+ + -\) | \(\) \(\) \(0,0834\) \(\) | \(\) \(0,1125\) \(\) | \(\) \(0,2052\) \(\) \(\) \(\) |
| \(\) \(- - -\) | \(\) \(\) \(0,0117\) \(\) | \(\) \(0,0211\) \(\) | \(\) \(0,0013\) \(\) \(\) \(\) |
| \(\) \(+ + + -\) | \(\) \(\) \(0,1174\) \(\) | \(\) \(0,1413\) \(\) | \(\) \(0,2473\) \(\) \(\) \(\) |
| \(\) \(+ - - -\) | \(\) \(\) \(0,0208\) \(\) | \(\) \(0,0337\) \(\) | \(\) \(0,0247\) \(\) \(\) \(\) |
| \(\) Balancierte \(3\)-Zyklen \(\) | \(\) \(\) \(0,9050\) \(\) | \(\) \(0,8665\) \(\) | \(\) \(0,7835\) \(\) \(\) \(\) |
| \(\) Balancierte \(4\)-Zyklen \(\) | \(\) \(\) \(0,8617\) \(\) | \(\) \(0,8250\) \(\) | \(\) \(0,7280\) \(\) \(\) \(\) |
Die Ergebnisse der balancierten 3- und 4-Zyklen aus den letzten beiden Zeilen der Tabelle sind analog zu Formel 3 aus Kapitel 4.2. Zudem indizieren diese letzten beiden Zeilen aus Tabelle 4, dass die 3-Zyklen im Vergleich zu den 4-Zyklen mit höherer Wahrscheinlichkeit balanciert sind (Chiang et al., 2013).
Anwendung der Formeln 1 und 2:
Aufgrund dessen, dass die exakte Anzahl der 3- und 4-Zyklen nicht vorliegt, werden die Formeln 1 und 2 für das Maß der strukturellen Ausgeglichenheit näherungsweise auf Basis der Ergebnisse der 3- und 4-Balance aus Tabelle 4 mithilfe einer adaptierten Variante der Formeln berechnet. Diese wird bestimmt, indem der Anteil der balancierten 3-Zyklen mit dem Anteil der balancierten 4-Zyklen addiert wird und nachfolgend durch \(2\) dividiert wird.
Formel 1:
\[B = \frac{ C_{ p_{ges} } }{ C_{ ges } }\]Näherungsweise für die Balance ohne Gewichtung wird gemäß adaptierter Variante der Formel berechnet:
Epinions:
\[B = \frac{ 0,9050 + 0,8617 }{ 1+1 } = 0,8834 = 88,34\%\]Slashdot:
\[B = \frac{ 0,8665 + 0,8250 }{ 1+1 } = 0,8458 = 84,58\%\]Wikipedia:
\[B = \frac{ 0,7835 + 0,7280 }{ 1+1 } = 0,7558 = 75,58\%\]Formel 2:
\[B = \frac{ \sum{ }{}{ } k_{ p_i }\cdot C_{ p_i }}{ \sum{ }{}{ } k_{ i }\cdot C_{ i } }\]Näherungsweise für die Balance mit Gewichtung der Kantenzahl wird gemäß adaptierter Variante der Formel berechnet:
Epinions:
\[B = \frac{ 0,9050\cdot 3 + 0,8617\cdot 4 }{ 1\cdot 3 + 1\cdot 4 } = 0,8803 = 88,03\%\]Slashdot:
\[B = \frac{ 0,8665\cdot 3 + 0,8250\cdot 4 }{ 1\cdot 3 + 1\cdot 4 } = 0,8428 = 84,28\%\]Wikipedia:
\[B = \frac{ 0,7835\cdot 3 + 0,7280\cdot 4 }{ 1\cdot 3 + 1\cdot 4 } = 0,7519 = 75,19\%\]Es gilt hierbei zu beachten, dass mittels der adaptierten Varianten der Formeln eine Vereinfachung vorgenommen wurde, sodass abweichende Ergebnisse möglich und zu erwarten sind. Dies ist der Fall, weil die Formeln bei der adaptierten Varianten auf die bereits vorliegende 3- und 4-Balance angewandt wurden, anstatt auf die tatsächliche Anzahl der Zyklen in Abhängigkeit ihrer Kantenzahl.
5.3. Evaluierung und Diskussion der Ergebnisse
Bei der Betrachtung der Ergebnisse in Kapitel 5.1 wird sichtbar, dass mithilfe der Analyse durch die vorgestellten Formeln eine Auskunft über das Maß der strukturellen Ausgeglichenheit in vorzeichenbehafteten Netzwerken erzielt werden kann, indem alle drei Formeln auf ein Netzwerk angewendet werden. Wobei Formel 3 mit unterschiedlichen Werten für die Kantenzahl \(k\) angewendet werden sollte, weil insbesondere durch die Analyse von Abbildung 3 mittels Formel 3 ersichtlich wurde, dass sich das Maß der Balance der Triaden und der 4-Zyklen verhältnismäßig stark unterscheiden kann. Dementsprechend ist es stets hilfreich und empfehlenswert, alle drei der vorgestellten Formeln für die Analyse der strukturellen Ausgeglichenheit zu verwenden und ebenfalls die Differenz zwischen den Ergebnissen der Formeln 1 und 2 sowie zwischen den Ergebnissen der Formel 3 in Abhängigkeit von unterschiedlichen Kantenzahlen \(k\) zu untersuchen.
Des Weiteren wird bei der Analyse der großen Netzwerke in Kapitel 5.2 sichtbar, dass sich die Formeln eignen, um eine Auskunft über die Balance in großen Netzwerken zu erhalten. Beispielsweise wird mithilfe der Berechnung der strukturellen Ausgeglichenheit durch die Formeln 1 und 2 ersichtlich, nachdem die Differenz zwischen den Ergebnissen der beiden Formeln gebildet wird, dass der Wert der strukturellen Ausgeglichenheit ohne Gewichtung aus Formel 1 um \(0,31\%\) bei Epinions, um \(0,30\%\) bei Slashdot und um \(0,39\%\) bei Wikipedia größer ist im Vergleich zu dem Wert der Balance mit Gewichtung, der mit Formel 2 berechnet wurde. Darüber hinaus kann zugleich mittels Formel 3 in Abhängigkeit von unterschiedlichen Kantenzahlen ein großes Netzwerk weiterführend analysiert werden sowie können auf Basis dieser Ergebnisse zusätzliche Informationen über die strukturelle Ausgeglichenheit des Netzwerkes gewonnen werden.
Zudem konnte bei dem Vergleich der 3- und 4-Balance sowie per Berechnung des Erwartungswertes im Anhang festgestellt werden, dass mit zunehmender Kantenzahl in den k-Zyklen das Maß der strukturellen Ausgeglichenheit abnimmt. Dementsprechend liefert die Analyse der 3-Zyklen in den meisten Fällen einen guten Richtwert für die Balance und es ist zu erwarten, dass der Wert für das Maß der strukturellen Ausgeglichenheit des gesamten Netzwerkes unterhalb des Wertes der 3-Balance liegt.
5.4. Fazit
Ein Netzwerk gilt als strukturell ausgeglichen anhand des vorgestellten Ansatzes, wenn alle Zyklen balanciert sind (Cartwright & Harary, 1956). Aus den Beispielen in Kapitel 5.1 geht hervor, dass dies in kleinen Netzwerken möglich ist und dort ein Maß für die Balance von \(1\) erreicht werden kann.
Allerdings geht aus den Datensätzen in Kapitel 5.2 hervor, dass es unmöglich ist, dies durch die Analyse der Zyklen in großen Netzwerken zu erreichen. Dementsprechend folgt die Frage, ab welchem Maß mittels dieses Ansatzes von einer guten strukturellen Ausgeglichenheit gesprochen werden kann. Grundsätzlich gilt hierbei, dass individuell unterschieden werden muss, je nach der Art und dem Zweck des Netzwerkes. Diesbezüglich ist es sinnvoll, das Ergebnis für das Maß der Balance für das untersuchte große Netzwerk mit anderen ähnlichen Netzwerken zu vergleichen sowie die Einschätzung und Bewertung für das Maß der Balance davon abhängig zu machen. Ist das untersuchte Netzwerk darüber hinaus dynamisch, so empfiehlt es sich ebenfalls, in regelmäßigen Abständen die strukturelle Ausgeglichenheit zu prüfen sowie die Entwicklung von dem Maß der Balance zu verfolgen. Denn aus diesen Informationen können weitere Rückschlüsse über die strukturelle Ausgeglichenheit in dem vorzeichenbehafteten Netzwerk gezogen werden.
Liegt das Maß der strukturellen Ausgeglichenheit nahe \(1\), so kann tendenziell von einem hohen Maß der Balance in dem untersuchten Netzwerk gesprochen werden.
6. Zusammenfassung und Ausblick
Das Ziel der Arbeit bestand darin, Erkenntnisse für die Berechnung der strukturellen Ausgeglichenheit anhand der Analyse der Zyklen in vorzeichenbehafteten Netzwerken zu gewinnen, sodass diese für eine effiziente Bewertung gleichartiger Netzwerke genutzt werden können. Hierzu wurden geeignete Formeln zur Berechnung der Balance vorgestellt sowie per Erwartungswert und Beobachtung ermittelt, dass die Analyse der 3-Zyklen und 4-Zyklen einen ersten Richtwert über das Maß der strukturellen Ausgeglichenheit in einem großen vorzeichenbehafteten Netzwerk liefern kann. Gleichzeitig konnte bestätigt werden, dass die Berechnung der strukturellen Ausgeglichenheit auf Basis der Zyklen in vorzeichenbehafteten Netzwerken eine gute Möglichkeit darstellt, eine verlässliche und hinreichende Auskunft über das Maß der Balance zu erhalten.
Gleichzeitig wurden Vereinfachungen innerhalb dieser Arbeit bei der Auswertung der realen, großen Datensätze vorgenommen, indem die Analyse auf die 3- und 4-Zyklen beschränkt wurde sowie die Formeln 1 und 2 auf Basis von Näherungswerten berechnet wurden. Es bietet sich dementsprechend an, eine weiterführende, umfangreichere Arbeit diesen Ergebnissen anzuschließen, bei der die Datensätze der Stanford Large Network Dataset Collection zu vorzeichenbehafteten Netzwerken (Stanford Large Network Dataset Collection, 27.06.2021) mit geeigneten Algorithmen exakter untersucht werden, sodass die genau Anzahl aller k-Zyklen für \(k\) größer-gleich \(3\) bis beispielsweise \(k\) gleich \(30\) ermittelt werden. Dabei könnte mittels einer solchen Auswertung die exakte Menge der balancierten und nicht balancierten Zyklen der jeweiligen Kantenzahl bestimmt werden, sodass mittels dieser Daten eine Anwendung der vorgestellten Formeln auf die großen, realen Netzwerke präziser umsetzbar wäre.
Anhang
Erwartungswert-Berechnung für die Balance von k-Zyklen
Die folgenden Erwartungswerte werden auf Basis des Anteils an positiven und negativen Kanten in dem gesamten Netzwerk berechnet. Mithilfe dieser Erwartungswerte soll eine Auskunft über die Tendenz und Entwicklung der zu erwartenden strukturellen Ausgeglichenheit in Abhängigkeit der Kantenzahl gegeben werden, die bei der Analyse großer Netzwerke unterstützend dienen sollen.
Dabei werden die Formeln für die k-Zyklen mit ungerader und gerader Anzahl an Kanten allgemeingültig aufgestellt und nachfolgend auf den Datensatz von Bitcoin-OTC angewendet, um die Erwartungswerte für die k-Zyklen mit der Kantenzahl \(k = 3\) bis \(k = 10\) zu berechnen. Der Bitcoin-OTC Datensatz wird hierbei gewählt, weil in diesem vorzeichenbehafteten Netzwerk die Quote an positiven Kanten verhältnismäßig hoch ist mit \(89\%\) und der Datensatz mit \(5.881\) Knoten und \(35.592\) Kanten den Anforderungen an ein großes Netzwerk entspricht (Stanford Large Network Dataset Collection, 27.06.2021). Der Anteil an negativen Kanten beträgt hierbei \(11\%\).
Der Datensatz beschreibt eine Plattform namens Bitcoin-OTC auf der Personen mit Bitcoin handeln. Aufgrund dessen, dass Bitcoin-Nutzer anonym sind, werden die Benutzer von anderen Mitgliedern bewertet, um Transaktionen mit riskanten oder betrügerischen Nutzern zu verhindern. Dabei bewerten die Mitglieder von Bitcoin-OTC andere Mitglieder auf einer Skala von -10 bis +10 in Schritten von 1, wobei -10 der Höchstwert für Misstrauen und +10 der Höchstwert für Vertrauen darstellt. (Stanford Large Network Dataset Collection, 27.06.2021)
Maß der strukturellen Ausgeglichenheit in Abhängigkeit der Kantenzahl:
Es gilt für eine ungerade Anzahl an Kanten:
\[E(C_{ p_k }) = E(p)^{k} + \sum_{i=1}^{\frac{k-1}{2}} {k\choose k-2i} \cdot E(p)^{k-2i} \cdot E(n)^{2i}\]Es gilt für eine gerade Anzahl an Kanten:
\[E(C_{ p_k}) = E(p)^{k} + \sum_{i=1}^{\frac{k}{2}} {k\choose k-2i} \cdot E(p)^{k-2i} \cdot E(n)^{2i}\]Hierbei beschreiben \(E(p)\) den Erwartungswert für eine positive Kante sowie \(E(n)\) den Erwartungswert für eine negative Kante in dem untersuchten Netzwerk, wobei der Erwartungswert aus dem Anteil der positiven und negativen Kanten bestimmt wird. Darauf basierend wird der Erwartungswert für einen ausgeglichenen Zyklus \(E(C_{ p_k })\) in Abhängigkeit der Kantenlänge \(k\) des Zyklus bestimmt.
Maß der strukturellen Unausgeglichenheit in Abhängigkeit der Kantenzahl:
Es gilt für eine ungerade sowie gerade Anzahl an Kanten:
\[E(C_{ n_k }) = 1 - E(C_{ p_k })\]Dabei wird der Erwartungswert für einen unausgeglichenen Zyklus \(E(C_{ n_k })\) in Abhängigkeit der Kantenlänge \(k\) des Zyklus bestimmt.
Erwartungswert der Balance für k-Zyklen am Beispiel von Bitcoin-OTC:
Tabelle 5: Erwartungswert der Balance für k-Zyklen am Beispiel von Bitcoin-OTC für die Kantenzahl \(k = 3\) bis \(k = 10\) (Ergebnisse sind auf 2 Nachkommastellen gerundet)
| \(\) \(k\) \(\) | \(\) \(E(C_{ p_k })\) \(\) | \(\) \(E(C_{ n_k })\) \(\) |
|---|---|---|
| \(\) \(3\) | \(\) \(73,73\%\) \(\) | \(\) \(26,27\%\) \(\) |
| \(\) \(4\) | \(\) \(68,51\%\) \(\) | \(\) \(31,49\%\) \(\) |
| \(\) \(5\) | \(\) \(64,44\%\) \(\) | \(\) \(35,56\%\) \(\) |
| \(\) \(6\) | \(\) \(61,26\%\) \(\) | \(\) \(38,74\%\) \(\) |
| \(\) \(7\) | \(\) \(58,78\%\) \(\) | \(\) \(41,22\%\) \(\) |
| \(\) \(8\) | \(\) \(56,85\%\) \(\) | \(\) \(43,15\%\) \(\) |
| \(\) \(9\) | \(\) \(55,34\%\) \(\) | \(\) \(44,66\%\) \(\) |
| \(\) \(10\) \(\) | \(\) \(54,17\%\) \(\) | \(\) \(45,83\%\) \(\) |
Somit ist erkennbar, dass der Erwartungswert für einen strukturell ausgeglichenen Zyklus mit zunehmender Zyklen-Länge abnimmt und der Erwartungswert für einen unausgeglichenen Zyklus mit zunehmender Zyklen-Länge zunimmt.
Referenzen
- Zheng, X., Zeng, D., & Wang, F.-Y. (2015). Social balance in signed networks. Information Systems Frontiers, 17(5), 1077–1095. https://doi.org/10.1007/s10796-014-9483-8
- Aref, S., & Wilson, M. C. (2018). Measuring partial balance in signed networks. Journal of Complex Networks, 6(4), 566–595. https://doi.org/10.1093/comnet/cnx044
- Kirkley, A., Cantwell, G. T., & Newman, M. E. J. (2019). Balance in signed networks. Physical Review. E, 99(1-1), 012320. https://doi.org/10.1103/PhysRevE.99.012320
- Aref, S., & Wilson, M. C. (2019). Balance and frustration in signed networks. Journal of Complex Networks, 7(2), 163–189. https://doi.org/10.1093/comnet/cny015
- Newman, M. (2018). (Vol. 1). Oxford University Press. https://doi.org/10.1093/oso/9780198805090.001.0001
- Cartwright, D., & Harary, F. (1956). Structural balance: a generalization of Heider’s theory. Psychological Review, 63(5), 277–293. https://doi.org/10.1037/h0046049
- Tang, J., Chang, Y., Aggarwal, C. C., & Liu, huan. (2015). A Survey of Signed Network Mining in Social Media. CoRR, abs/1511.07569. http://arxiv.org/abs/1511.07569
- Chiang, H., Natarajan, T., & Dhillon. (2013). Prediction and Clustering in Signed Networks: A Local to Global Perspective. In Journal of Machine Learning Research.
- Doreian, P., & Mrvar, A. (1996). A Partitioning Approach to Structural Balance. Social Networks, 18(2), 149–168. http://www.sciencedirect.com/science/article/pii/0378873395002596
- Heider, F. (1946). Attitudes and cognitive organization. The Journal of Psychology, 21, 107–112. https://doi.org/10.1080/00223980.1946.9917275
- Galimberti, E., Madeddu, C., Bonchi, F., & Ruffo, G. (2020). Visualizing Structural Balance in Signed Networks. In H. Cherifi, S. Gaito, J. F. Mendes, E. Moro, & L. M. Rocha (Eds.), Complex Networks and Their Applications VIII (Vol. 882, pp. 53–65). Springer International Publishing. https://doi.org/10.1007/978-3-030-36683-4\textunderscore 5
- Anchuri, P., & Ismail, M. M. (2012). Communities and Balance in Signed Networks: A Spectral Approach. Proceedings of the 2012 IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining (ASONAM 2012), 235–242. https://doi.org/10.1109/ASONAM.2012.48
- Stanford Large Network Dataset Collection. (27.06.2021). https://snap.stanford.edu/data/#signnets