Neue OCDA für Multilayer-Netzwerke
| Phuong Nguyen |
|---|
| RWTH Aachen University |
| phuong.nguyen1@rwth-aachen.de |
| Julian Albers |
|---|
| RWTH Aachen University |
| julian.albers@rwth-aachen.de |
| Patrick Nachtigall |
|---|
| RWTH Aachen University |
| patrick.nachtigall@rwth-aachen.de |
Abstract
Klassische Overlapping Community Detection Algorithmen versuchen Communities zu entdecken und zu analysieren, wozu sie Graphen verwenden, um beispielsweise Beziehungen und Zusammenhänge in sozialen Strukturen darzustellen. Anders als diese Modellierung sind die Sachverhalte die wir mit diesen Graphen modelieren wollen aber oft nicht eindimensional. Beispielsweise nehmen wir eine Person oft in mehreren verschiedenen Rollen und Kontexten wahr.
Um sich dieser komplexeren und vielschichtigen Struktur besser anzunähern, können Multilayer Graphen verwendet werden. Da sich die bisherigen Analysealgorithmen von Graphen allerdings nicht ohne weiteres auf die Multilayer Graphen übertragen lassen, müssen neue Algorithmen entwickelt werden.
Die Aufgabe dieser Algorithmen besteht darin Knoten in einem Netzwerk zu finden, die stärker vernetzt sind als andere, diese Gruppen von Knoten werden als Communities bezeichnet.
Um einen Überblick über verschiedene Algorithmen und Ansätze zu geben um sich diesem Problem zu nähern werden wir im Folgenden drei verschiedene dieser Algorithmen, beziehungsweise Ansätze vorstellen.
___
Inhaltsverzeichnis
1. Einleitung
Durch OCD Algorithmen lassen sich Communities in Netzwerken identifizieren. Multilayernetzwerke sind in der Art besonders, dass sie, anders als einschichtige Netzwerke, in der Lage sind Gemeinschaften aus verschiedenen Kontexten, wie unterschiedlichen Social-Media-Plattformen, miteinander in Beziehung zu setzen. Deshalb ist es von Interesse Algorithmen zu finden, die auf Multilayernetzwerken operieren können (“Multilayer Networks,” 2014).
Bei der Anwendung auf Multilayernetzwerke können, wie bei einschichtigen Netzwerken, viele Algorithmen nur ungewichtete, Netzwerke betrachten. Gewichtete Graphen stellen meist die Realität genauer dar, weshalb wir zwei Algorithmen betrachten, die gewichtete Graphen behandeln können, und einen anderen Algorithmus betrachten, der adjazenzmatrixbasiert ist.
Der erste Algorithmus basiert auf Wahrscheinlichkeiten, mit die Knoten in einer Gemeinschaft bleiben. Diese Wahrscheinlichkeit wird durch Random Walks festgestellt. Die Grundlage des zweiten Algorithmus hingegen ist das Auffüllen eines Metagraphen nach Umherschieben der Knoten zur Gemeinschaftsermittlung. Dieser Ansatz ist Louvain-basiert. Schließlich wird noch ein evolutionärer Algorithmus vorgestellt, deren Grundlage die genetische Repräsentation von Elementen und die sogenannte „Fitness Funktion“ ist, die die Summe von Modularitäten berechnet.
Im Folgenden wird gezeigt, wie all diese Algorithmen auf Multilayernetzwerken laufen können.
2. Verwandte Arbeiten
In unserer Arbeit werden drei neue Overlapping Community Detection Algorithmen für Multilayer-Netzwerke vorstellen.
Das erste Kapitel befasst sich mit Random Walks, dabei beziehen wir uns vorallem auf (JEUB et al., 2017). Es werden zwei verschiedene Ansätze für Random Walks vorgestellt. Die Autoren haben sich in ihrer Forschung mit der Methodik zur Identifizierung und Zusammenfassung von Gemeinschaftsstrukturen in Netzwerken sowie mit ihrer Anwendung für die Untersuchung des Verhaltens der verschiedenen Random Walks in synthetischen Benchmark-Netzwerken sowie im Transport- und im Sozialmultiplexnetz.
(Campigotto et al., 2014) haben 2014 das Paper “A Generalized and Adaptive Method for Community Detection” publiziert, aus dem wir die Louvain Methode entnehmen.
Weitere Arbeit die erwähnt werden sollte ist das Paper “A Cooperative Evolutionary Approach to Learn Communities in Multilayer Networks” von (Amelio & Pizzuti, 2014), in dem der Multilayer Genetic Algorithmus im Fokus stand. Daneben wurden das Konzept von Multilayer-Netwerken, genetische Darstellung und Fitness Funktion vorgestellt.
Diese Beiträge sind die Basis unserer Arbeit.
3. Methodik
Alessia Amelio und Clara Pizzuti definieren ein Multilayer-Netzwerk als eine Menge \(\mathcal{N}=\{ \mathcal{N}_1 ,\dots, \mathcal{N}_d \}\) von Slice-Netzwerken. Sei \(V\) eine Menge von \(n\) Objekten. Jeder Slice \(N_s\) kann als Graph \(G_s = (V_s , E_s)\) modelliert werden, wobei die Menge der Knoten \(V_s \subseteq V\) ist die Teilmenge der Objekte von V, die in der Scheibe \(\mathcal{N}_s\) erscheinen, und \(E_s\) ist die Menge der Verbindungen, die die Objekte von \(V_s\) in der s-ten Schicht verbinden, d. h. eine Kante \((u, v) \in E_s\) , wenn die Objekte \(u\) und \(v\) in der \(s\)-ten Schicht interagieren. \(\mathcal{N}\) kann also als eine Menge \(\mathcal{G} = \{ G_1 ,\dots, G_d \}\) von Graphen dargestellt werden, wobei jedes \(G_s = (V_s , E_s )\), für \(s = 1,\dots , d\), das Graphenmodellierungsnetz \(\mathcal{N}_s\) in der s-ten Schicht ist. Eine Schicht stellt somit eine der \(d\) Scheiben des Netzes dar. Bei einem Objekt \(u \in V\) sind die Nachbarn von \(u\) in der Schicht \(s\) definiert als \(n_s(u) = \{ v \in V_s| (u,v) \in E_s \}\), und die Nachbarn von \(u\) in \(\mathcal{G}\) als \(n(u) = \bigcup_{s=1}^{d} n_s(u)\).
Eine Clustering- oder Community-Struktur \(CS_s = \{ C_{s_1}, \dots, C_{s_k} \}\) einer Ebene \(\mathcal{N}_s\) ist eine Aufteilung von \(G_s\) in Gruppen von Knoten, die eine Qualitätsfunktion maximiert. Außerdem wird für jedes Paar von Communities \(C_{s_i}\) und \(C_{s_j} \in CS_s, V_{s_i} \cap V_{s_j} = \emptyset\) (Amelio & Pizzuti, 2014).
4. Algorithmen
4.1 Random Walks
Eine Methode um Gemeinschaften in Multilayer Netzwerken zu ermitteln basiert auf zufälligen Läufen über das Netzwerk. Aufgrund der Definition der Struktur einer Gemeinschaft (viele Verbindungen innerhalb der Gemeinschaft und wenigen Verbindungen nach außen) werden zufällige Läufe welche von einem Knoten innerhalb einer Gemeinschaft starten auch mit hoher Wahrscheinlichkeit in dieser Gemeinschaft bleiben.
Diese Tatsache wird lokal genutzt, um ausgehend von einem gewählten Startknoten zufällige Läufe über das Netzwerk zu machen und so die Gemeinschaft des jeweils gewählten Startknotens zu finden.
Im Folgenden werden wir genauer auf das von (JEUB et al., 2017)
vorgestelle Verfahren eingehen.
4.1.1 Notation
Die Folgende Beschreibung der Notation entspricht der von (JEUB et al., 2017) vorgestellten Notation.
Multilayer Netzwerke werden als \(M(V_M,E_M,V,L)\) beschrieben wobei \(G_M(V_M,E_M)\) ein Graph ist und \(V\) beziehungsweise \(L\) die Menge der Knoten beziehungsweise Layer entspricht. \(V_M\subseteq V\times L\) ist die Menge der Knoten innerhalb der jeweiligen Layer und \(E_M\subseteq V_M\times V_M\) ist dann die Menge aller Kanten innerhalb und zwischen den Knoten aller layer.
Außerdem wird \(i\alpha \in V_M\) genutzt um den Knoten \(i \in V\) in Layer \(\alpha \in L\) zu repräsentieren und \((i\alpha, j\beta)\in E_M\) beschreibt eine gerichtete Kante von \(i\alpha\) nach \(j\beta\).
Der Adjazenztensor \(A\) funktioniert analog zu einer Adjazenzmatrix in einem Einschichtigen Netzwerk und ist wie folgt definiert:
4.1.2 Definition Random Walk
Allgemein lässt sich ein Random Walk auf einem multilayer Netzwerk wie folgt definieren:
\[p_{i\alpha}(t+1)=\sum_{j\beta\in V_M}P^{j\beta}_{i\alpha}p_{j\beta}(t)\]Wobei \(p_{j\beta}(t)\) die Wahrscheinlichkeit angibt sich zum Zeitpunkt \(t\) (zum Beispiel nach \(t\) Schritten) auf dem Knoten \(j\beta\) zu befinden. \(P^{j\beta}_{i\alpha}\) gibt die Wahrscheinlichkeit an für einen Schritt von \(j\beta\) nach \(i\alpha\) an.
Eine mögliche Wahl für \(P\) wäre eine in der alle ausgehenden Kanten eines Knotens gleich behandelt werden, also speziell auch die Kanten innerhalb und zwischen Schichten.
Die Wahrscheinlichkeit \(P^{j\beta}_{i\alpha}\) entspräche dann eins durch geteilt durch die Menge aller von \(j\beta\) ausgehenden Kanten und \(P\) wäre wie folgt definiert:
In ihrer Arbeit (JEUB et al., 2017) gehen die Autoren auf zwei weitere mögliche Definitionen von \(P\) ein, welche wir im Folgenden vorstellen wollen.
4.1.3 Definition Classical Random Walk
Für den Classical Random Walk ist \(P\) wie in 4.1.2 definiert, wobei nur die Definition von \(A\) erweitert wird. Es wird ein neues Gewicht \(\omega\in[0,\infty)\) eingeführt. \(\omega\) ist das Gewicht der Kanten zwischen gleichen Knoten \(i\in V\) in verschiedenen Schichten vor. Es gilt \(A^{i\alpha}_{i\beta}=\omega\) für \(\alpha \neq \beta\).
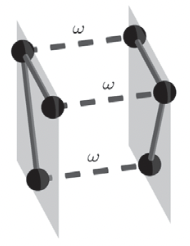 Abbildung 1: Classical Random Walk (JEUB et al., 2017)
Abbildung 1: Classical Random Walk (JEUB et al., 2017)
4.1.4 Definition Relaxed Random Walk
Für den Relaxed Random Walk wird ein Parameter \(r\in[0,1]\) eingeführt. Dieser Paramter gibt die Wahrscheinlichkeit für einen Schritt innerhalb der selben Schicht \((1-r)\) beziehungsweise einer anderen Schicht \((r)\) an.
\[P_{j\beta}^{i\alpha}=(1-r)\delta(\alpha,\beta)\frac{A^{i\alpha}_{j\alpha}}{\sum_{j\in V}A^{i\alpha}_{j\alpha}}+r\frac{A^{i\beta}_{j\beta}}{\sum_{j\in V,\beta\in L}A^{i\beta}_{j\beta}}\]\(\delta\) bezeichnet hier die Kronecker-Delta Funktion, es gilt:
\[\delta(\alpha, \beta)=\bigg \{\begin{matrix}1,\alpha=\beta\\0,\alpha\neq\beta\end{matrix}\]Die Wahrscheinlichkeit für einen Schritt von \(i\) nach \(j\) innerhalb der selben Schicht fällt also weg, falls die Schichten \(\alpha\) und \(\beta\) nicht gleich sind.
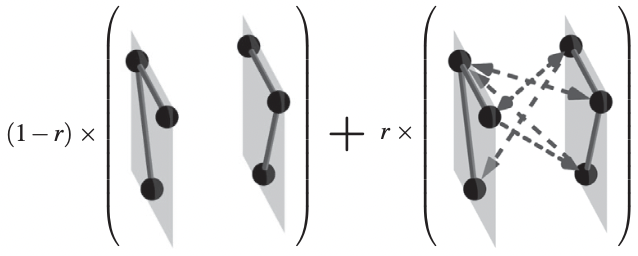 Abbildung 2: Relaxed Random Walk (JEUB et al., 2017)
Abbildung 2: Relaxed Random Walk (JEUB et al., 2017)
4.1.5 Lokale Gemeinschaften
Die Qualität einer Gemeinschaft lässt sich auch viele Arten messen. Eine Methode ist Conductance (Jerrum & Sinclair, 1988). Conductance ist die Größe einer Menge \(S\subset V_M\) welche angibt wie viele Radom Walks auf einem Knoten enden, der sich nicht mehr in der Menge \(S\) befindet.
\[\Phi(S) = \frac{\sum_{i\alpha \in S}\sum_{j\beta\notin S}P^{i\alpha}_{j\beta}p_{i\alpha}(\infty)}{\sum_{i\alpha}p_{i\alpha}(\infty)}\]Extremfälle wären \(\Phi(S)=0\), was bedeutet, dass kein Lauf \(S\) verlässt, \(S\) also von restlichen Netzerk getrennt ist und \(\Phi(S)=1\) wenn kein Lauf innerhalb von \(S\) landet, \(S\) also keine inneren Verbindungen hat.
Mit Hilfe dieser Eigenschaft kann jetzt die optimale Gemeinschaft für einen Knoten \(i\alpha\) definiert werden durch:
Um diese zu finden verwenden (JEUB et al., 2017) in ihrem Paper die ACLcut Methode (ACLcut).
4.2 Louvain Methode
Die Louvain-Methode (Campigotto et al., 2014), deren Name der Louvain-Universität verdankt wird, ist ein Alorithmus, der für sehr große, gewichtete Graphen geeignet ist. Das Ziel der Methode ist ein lokales Maximum eines Moduls zu finden, sodass die Modularität bestimmt werden kann und Gemeinschaften entdeckt, bzw. zusammengefasst werden können.
Der Algorithmus bedient sich an zwei Submethoden: einer Greedy-Optimierungsmethode (siehe One pass algorithm) zur Gruppierung von Knoten zu einer Gemeinschaft durch die Bestimmung des lokalen Maximums, und einer übergeordneten Methode zur Konstruktion eines Metagraphens, der die Gemeinschaften als Knoten enthält (siehe Louvain algorithm).
Die Greedy-Methode schiebt die Knoten eines Graphens, wenn nötig mehrfach, in benachbarte Gemeinschaften, bis dass die Modularität durch das Verschieben nicht mehr erhöht werden kann. Dadurch kann eine Partition des Graphen, also eine Gemeinschaft, zurückgegeben werden.

Die Oberfunktion des Louvain-Algorithmus nimmt als Parameter einen gewichteten Graphen und führt die Greedy-Optimalisierung auf diesen Graphen aus, gefolgt von dem Hinzufügen der resultierenden Partition zum Graphen, sodass ein Metagraph entsteht, dessen Knoten die Gemeinschaften des Ursprungsgraphen sind.

4.2.1 “Multi-slice Modularity”-based Louvain
Um dieses Verfahren zur Gemeinschaftsfindung bei Multilayernetzwerken einzusetzen, hat (Liu et al., 2018) dieses Verfahren durch zwei Schritte erweitert, basierend auf der Verallgemeinerung der Modularität bei mehrschichtigen Netzwerken von (Mucha et al., 2010):
Bei dieser Verallgemeinerung stehen \(i\) und \(j\) für alle Knoten, \(s\) und \(r\) bilden den Bereich aller Schichten und \(C_{jsr}\) beschreibt das Bestehen \((0)\), oder das Nichtbestehen \((w)\) von Verbindungen zwischen den Layern durch einen Binärwert \({0, w}\). Weitere Variablen sind \(K_{is}(K_{js}\)), der den Grad eines Knotens im Layer \(s\) beschreibt, und \(m{_s}\) ist die Anzahl der Kanten im Layer \(s\). \(\gamma_{s}\) dient zur Auflösung und \(\mu\) zur Normalisierung.
Die zwei Erweiterungsschritte zur Anwendung auf Multilayernetzwerke sind wie folgt:
Zunächst wird das lokale Maximum von \(Q_{\text {multi-slice }}\) der aktuellen Ebene des Mulilayernetzwerkes gesucht, wie zuvor beim Optimierungsalgorithmus (siehe One pass) beschrieben, sodass die Knoten Gemeinschaften darstellen.
Der zweite Schritt ist das Berechnen der neuen Gewichte auf der aktuellen Ebene. Die Summe der Gewichte aller Kanten der selben Ebene wird in den neuen Knoten gespeichert.
Die Kante, die zwei Knoten aus verschiedenen Ebenen verbindet, erhält ihren Wert aus den Kanten von jenen Knoten zu anderen Gemeinschaften.
Durch diese Modifikationen lassen sich Gemeinschaften auch auf Multilayernetzwerken finden.
Trotz dessen, dass der Louvain-Algorithmus als klassischer OCDA bekannt ist, zählen wir diese Form des Louvain-Algorithmus unter den neuen Algorithmen auf, da genügend Modifikationen vorhanden sind, die neu sind, wie die Berechnung der Gewichte der Kanten zwischen den Layern, sodass der auf Multilayern laufende Louvain-Algorithmus als neuer Algorithmus deklariert werden kann.
4.3 Multilayer Genetic Algorithm (MultiGA)
MultiGA ist ein evolutionär Algorithmus, welcher in der Lage ist, Overlapping Community-Struktur in Multilayer-Netzwerk zu erkennen. Für MultiGA sind die genetische Repräsentation von Individuen sowie die Fitness Funktion von notwendiger Bedeutung.
In der nachfolgenden Beschreibung werden wir näher auf die genetische Repräsentation, die Fitness Funktion und schließlich auf das von (Amelio & Pizzuti, 2014) vorgestelle Verfahren eingehen.
4.3.1 Genetische Repräsentation und Operation
Das Konzept der von diesem Verfahren verwendeten genetischen Repräsentation basiert stark auf die Idee der locusbasierten Adjazenzarstellung. (Amelio & Pizzuti, 2014) beschreiben ein Individuum wie folgt:
Ein Individuum \(I=\{ I_1,\ldots ,I_d\}\) der Polulation besteht aus einer Menge von d Elementen \(I_s\), \(1 \leq s \leq d\). Jedes Element \(I_s\) besteht aus n Genen \(g_1,\ldots ,g_n\), die als ganzzahlige Werte im Bereich \(\{ 1,\ldots ,n \}\) angenommen werden, die den Netzwerkknoten entsprechen. Ein Wert \(v\), der dem \(u\)-ten Gen zugeordnet ist, bedeutet, dass es eine Verbindung zwischen den Knoten \(u\) und \(v\) im \(s\)-ten Graphen \(G_s\) gibt, der die \(s\)-te Netzwerkschicht \(\mathcal{N}_s\) modelliert. Wenn der Knoten \(u\) keine Verbindungen in der \(s\)-ten Schicht hat, d. h. \(n_s(u) = \emptyset\), dann wird ihm ein Nullwert zugewiesen. Somit ergibt jedes Element \(I_s\) eines Individuums \(I\) der Population eine Unterteilung der \(s\)-ten Schicht \(\mathcal{N}_s\) von \(\mathcal{N}\) in eine Anzahl \(c_s\) von Communities.
Der Initialisierungsprozess betrachtet für jedes Individuum \(I = \{ I_1,\ldots , I_d\}\) alle Elemente \(I_s\) und weist einem Knoten \(u\) zufällig einen seiner Nachbarn \(v\) zu, wobei \(v \in n_s(u)\), d. h. einer der Nachbarknoten von \(u\) in Bezug auf den der \(s\)-ten Schicht entsprechenden Graphen \(G_s\) ist. Wenn \(u\) keine Nachbarn in \(G_s\) hat, dann ist das entsprechende Gen \(g_u = 0\).
4.3.2 Fitness Funktion
Um die Idee einer dichten Menge von Knoten zu interpretieren ist das Konzept der Modularität für Single-Layer-Netzwerke von (Newman & Girvan, 2004) nützlich:
\[Q=\frac{1}{2m}\cdot {\sum}_{ij} (A_{ij} - \frac{k_ik_j}{2m})\delta (C_i, C_j)\],wobei A die Adjazenzmatrix des zugehörigen Graphen ist, m die Anzahl der Kanten des Graphen, \(k_i\) und \(k_j\) die Grade der Knoten \(i\) bzw. \(j\) sind. \(\delta\) ist die Kronecker-Funktion und ergibt 1, wenn \(i\) und \(j\) im gleichen Community sind (d. h. \(C_i =C_j\)), andernfalls Null. Werte, die sich 1 nähern, weisen auf eine hohe Qualität der Clusterbildung hin (Amelio & Pizzuti, 2014).
Anhand der Definition der Modularität Q von (Newman & Girvan, 2004) erweitern die Autoren das Konzept der Modularität auf Multilayer-Netzwerke. Die für jede Schicht berechneten Modularitätswerte werden so kombiniert, dass der Wert für jede Schicht durch die Werte aller anderen Schichten beeinflusst wird (Amelio & Pizzuti, 2014). Seien \(s\) und \(r\) zwei Schichten eines Multilayer-Netzwerks und \(CS_s\), \(CS_r\) die für die Netze \(\mathcal{N}_s\) bzw. \(\mathcal{N}_r\) erhaltenen Clustering-Werte. Dann ist die kombinierte Modularität \(Q_{sr}\) zwischen den Schichten \(s\) und \(r\) wie folgt definiert (Amelio & Pizzuti, 2014):
\begin{align}
Q_{sr}=\frac{1}{2m_s + 2m_r}\cdot \sum_{ij} [(A_{ijs} - \frac{k_{is}k_{js}}{2m_s})\delta (C_{is}, C_{js}) + (A_{ijr} - \frac{k_{ir}k_{jr}}{2m_r})\delta (C_{is}, C_{js}) \ \ \ \ (1)
\end{align}
,wobei \(A_s\) und \(A_r\) die Adjazenzmatrizen der Graphen \(G_s\) bzw. \(G_r\) sind, \(k_{is}\) und \(k_{js}\) die Grade der Knoten \(i\) und \(j\) in \(G_s\) sind, während \(k_{ir}\) und \(k_{jr}\) die Grade der Knoten \(i\) bzw. \(j\) in \(G_r\) sind. Die Kronecker-Funktion \(\delta\) ergibt 1, wenn \(i\) und \(j\) im gleichen Community \(C_s\) sind (d. h. \(C_{is} = C_{js}\)), andernfalls Null. Die Bedeutung von \(Q_{sr}\) besteht darin, dass bei der Berechnung einer Gemeinschaftsstruktur \(CS_s\) auf Slice \(\mathcal{N}_s\) diese Gemeinschaftsstruktur auch auf Slice \(\mathcal{N}_r\) geprüft wird. Wenn \(CS_s\) also keine gute Gruppierung von Knoten auch in \(N_r\) bestimmt, wird es benachteiligt, weil der zweite Term von Formel (1) niedrig ist.
Analog dazu ist die kombinierte Modularität \(Q_{rs}\) zwischen den Slices \(r\) und \(s\) definiert als
\begin{align}
Q_{rs}=\frac{1}{2m_s + 2m_r}\cdot \sum_{ij} [(A_{ijr} - \frac{k_{ir}k_{jr}}{2m_r})\delta (C_{ir}, C_{jr}) + (A_{ijs} - \frac{k_{is}k_{js}}{2m_s})\delta (C_{ir}, C_{jr})] \ \ \ \ (2)
\end{align}
Durch Summieren der kombinierten Modularitäten \(Q_{sr}\) für jedes Paar Scheiben \(s\) und \(r\) ergibt sich die gesamte kombinierte Modularität \(Q_{ml}\) auf allen \(d\) Scheiben:
\begin{align}
Q_{ml} = \sum_{s, r s \neq r}(Q_{sr}+Q_{rs}) \ \ \ \ (3)
\end{align}
4.3.3 Der Algorithmus
Die Idee hierbei ist, dass bei der Erkennung einer Community-Struktur \(CS_s\) auf einer Ebene \(s\) die Ähnlichkeit zwischen Ebene s und anderer Ebenen \(r (r \neq s)\), \(r = 1, \cdots , d\) , berücksichtigt wird. Die Ähnlichkeit bedeutet hier, dass \(CS_s\) und \(CS_r\) dieselbe Gruppe von Knoten erhalten.
 Abbildung 5: MultiGA Method (Amelio & Pizzuti, 2014)
Abbildung 5: MultiGA Method (Amelio & Pizzuti, 2014)
Der MultiGA-Algorithmus wird in Abbildung 5 beschrieben. Als Eingabe erhält er ein Multilayer-Netzwerk \(\mathcal{N}\) von \(d\) Dimensionen und die Menge der Graphen \(\mathcal{G} = (G_1, \dots , G_d)\), die es modellieren. Die Ausgabe ist eine Knoten-Cluster-Beschriftung L, die \(\mathcal{N}\) in die optimale gemeinsame Gemeinschaftsstruktur unterteilt.
Schritt 1: Eine zufällige Population von Individuen \(I = \{ I_1, \cdots , I_d\}\) wird erzeugt.
Schritt 2: Eine feste Anzahl von Generationen wird entwickelt.
Schritt 3: Für jedes Individuum \(I\) in der Population wird die gesamten kombinierten Modularität \(Q_{ml}\) (anhand der Formel (3)) berechnet.
Schritte 4-9: Für jedes Element \(I_s\) von \(I\) wird die kombinierte Modularität von \(I_s\) mit allen anderen Schichten berechnet.
Schritt11: Eine neue Population wird durch Anwendung der Variationsoperatore erzeugt.
Schritte 13-17: Für jede Schicht wird ein Knotenetikettenvektor \(L_s\) erzeugt. Das bedeutet, dass jedem Knoten \(v_i\) durch die Clustering-\(CS\) das Etikett der Gemeinschaft zugewiesen wird.
Im Fall, dass ein Knoten \(u\) in der Schicht \(s\) keinem Cluster zugewiesen wurde, weil er keine Verbindungen zu den Knoten dieser Schicht hat, stellen (Amelio & Pizzuti, 2014) die LabelAssignment-Methode (Abbildung 5(b)) wie folgt vor:
Schritte 2-5 der LabelAssignment-Methode: \(u\) wird das Cluster-Label zugewiesen, das am häufigsten in den \(CS_s\) seiner gesamten Nachbarn vorkommt.
Schritte 20-21: Für jede Schicht \(s\) wird nun der Modularitätswert \(G\) von (Newman & Girvan, 2004) in Bezug auf die durch \(L_s\) bestimmte Partitionierung berechnet. Das Labeling \(L_s\) wird so gewählt, dass das den maximalen Q-Wert ergibt.
Schritt 22: Eine lokale Suche, ähnlich der von (Blondel et al., 2008) vorgeschlagenene Methode, wird auf dem Graphen \(\bar{\mathcal{G}} = \bigcup_{s=1}^d G_s\) durchgeführt.
6. Zusammenfassung
Das Konzept der Modulatität ist sehr nützlich bei der Erkennung von Communities. Allerdings hat es noch viele Nachteile, was die treibende Kraft hinter der Entwicklung der Louvain Methode und dem Multilayer Genetic Algorithm (MultiGA) ist.
Das Ziel der Louvain Methode ist die Modularitätsmaximierung, die den Unterschied zwischen der tatsächlichen und der erwarteten internen Verbindungsdichte in Communities misst (Campigotto et al., 2014). Dies ermöglicht die Bewertung der Qualität von Aufteilungen in Communities. Außerdem wird die Qualität der Partitionen verbessert, da sich verschiedene Arten von Communities mithilfe der Louvain Methode finden lassen. MultiAG erweitert nicht nur das Modularitätskonzept, sondern benutzt auch die genetische Darstellung von Individuen in Multilayer-Netwerken. Darüber hinaus wird die Ergebnisqualität vom MultiGA durch die lokale Suchstrategie verfeinert.
Im Gegensatz zu den beiden oben genannten Methoden wird beim Algorithmus Random Walks das Verhalten der Gruppen von Knoten (Communities) bei der Ausbreitung eines dynamischen Prozesses in einem Netzwerk analysiert. Viele unterschiedliche Engpässe, d.h viele Gruppen von Knoten, werden dadurch gebildet und dadurch ist die Aufteilung des Netzwerks zu finden.
Es lässt sich festhalten, dass die in unserer Arbeit vorgestellten neuen Algorithmen für die Entdeckung und Analyse von Communities in Multilayer-Netzwerken geeignet sind.
7. Referenzen
- Multilayer networks. (2014). Journal of Complex Networks, 2(3), 203–271. https://doi.org/10.1093/comnet/cnu016
- JEUB, L. U. C. A. S. G. S., MAHONEY, M. I. C. H. A. E. L. W., MUCHA, P. E. T. E. R. J., & PORTER, M. A. S. O. N. A. (2017). A local perspective on community structure in multilayer networks. Network Science, 5(2), 144–163. https://doi.org/10.1017/nws.2016.22
- Amelio, A., & Pizzuti, C. (2014). A Cooperative Evolutionary Approach to Learn Communities in Multilayer Networks. Parallel Problem Solving from Nature – PPSN XIII, 222–232. https://doi.org/10.1007/978-3-319-10762-2_22
- Jerrum, M., & Sinclair, A. (1988). Conductance and the rapid mixing property for Markov chains: the approximation of permanent resolved. Proceedings of the Twentieth Annual ACM Symposium on Theory of Computing - STOC ’88. https://doi.org/10.1145/62212.62234
- Liu, W., Suzumura, T., Ji, H., & Hu, G. (2018). Finding overlapping communities in multilayer networks. PLOS ONE, 13(4), e0188747. https://doi.org/10.1371/journal.pone.0188747
- Mucha, P. J., Richardson, T., Macon, K., Porter, M. A., & Onnela, J.-P. (2010). Community Structure in Time-Dependent, Multiscale, and Multiplex Networks. Science, 328(5980), 876–878. https://doi.org/10.1126/science.1184819
- Newman, M. E. J., & Girvan, M. (2004). Finding and evaluating community structure in networks. Physical Review E, 69(2), 026113.
- Blondel, V. D., Guillaume, J.-L., Lambiotte, R., & Lefebvre, E. (2008). Fast unfolding of communities in large networks. Journal of Statistical Mechanics: Theory and Experiment, 2008(10), P10008. https://doi.org/10.1088/1742-5468/2008/10/p10008