Emilio Rolandi
RWTH Aachen University
emilio.rolandi@rwth-aachen.de
Fynn Haller
RWTH Aachen University
fynn.haller@rwth-aachen.de
David Brenn
RWTH Aachen University
david.brenn@rwth-aachen.de

Abstract

Multilayer-Netzwerke haben aufgrund von Social-Media und des Internets in den letzten Jahren stark an Bedeutung gewonnen. Die Freundesgruppen in Facebook, Follower-Netzwerke in Twitter, sowie Chatgruppen in WhatsApp lassen sich dadurch akkurat repräsentieren. Im Vergleich zu Netzwerken mit nur einer Ebene lassen sich Multilayer Netzwerke nur schwerer durch klassische Darstellungsmethoden wie Graphen und Adjazenz-Matrizen repräsentieren. Diese können nämlich nicht die enorme Komplexität bewältigen, die moderne Netzwerke enthalten sowie die rasante Modifikation der Gruppen, Verbindungen, usw. Deshalb werden wir im Folgenden verschiedene mathematische Repräsentationen vorstellen und sie gegeneinander abwägen. Was für Vorteile hat jede Repräsentation und für welche Anwendungsfälle ist welche Darstellung am besten geeignet. Wir werden uns vor allem auf soziale Netzwerke konzentrieren, die sich auf Relationen zwischen Menschen konzentrieren, um die beste Methode zu ermitteln und diese darzustellen. Diese Arbeit soll eine Grundlage, um zukünftigen wissenschaftlichen Arbeiten bei der Wahl von passender Repräsentation zu helfen. Unsere Schlussfolgerung ist, dass es kein Modell gibt das für jeden Anwendungsfall am besten geeignet ist. Jedes hat seine Vor- und Nachteile und ist somit für bestimmten Anwendungen besser geeignet. Die Supraadjazenzmatrix ist jedoch allgemein effizienter für grundelegnde Operationen.

Inhaltsverzeichnis

  1. Einleitung
  2. Verwandte Arbeiten
  3. Methodik
    1. Multilayer Netzwerke
      1. Allgemeine Repräsenation Modell 1
      2. Allgemeine Repräsenation Modell 2 Multiaspects
    2. Supraadjazenzmatrix für allgemeine Multilayer Netzwerke
      1. Muliplex Netzwerke
      2. Mulislice Netzwerke
      3. Implementierungen aus der Adjazenzmatrix
    3. Vergleich
  4. Zusammenfassung
  5. Referencen



1. Einleitung

In der Natur wie auch in unseren sozialen Strukturen tauchen unterschiedlichste Verbindungen auf. Sein es die direkte Beziehung zwischen Freunden oder aber auch die Interaktionen zwischen Menschen auf verschiedenen sozialen Netzwerken. Diese Netzwerke werden oft mit Graphen modelliert. Wobei wir in dieser Arbeit zwischen klassischen (Einer Ebene) und modernen (Multilayer) Netzwerken unterscheiden werden. Einen klassischen Graph wird definiert als ein Tupel \(G = (V,E)\) bestehend aus einer Menge \(V\) von Knoten und \(E\) von Kanten. Dabei gilt, das ein Tupel der Form \((v,u) \in E\) existiert genau dann wenn, es eine Verbindung zwischen zwei Knoten \(u,v\) gibt. Dies könnte beispielsweise symbolisieren, das eine Person u eine Person v auf Instagram folgt.

Bei komplexeren und informationsreicheren Systemen reicht diese Repräsentationsmethode nicht aus, da man unterschiedliche Eigenschaften in Betracht ziehen möchtet. Viele Informationen würden verloren gehen, wenn man solche Systeme mit ein klassisches Netzwerk darstellen will. Wenn man beispielsweise die Evolution des Netzwerkes über eine Zeitperiode untersuchen will, und nicht nur zu einem bestimmten Zeitpunkt. All diese Informationen in nur einer Ebene zu vereinen würde zu einem sehr unübersichlichen und nicht mehr brauchbares Netzwerk führen.

Um die Information beizubehalten, verwenden wir eine komplexere Repräsentationsmethode, nämlich die Multilayer-Netzwerke. Einen Multilayer-Netzwerk ist eine Komposition aus mehrere Netzwerke. Jede Ebene des Mutlilayer-Netzwerk entspricht einem eigenen Netzwerk. Dabei sind Verbindungen zwischen Knoten aus unterschiedlichen Ebenen möglich. Wir erlauben also Verbindungen zwischen einzelnen Netzwerken zu einem großen Multilayer-Netzwerk.

Ein Beispiel wo diese Darstellungsmethode geeignet ist, sind Sozialnetzwerke. Angenommen man möchte die Kommunikation zwischen Communitys in Abhängigkeit von den genutzten Kommunikationsplattformen analysieren. Die einzelnen Plattformen können hierbei als verschiedene Ebenen dargestellt werden und zusammen in einem Multilayer-Netzwerk repräsentiert werden.

Für die unterschiedlichsten wissenschaftlichen Bereiche die komplexe Netzwerke nutzen, kann es sinnvoll sein, Eigenschaften von Multilayer-Netzwerk zu untersuchen. Zum Beispiel, wenn die Patner von unterschiedlichen Ländern in einem Multilayer-Netzwerk dargestellt werden. Wobei eine Ebene die militärischen Allianzen und eine andere Ebene wirtschaftliche Abkommen darstellt. Dabei konnte man sich Fragen, wie stark die Korrelation zwischen beiden Ebenen sind. Also inwiefern neigen Ländern mit ähnliche kommerzielle Ziele auch ähnliche militärische Ziele zu haben.

Um solche Zusammenhänge zu berechnen, reicht es jedoch nicht aus, nur das abstrakte Konzept einer Multilayer-Netzwerk zu verstehen, sondern man muss es mathematisch konkret repräsentieren.

Damit werden wir uns in Folgenden beschäftigen. Dazu betrachten wir verschiedene Typen von Multilayer-Netzwerken und geben die Unterschiede der verschiedenen Repräsentationsmöglichkeiten an.

Wir werden uns mit drei Möglichkeiten befassen:

Allgemeine Repräsentation Modell 1, allgemeine Repräsentation Modell zwei, und Supraadjazenzmatrizen. Zum Schluss werden wir alle Modelle vergleichen.

2. Verwandte Arbeiten

Diese Arbeit untersucht die verschiedenen Repräsentationsmöglichkeiten aus den folgenden Arbeiten. Dabei werden wir uns genauer die Modelle der Arbeiten “Multilayer networks”(Kivela et al., 2014) und “Multilayer networks: Structure and function” (Bianconi, 2018) betrachten und vorstellen. “Multilayer networks”(Kivela et al., 2014) ist eine der ältesten Arbeiten und setzt somit eine der Grundlagen der Multilayer Definition. “Multilayer networks: Structure and function”(Bianconi, 2018) versucht, mit so wenig Termen wie möglich Multilayer-Netzwerken zu beschreiben und zu klassifizieren, sie liefert somit einen anderen Blickwinkel. Diese beiden Werke werden genutzt, um die allgemeine mathematische Repräsentation zu untersuchen. “The structures and dynamics of Multilayer-networks” (Boccaletti et al., 2014) bietet Materialien für die Visualisierung von unterschiedlichen Darstellungsmöglichkeiten. Außerdem ist es aus dem Jahr 2014 und hat somit bei der Forschung einige Netzwerke in Betracht gezogen, die vor einige Jahrzehnten nicht existierten. “What is … a Multilayer Network” (Porter, 2018) fokussiert sich insbesondere auf die Supraadjazenzmatrix, eine bestimmte Darstellungsmöglichkeit für Multilayer-Netzwerke, und liefert uns noch dazu unterschiedliche Netzwerkarten, die sich mit einer Multilayer-Netzwerk darstellen lassen. “An introduction to Multilayer Networks” (Marcello Tomasini, 2015) erläutert klassische Repräsentationsmöglichkeiten für Multilayer-Netzwerke und beschreibt außerdem unterschiedliche Eigenschaften eines Multilayer-Netzwerks. Da die Multilayer-Netzwerke informationsreicher sind, kann dies auch Nachteile haben. Der Aufwand einiger Probleme kann sich deutlich erhöhen. Solche Probleme und ihre Lösungsmöglichkeiten werden in “Lifting the curse of dimensionality erklärt. “Role of the adjacency matrix in Graph-theory” (Kuo & Sloan, 2005) erklärt die Vor- und Nachteile, die die Adjazenzmatrix im Vergleich zu anderen Repräsentationsmöglichkeiten hat. Diese Arbeit dient als Inspiration, um die Supraadjazenzmatrix mit allgemeine Repräsentationsmethode zu vergleichen. Schließlich wird in “powers of the adjacency matrix” (Duncan, 2004) eine Anwendung der Adjazenzmatrix erklärt. Wir haben uns auf dieser Basis eine Anwendung der Supraadjazenzmatrix überlegt.

3. Methodik

3.1 Multilayer-Netzwerke

Um besser mit Multilayer-Netzwerken arbeiten zu können, wird zwischen verschiedenen Typen unterschieden. Dies dient dazu, um für jede Kategorie von Netzwerken ein am besten passendes Repräsentationsmodell zu definieren. Im Folgenden werden wir die verschiedenen Typen und deren mathematische Definitionen erklären und anhand von Beispielen die Anwendungsmöglichkeiten präsentieren (Bianconi, 2018).

3.1.1 Allgemeine Repräsentation Modell 1

Dieses Modell bietet zunächst eine grundlegende Definition, mit der alle Arten von Multilayer-Netzwerke beschrieben werden können.

Wir stellen erst die Definition aus Ginestra Bianconi (Bianconi, 2018) vor und anschließen die Definition von Kivela M. (Kivela et al., 2014). Es fällt aus dass obwohl beide Repräsentationsmöglichkeiten für alle Multilayer-Netzwerke gedacht sind, es dennoch Unterschiede in der Struktur der mathematischen Definition gibt und somit beide als Grundlage dienlich sind.

Multilayer-Netzwerke nach: Ginestra Bianconi (Bianconi, 2018)

Ein Multilayer-Netzwerk lässt sich definieren als ein Triplet

\[\mathcal{M} = (Y,\vec{G},\mathcal{G})\]

Wobei \(Y\) die Ebenen, \(\vec{G}\) jeweils die Kanten in einer Ebene und \(\mathcal{G}\) die Kanten zwischen den Ebenen darstellt.

Die Ebenen werden als Zahl repräsentiert, wobei \(M\) die Anzahl von Ebenen ist. \(Y\) ist also eine Menge von Ebenen mit:

\[Y = \{\alpha| \alpha \in \{1,2,...M\}\}\]

\(\vec{G}\) ist eine geordnete Liste von Netzwerken, welche die Interaktion von Kanten und Knoten in einer Ebene charakterisiert(Bianconi, 2018).

Für jede Ebene \(\alpha\) gibt es also einen Graphen \(G_\alpha\) welche alle zusammengefasst werden in der Liste \(\vec{G}\)

\[\vec{G} = (G_1,G_2,...,G_\alpha,...,G_M)\]

Die einzelnen Graphen jeder Ebene (missing reference).

Zuletzt fehlt noch die Definition für \(\mathcal{G}\). Hierbei handel es sich wieder um eine Liste von Netzwerken, welche die Verbindungen zwischen den einzelnen Ebenen darstellt. Für jedes Paar von Ebenen \(\alpha,\beta\) mit \(\alpha \beta\) gibt es ein bipartiten Graphen (missing reference).

Betrachten wir nun ein Beispiel. Gegeben ist ein Multilayer-Netzwerk mit ungerichteten und ungewichteten Kanten, das wie folgt aussieht:

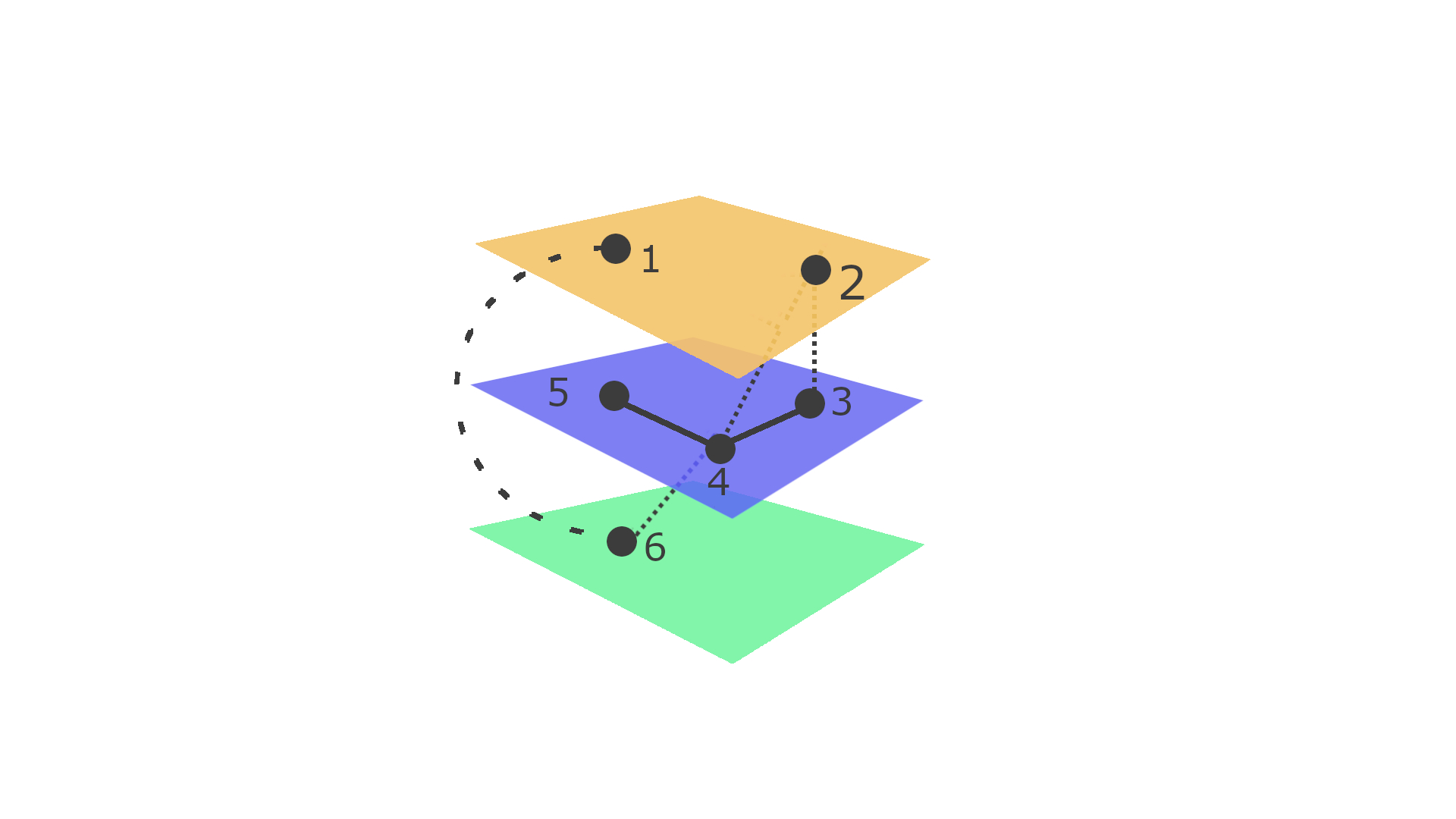Ungerichtetes und ungewichtetes Multilayer-Netzwerk

Dann lässt sich \(M_B\) beschreiben als \(M_B = (Y_B,\vec{G}_B,\mathcal{G}_B)\)

Mit

  • \(Y_B = \{1,2,3\}\), da \(M_B\) 3 Ebenen umfasst
  • \(\vec{G}_B = (G_{B1},G_{B2},G_{B3})\) Die Liste ergibt sich daraus, dass es für jede Ebene einen Graphen \(G_{B\alpha}\) gibt
  • \(\mathcal{G}_B = (G_{1,2},G_{1,3},G_{2,3})\) Für jedes Paar von Ebenen einen Graphen

Wobei die Graphen der Ebenen definiert sind als:

  • \(G_{B1} = (V_1,E_1)\), mit \(V_1 = \{1,2\}, E_1 = \{\}\)
  • \(G_{B2} = (V_2,E_2)\), mit \(V_2 = \{3,4,5\}, E_2 = \{(3,4),(4,3)(4,5),(5,4)\}\)

  • \(G_{B3} = (V_3,E_3)\), mit \(V_3 = \{6\}, E_3 = \{\}\) Die Graphen \(G_{\alpha,\beta}\) zwischen den Ebenen:

  • \(\mathcal{G}_{1,2} = (V_1,V_2,E_{1,2})\), mit \(E_{1,2} = \{(2,3),(3,2),(2,4),(4,2)\}\)
  • \(\mathcal{G}_{1,3} = (V_1,V_3,E_{1,3})\), mit \(E_{1,3} = \{(1,6),(6,1)\}\)
  • \(\mathcal{G}_{2,3} = (V_2,V_3,E_{2,3})\), mit \(E_{2,3} = \{(4,6),(6,4)\}\)

3.1.2 Allgemeine Repräsentation Modell 2 Multiaspects

Im Folgenden werden wir nun die Repräsentationsweise aus (Kivela et al., 2014) darstellen und somit den Hauptunterschied zu der vorherigen Methode aufzeigen. Es handelt sich hierbei ebenfalls um ein generelles Modell für Multilayer-Netzwerke. Es soll so viele verschiedene Arten von Multilayer-Netzwerken umfassen wie möglich. Hierzu wird es so definiert, dass jeder Knoten, mit jedem anderen Knoten des Netzwerkes über eine Kante verbunden sein darf. Dabei ist es egal, auf welcher Ebene der Knoten sich befindet (Kivela et al., 2014). Das Multilayer-Netzwerk besteht aus mehreren Aspekten d, die alle durch eine Menge von “elementary layers” (Kivela et al., 2014) beschrieben werden L. Es gilt: \(L=\{L_a\}_{a=1}^{d}\)

Eine “elementary layer” ist somit eine instance des übergeordneten Aspektes. Aus der Kombination dieser Mengen erhält man die Layers des Multilayer-Netzwerkes. Hierbei werden alle möglichen Tupel aus den “elementary layers” gebildet, so ergeben zum Beispiel die Aspekte \(L_1=\{Facebook,Instagram\}\) und \(L_2=\{2020,2021\}\) die layers \((Facebook,2020),(Instagram,2020),(Facebook,2021)\) und \((Instagram,2021)\).

Ein Multilayer-Netzwerk lässt sich somit, durch ein Quadruplet der Form

\(M= (V_M,E_M,V,L)\) darstellen. (Marcello Tomasini, 2015) Hierbei entspricht V der Anzahl an Knoten in dem Netzwerk und hat die Form:

\(V=\{v_1,...,v_n\}\) \(V_M\) repräsentiert die Menge an “node-layers” (Kivela et al., 2014) des Multilayer-Netzwerkes. Ein “node-layer” gibt an, auf welchen Layers sich ein Knoten befindet. Sie haben die Form:

\[V_M = V \times L_1 \times ... \times L_d\]

Es ergibt sich also ein Tupel: \((a,l) := (a,l_1,...,l_d)\) bestehend aus dem Knoten a und den layers \(l_1,...,l_d\) auf denen sich der Knoten befindet (Kivela et al., 2014).

\(E_M\) repräsentiert die Menge an Kanten zwischen den verschiedenen Knoten und Layern. Sie werden repräsentiert durch die Gleichung:

\(E_M = V_M \times V_M\)(Marcello Tomasini, 2015) Es ergeben ich Tupel der Form: \((a,b)\)

bestehend aus den Beiden Knoten a und b, welche die Kante verbindet (Kivela et al., 2014).

Weiterhin erlaubt dieses Modell sowohl gerichtete, als auch ungerichtete Graphen. Es lassen sich somit gerichtete und ungerichtete Multilayer-Netzwerke darstellen.

Das Modell erlaubt keine Selbstverweisungen also \(((a,b),(a,b)) \notin E_M\), dies muss aber nicht immer der Fall sein und kann, wenn es für ein gegebenes Multilayer-Netzwerk sinnvoll ist, erlaubt werden.

Weiterhin werden die Kanten unterteilt in Kanten, die sich zwischen Layers erstrecken, genannt inter-layer := \(E_C\) und Kanten die nur auf einem Layer sich erstrecken, genannt intra-layer := \(E_A\) (Kivela et al., 2014).

Eine Kante gilt als intra-layer, wenn es gilt:

\[((a,l),(b,j)) \in E_M \vert l=j\]

Somit gilt für die inter-layer Kanten:

\(E_C = E_M \backslash E_M\) (Kivela et al., 2014).

Beispiel Netzwerk:

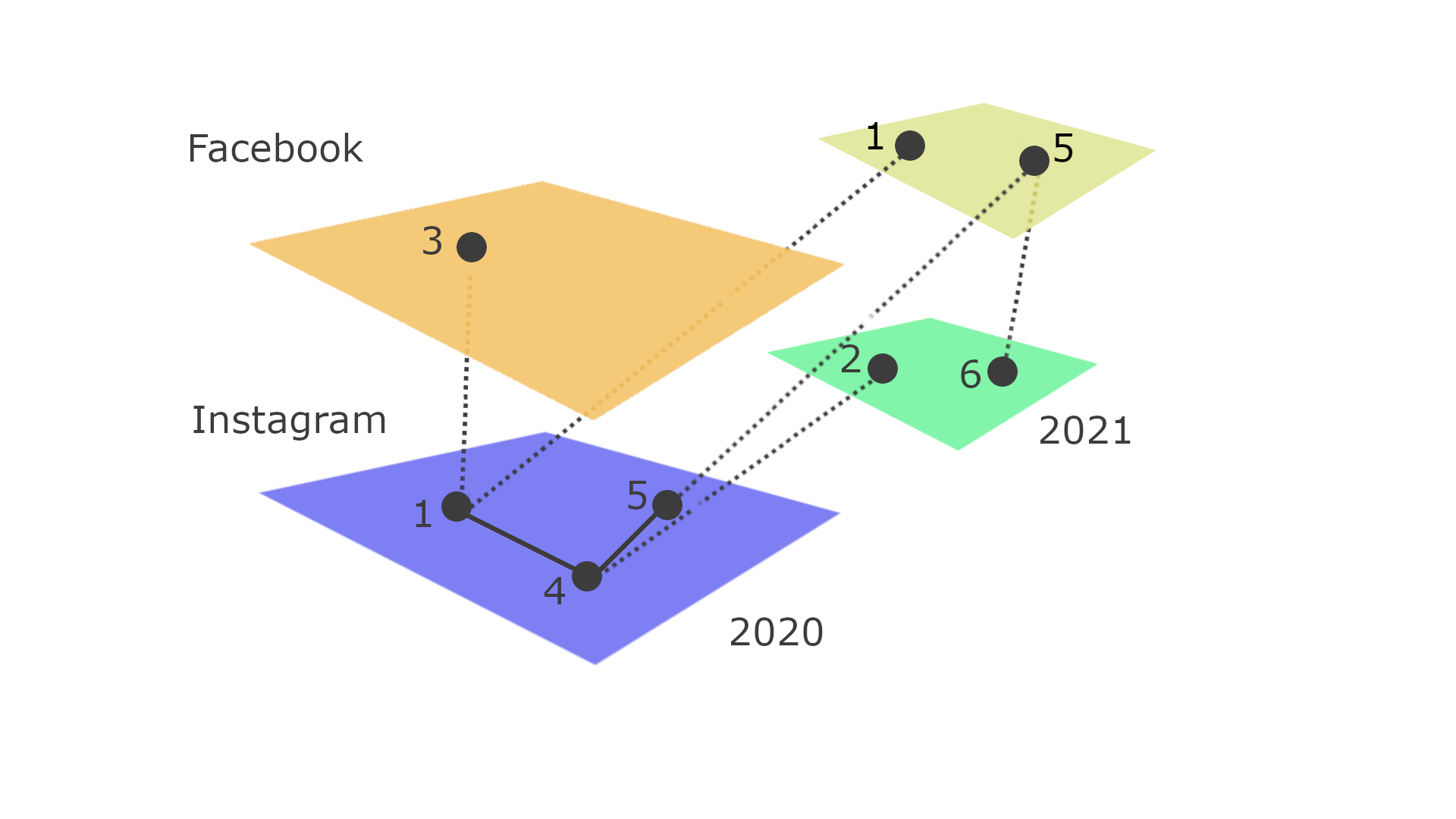Ungewichtetes und ungerichtetes Multilayer-Netzwerk

Instagram wird im Folgenden durch Insta abgekürzt.

\(V_m\) ergibt sich, in dem man die Layers der reihe nach durchgeht und wie oben definiert, den jeweiligen Knoten auf den Layers, in Kombination mit den elementary-layers angibt.

\[V_M = \{(3,Facebook,2020), (1,Facebook,2021), (5,Facebook,2021), \\(1,Insta,2020), (4,Insta,2020), (5,Insta,2020), (2,Insta,2021), (6,Insta,2021)\}\]

\(E_M\) muss, da wir einen ungerichteten Graphen betrachten muss \(E_M\) jede Kante in beide Richtungen beinhalten. Gehen wir nun nach definition vor und weisen jeder Kante ein Tupel \(V_M x V_M\) zu, bestehen aus den beiden Knoten, welche die Kante verbindet. Es ergibt sich:

\[E_M = \{((3,Facebook,2020),(1,Insta,2020)), ((1,Insta,2020),(3,Facebook,2020)), ((1,Facebook,2021),(1,Insta,2020)),\\ ((1,Insta,2020),(1,Facebook,2021)), ((5,Facebook,2021),(5,Insta,2020)), ((5,Insta,2020),(5,Facebook,2021)), \\ ((5,Facebook,2021),(6,Insta,2021)), ((6,Insta,2021),(5,Facebook,2021)),((1,Insta,2020),(4,Insta,2020)), \\ ((4,Insta,2020),(1,Insta,2020)), ((4,Insta,2020),(5,Insta,2020)),((5,Insta,2020),(4,Insta,2020)), \\ ((4,Insta,2020),(2,Insta,2021)), ((2,Insta,2021)(4,Instag,2020)) \}\] \[V = \{1,2,3,4,5,6\}\]

L besteht aus den einzelnen Aspekten des Multilayer-Netzwerkes. In diesem Fall sind dies die Zeit und die Sozial-Media Seite. Es ergeben sich also \(L_1\) und \(L_2\) mit: \(L = \{L_1,L_2\}\) \(L_1 = \{Facebook,Instagram\}\) \(L_2=\{2020,2021\}\)

3.2 Supraadjazenzmatrix für allgemeine Multilayer Netzwerke

Bei den schon erwähnten klassischen Netzwerken wird die Adjazenzmatrix als Repräsentationsmöglichkeit verwendet. Dabei wird für einen Graphen mit n Knoten eine Matrix A der Dimension (nxn), mit

\[A_{ij}=\begin{cases} 1, \text{falls es eine Verbindung von Knoten i nach Knoten j gibt} \\ 0, sonst. \\ \end{cases}\]

Diese Matrix kann man erweitern, um einen Multilayer-Netzwerk darzustellen. Diese Matrix wird Supraadjazenzmatrix gennant. Bei dieser Repräsentationsarten wird das Multilayer-Netzwerk abgeflacht. In den Diagonalblöcken der Matrix werden die Intrakanten gespeichert (Kanten zwischen Knoten derselben Ebene), und in den nicht-diagonale Blöcken werden die Interkanten (Kanten zwischen Knoten aus unterschiedlichen Ebenen) gespeichert. (Porter, 2018)

Die Matrix hat folgende Form:

\(A = \begin{pmatrix} a^{[1,1]} & | & a^{[1,2]} & | & ... & | & a^{[1,M]}\\ ---- & & ---- & & ---- & & ---- \\ a^{[1,2]} & | & a^{[2,2]} & | & ... & | & a^{[2,M]} \\ ---- & & ---- & & ---- & & ---- \\ ... & | & ... & | & ... & | & .... \\ ---- & & ---- & & ---- & & ---- \\ a^{[1,M]} & | & a^{[2,M]} & | & ... & | & a^{[M,M]} \\ \end{pmatrix}\) (Bianconi, 2018)

Wobei

\[A_{ij}^{[a, β]}=\begin{cases} 1, \text{falls (i,a) mit (j,β) verbunden ist} \\ 0, \text{sonst.} \\ \end{cases}\]

Kleines ungewichtetes und ungerichtetes Multilayer-Netzwerk

\[A = \begin{pmatrix} 0 & 0 & 1 & 0 & | & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & | & 0 & 1 & 0 & 0\\ 1 & 0 & 0 & 1 & | & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & | & 0 & 0 & 0 & 0\\ - & - & - & - & - & - & - & - & -\\ 0 & 0 & 0 & 0 & | & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & | & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & | & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & | & 0 & 0 & 0 & 0\\ \end{pmatrix}\]

Einen Graphen und seine Supraadjaenzmatriz.

In der oberen linken Ecke sieht man die Adjazenzmatrix der Ebene 1 (Instagram) (\(a_{[1,1]}\). In der unteren rechten Ecke sieht man die Adjazenzmatrix der Ebene 2 \(a_{[2,2]}\). In der oberen rechten Ecke sieht man die Matrix \(a_[1,2]\) Diese hat eine 1 nur an der Stelle 1,2, weil nur Knoten 1 aus der ersten Matrix mit dem Knoten 2 aus der zweiten Matrix verbunden ist. Es ist wichtig zu beachten, das es sich hier nicht um eine große Adjazenzmatrix handelt, da die Supraadjazenzmatrix unterschiedliche Kanten speichert, und einen positiven Eintrag in den Diagonalblöcken nicht äquivalent zu einen positiven Eintrag in nicht Diagonalblöcken ist.

Im Folgenden werden wir in der Wissenschaft häufig genutzte Netzwerke vorstellen, die sich durch eine Multilayer Struktur gut repräsentieren lassen und zeigen wie ihre Supraadjazenzmatrix aussieht.

3.2.1 Muliplex-Netzwerke

Bei klassischen Netzwerken sind die Verbindungen binär: Entweder sind zwei Knoten miteinander verbunden oder nicht. Bei komplexeren Strukturen können Netzwerke erweitert werden, um mehr Information zu enthalten. Es ist beispielsweise möglich, jeder Kante ein Gewicht zuzuordnen. Dieses kann den Abstand zwischen zwei Bushaltestellen repräsentieren oder wie viele Stunden sich zwei Menschen sich in einer Woche sehen. Man kann auch verschiedene Art von Verbindungen darstellen. Zum Beispiel können zwei Menschen als Freunde oder als Mitarbeiter verbunden sein. Es ist möglich jede unterschiedliche Verbindungsart mit einer unterschiedlichen Farbe darzustellen. Multilayer-Netzwerke stellen eine andere Repräsentationsmöglichkeit für solche Netzwerke da. Es ist möglich, für einen Graphen M und jede Verbindungsart \(α\) einen Layer \(α’\) festzulegen. Dabei stehen in Layer \(α’\) alle Knoten und genau die Kanten, welche den Typ \(α\) haben (Bianconi, 2018). Internationale Beziehungen lassen sich von solchen multiplex Netzwerke repräsentieren. Stellen wir uns beispielsweise vor, dass Amerika mit Israel und Großbritannien ein militärisches Bündnis unterhält. Russland, China und Iran stellen wiederum ein eigenes Bündnis dar. Außerdem findet Handel zwischen allen besagten Ländern mit China, Amerika und Großbritannien, Russland und Israel sowie auch Russland und Iran statt. Die folgenden internationalen Beziehungen lassen sich durch ein gefärbtes Graph darstellen.

Multi-Color Netzwerk (Bianconi, 2018)

Die roten Kanten bezeichnen militärische Alliierte und die grünen Kanten wirtschaftliche Beziehungen. Als Multiplex Netzwerk lässt sich folgender Graph durch die schon erwähnte Methode darstellen.

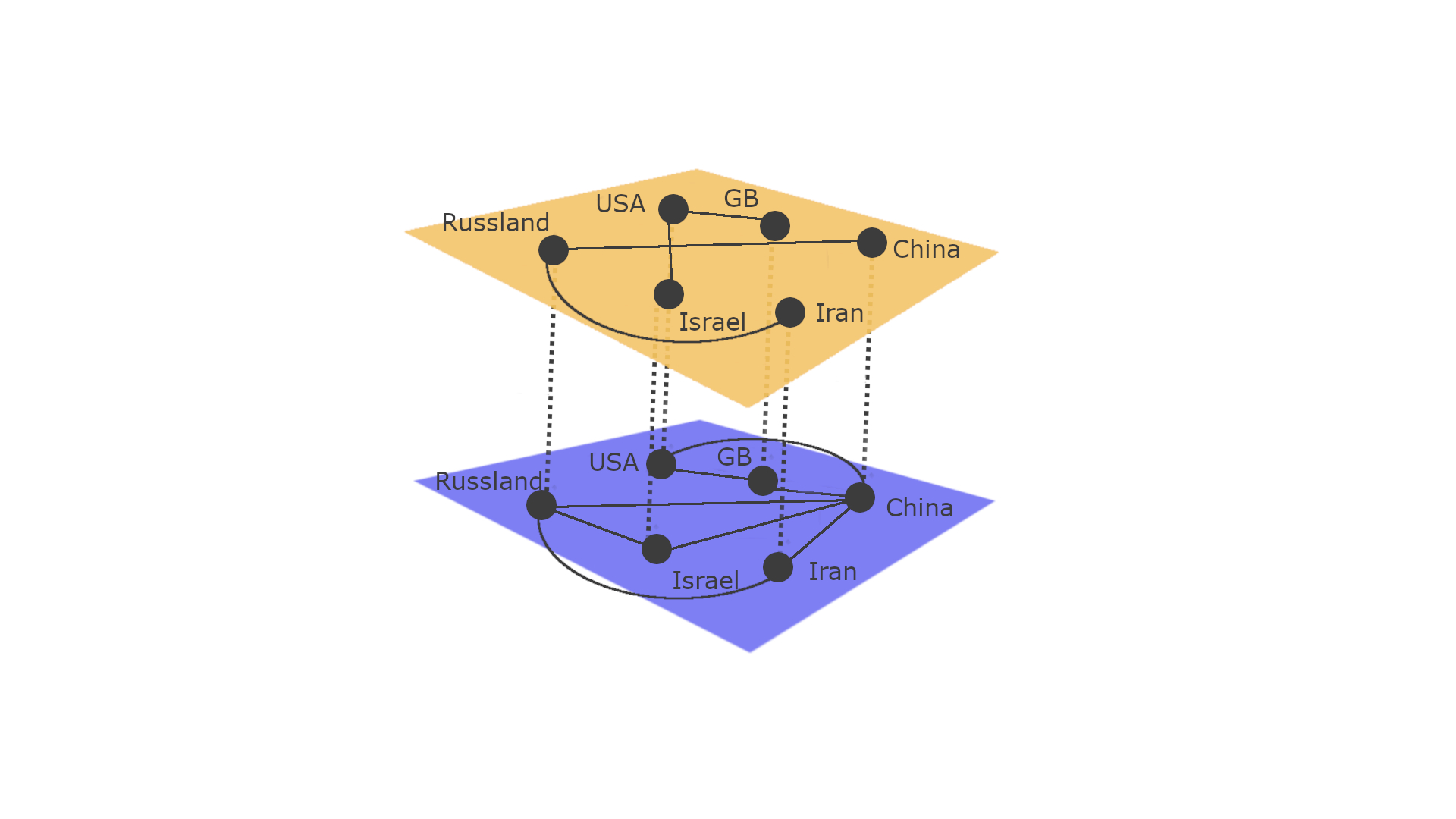
Ungewichtetes und ungerichtetes Multiplex Netzwerk

Image of airlines, Multilayer-Netzerk. Jede Ebene repräsentiert eine unterschiedliche airline (Porter, 2018)

In solchen Multiplex Netzwerke können nur zwei Knoten aus unterschiedlichen Kanten verbunden sein, wenn sie identisch sind (replica nodes) (Bianconi, 2018). Solche Verbindungen sollen zur Identifizierung für interlayer communities helfen. Wenn beispielsweise ein Land aus ökonomischen Gründen mit der USA verbunden ist und die USA eine militärische Allianz mit Israel unterhält, so ist dieses Land auch mit Israel verbunden.

Klassische Graphen mit n Knoten lassen sich durch eine Adjazenzmatrix A aus ℝ (nxn) darstellen, wobei

\[A_{ij}=\begin{cases} 0,\text{wenn es keine Kante von Knoten i nach Knoten j gibt.}\\ 1,\text{sonst.} \\ \end{cases}\]

Für Multiplex Netzwerke kann man jede Ebene als einen solchen Graphen betrachten. So ist für jeden Layer \(α\) die Adjazenzmatrix \(A[α]\) als die Adjazenzmatrix von Layer \(α\) definiert. Genau: \(A_{ij}^{[α]}=\begin{cases} 0, \text{wenn es keine Kante von Knoten i nach Knoten j in Layer α gibt,} \\ 1, \text{sonst}\\ \end{cases}\)

Um den ganzen Graphen zu repräsentieren, wird die Supraadjazenzmatrix benutzt (Bianconi, 2018). Die Supraadjazenzmatrix besagt: Für einen Knoten \(i\) aus Layer \(α\) und \(j\) aus \(β\), ob eine Kante zwischen diesen Knoten gibt. Genauer gesagt:

\[A_{ij}^{[α,β]}=\begin{cases} 0, \text{falls es keine Kante zwischen Knoten i im Layer αm und Knoten j in Layer β gibt},\\ 1, sonst\\ \end{cases}\]

Wir wissen, falls \(α= β\) (falls beide Knoten sich im selben Layer befinden) wird diese Zahl von der Adjazenzmatrix \(A_{ij}^{[α]}\) gegeben. Ansonsten (wenn die Knoten sich in unterschiedlichen Layers befindet), sind \(i\) und \(j\) genau dann verbunden, wenn \(i = j\).

Die Adjazenzmatrix hat also die Form:

\(A = \begin{pmatrix} a^{[1,1]} & | & I & | & ... & | & I\\ ---- & & ---- & & ---- & & ---- \\ I & | & a^{[2,2]} & | & ... & | & I \\ ---- & & ---- & & ---- & & ---- \\ ... & | & ... & | & ... & | & .... \\ ---- & & ---- & & ---- & & ---- \\ I & | & I & | & ... & | & a^{[M,M]} \\ \end{pmatrix}\) (Bianconi, 2018)

Wobei I die Identitätsmatrix ist. Die Funktion \(δ(i, j)\) (bekannt als Kroenecker delta) liefert 1 zurück, falls \(i\)=\(j\) ist, sonst 0. Also kann man allgemein sagen

\(A_{ij}^{[α,β]}= \begin{cases} A_{ij}^{[α]}, \text{wenn α = β}\\ δ(i, j), sonst\\ \end{cases}\) (Bianconi, 2018)

Zur Vereinfachung kann man das “Agreggated” Netzwerk bilden. Diese kann man sich als die Vereinigung aller Layers vorstellen. Sei G ein Multislice Graph mit Knoten \(V = {v_1,…,v_n}\) und Ebenen {\(α_1\),…,\(α_n\)} Zwei Knoten \(v_{i}\) und \(v_j\) sind im “Aggregated Netzwerk” \(v_n\) G genau dann verbunden, wenn sie mindestens in einen Layer von G verbunden sind. (Bianconi, 2018) Man verliert selbstverständlich Information, da man im “Aggregated Netzwerk” nicht weißt, an welchem Zeitpunkt zwei Knoten verbunden waren, aber die Vereinfachung kann die Laufzeit von Algorithmen verbessern, die Visualisierung deutlicher machen, sowie andere Probleme wie “the damn of dimensionality” verhindern. Unter diesen Begriff, geprägt von Richard Bellman, versteht man das Wachstum an Komplexität und Schwierigkeit in unterschiedliche Probleme, wenn die Anzahl der Variablen (bzw. Dimensionen) erhöht wird (Kuo & Sloan, 2005).

3.2.2 Multislice Netzwerke

Bei Pandemien ist es natürlich Hilfreich, nicht ein Netzwerk allein zu einem bestimmten Zeitpunkt zu betrachten, sondern auch die Evolution entlang der Zeit. Da es zwischen zwei Zeitpunkten \(a\) und \(b\) mit \(a\neq b\) unendlich viele Zeitpunkte gibt, kann man nicht das Netzwerk für alle Zeitpunkten betrachten. Stattdessen teilt man die Zeit in Perioden der Längen \(δ\), und ordnet jeder Zeitperiode x einem Netzwerk zu, welches genau die Verbindungen im Zeitpunkt x repräsentiert (Bianconi, 2018). Verbindungen zwischen Layers (interlinks) gibt es nur zwischen nacheinander folgenden identischen Knoten. Das heißt, es gibt eine Kante von Knote \(i\) aus \(α\) zu \(j\) aus \(β\) genau dann, wenn Layer \(β\) den Zeitpunkt nach \(α\) repräsentiert und \(i = j\). Zur Repräsentation wird das Triplet \(M = (Y, G , G)\) benutzt. Wobei Y die Menge der Ebenen ist \(G_α\) für jedes \(α\) die Menge (\(V_α\), \(E_α\)) repräsentiert (die Knoten und Kanten der Ebene \(α\)) und die Netzwerke \(G\) nur Verbindungen zwischen zwei nacheinander folgenden Ebene enthalten.

Aufgrund der Einschränkung für “interlinks” besitzt die Adjazenzmatrix eines solchen Netzwerks die Form:

\(A = \begin{pmatrix} a^{[1,1]} & | & I & | & ... & | & 0\\ ---- & & ---- & & ---- & & ---- \\ 0 & | & a^{[2,2]} & | & ... & | & 0 \\ ---- & & ---- & & ---- & & ---- \\ ... & | & ... & | & ... & | & .... \\ ---- & & ---- & & ---- & & ---- \\ 0 & | & 0 & | & ... & | & a^{[M,M]} \\ \end{pmatrix}\) (Bianconi, 2018)

3.2.3 Implementierungen aus der klassischen Netzwerke

Viele Algorithmen für klassische Netzwerke welche mit der Adjazenzmatrix arbeiten, lassen sich auch für Supraadjazenzmatrizen implementieren. Als Beispiel können wir uns das folgende Problem vorstellen. Wir haben einen klassischen Graph \(G\) und eine Adjazenzmatrix \(A\). Man möchte wissen, was der kürzeste Pfad zwischen von Knoten \(i\) nach Knoten \(j\) ist. Erinnerung: Laut der Regeln der Matrixmultiplikation

\(A^{2}_{ij}\) := \(\sum_{i=1}^{n} A_{ik}*A_{kj}\)

Das Produkt \(a_{ik}\)* \(a_{kj}\) ist genau dann 1, wenn beide Multiplikanden 1 sind (wenn \(a_{ik}\)=1 und \(a_{kj}\)=1 sind). In anderen Worten, wenn es eine Kante von \(i\) nach \(k\) und \(k\) nach \(j\) gibt. Die Summe ergibt also die Anzahl aller Pfade der Länge 2 von \(i\) nach \(j\).

Im Allgemein gilt, wenn man im \(A\) hoch n nimmt, hat man im ijten Eintrag die Anzahl von Wege der Länge n von \(i\) nach \(j\). Ein möglicher Algorithmus, um den kürzesten Pfad von Knoten \(i\) nach Knoten \(j\) zu finden, ist die Matrix \(A\) mit sich selbst multiplizieren, bis es im \(ij_{ten}\) Eintrag keine 0 gibt (bis es mindestens einen Pfad gibt). Die Potenz der Matrix entspricht also die Länge des kürzesten Pfades (Duncan, 2004).

3.3 Vergleich

Betrachtet man die drei vorgestellten Möglichkeiten zur Darstellung von allgemeinen Multilayer-Netzwerken fällt auf, dass das Modell von Kivela M.(Kivela et al., 2014) im Gegenteil zum Modell, welche von Ginestra Bianconi vorgeschlagen wurde (Bianconi, 2018) und die Supraadjazenzmatrix, die Möglichkeit bietet Ebenen in Aspekte zu gruppieren. Ein Aspekt besteht aus mehreren Ebenen und dient dazu die Ebenen zu kategorisieren. Zur Analyse von Multilayer Netzwerken ist dies hilfreich, da man so nicht nur Zusammenhänge zwischen einzelnen Ebenen, sondern auch zwischen Aspekten herstellen kann. Als Beispiel sei ein Multilayer Netzwerk gegeben, dass für jedes Jahr die meiste genutzte Sozialmedia Plattform einer Person darstellt (Kivela et al., 2014). Nun kann man die Zeit und Sozialmedia-Plattformen als Aspekte \(L_1,L_2L_1,L_2\) interpretieren und die tatsächlichen Einträge als Ebenen: \(L_1=2020,2021,L_2=Facebook,Instagram L_1=2020,2021,L_2=Facebook,Instagram\). Die Ebenen sind jetzt klar strukturiert und es kann einfach nachvollzogen werden, welche Kanten innerhalb eines Aspekts verlaufen und welche die Aspekte verbindet. Diese Funktion der Aspekte ist im Repräsentationsmodell von Ginestra Bianconi (Bianconi, 2018) und bei der Supraadjazenzmatrix nicht gegeben, kann aber einfach simuliert werden. Durch das Hinzufügen weiterer Ebenen und Knoten kann die Zugehörigkeit einer Ebene zu einem Aspekt simuliert werden. Dazu kann für jedes Aspekts ein neuer Knoten zu jedem Graphen aus der Liste \((\vec{G})\) hinzugefügt werden. Diese Knoten werden zu den jeweiligen Aspekten mit Interlinks zu einer neuen Ebene verbunden. Jedoch ist es anschaulicher mit dem Modell von Kivela M. (Kivela et al., 2014) zu arbeiten, wenn man Aspekte verwenden will. Die Besonderheit in der Definition aus von Ginestra Bianconi(Bianconi, 2018) , sowohl als auch für die Supraadjazenzmatrix ist, dass hier die Struktur der einzelnen Ebenen klar erkennbar ist. Es gibt nicht eine große Knoten- und Kantenmenge, sondern für jede Ebene einen alleinstehenden Graphen wie auch für jedes Ebenenpaar einen Interlink Graphen. Für die Supraadjazenzmatrix kann man den Blöcken als Adjazenzmatrix für jede Ebenegraph bzw. als Interlink Graph für jedes Ebenenpaar betrachten. Dies könnte von Vorteil sein, wenn die Ebene auch unabhängig vom Multilayer-Netzwerk untersucht werden sollen, da hier jede Ebene unabhängig voneinander definiert wurde. Nehmen wir als Beispiel ein Multilayer-Netzwerk, welches für jeden Nutzer eine Ebene anlegt und die Knoten auf der Ebene die geliketen Beiträgen auf einer Socialmedia-Plattform darstellen. Ein Interlink wird hinzugefügt, wenn der Beitrag der gleiche ist. Falls man nun auch Eigenschaften für jeden Nutzer, zum Beispiel, ob eine Mindestzahl von Beiträgen geliket wurde, überprüfen will fällt dies leichter. Jedoch ist bei dieser Methode der Verwaltungsaufwand größer, da jeder Graph einzeln angelegt wird. Die Supraadjazenzmatrix hat insbesondere den Vorteil, dass man viele Algorithmen der Graphentheorie, die für Adjazenzmatrizen geeignet sind, sowie die Suche nach dem kürzesten Pfad zwischen zwei beliebigen Knoten, sich auf die Supraadjazenzmatrix implementieren lassen.

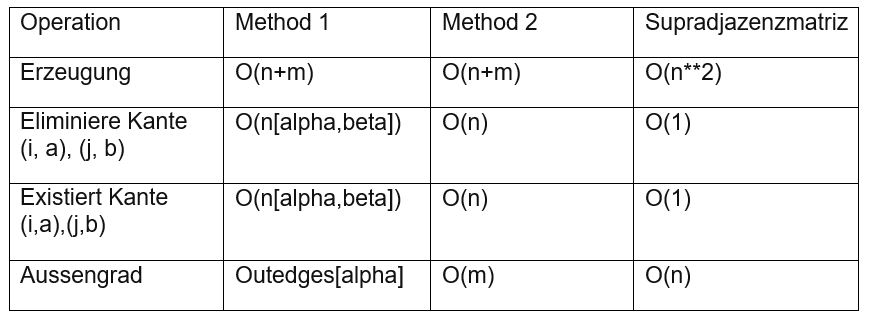
Ein anderer Aspekt, den man betrachten sollte, ist der Zeitaufwand für unterschiedliche Operationen, sowie Kanten löschen oder hinzufügen. Dafür haben wir uns den Zeitverbrauch für die jeweiligen Repräsentationsmöglichkeiten überlegt.

Eine häufige Operation wäre eine Kante auf Existenz zu untersuchen. Man möchtet also herausfinden, ob ein Knoten \(i\) aus Ebene \(α\) mit einem Knoten \(j\) aus Ebene \(β\) verbunden ist. Für eine Adjazenzmatrix muss man einfach den Eintrag von \(A_{ij}^{[α, β]}\) lesen. Falls dieser 1 ist, so existiert die Kante, andernfalls nicht. Da diese Operation nicht von der Größe der Matrix abhängt, lässt sie sich in konstanter Zeit berechnen. In der Informatik bezeichnet man solche Algorithmen mit der Notation \(O(1)\).

Wenn man Modell 1 als Datenstruktur implementiert, muss man die Liste \(E_{[α, β]}\) durchlaufen (die Liste mit dem Kanten von Ebene \(α\) nach Ebene \(β\)). Falls die Kante gefunden wurde, so existiert sie tatsächlich. Andernfalls befindet sich die Kante nicht im Graph. Der Zeitaufwand ist also linear abhängig zur Größe von \(E_{[α,β]}\), und hat somit die Zeitkomplexität \(O(|E_{[α,β]}|)\).

Bei dem zweiten Modell muss man die ganze Liste EM durchlaufen, bis man \(((i,α),(j,β))\) findet. Falls das Element sich in der Liste befindet, so existiert tatsächlich die Kante, andernfalls nicht. Die Laufzeit ist also proportional zur Anzahl der Kanten im Graphen und hat somit die Zeitkomplexität \(O(|E_{m}|)\).

Bei Eliminieren einer Kante geht es analog. Man muss die Kante zuerst suchen. Dabei hat man \(O(1)\) Komplexität für die Supraadjazenzmatrix, \(O(|E_{[α, β]}|)\) für Methode 1 und \(O(|E_{m}|)\) für Methode 2. Dann muss man die Kante eliminieren.Dies lässt sich in konstanter Zeit für alle Strukturen lösen. Somit ist die Zeitkomplexität der Operation löschen für alle Datenstrukturen identisch zur Zeitkomplexität der Operation „finden“.

Bei der Berechnung des Außen-Grads eines Knotens \(i\) im Layer \(α\) (die Menge von Kanten, die aus diesem Knoten gehen), muss man in der Supraadjazenzmatrix einfach die \(A_{[α]}^{[i]}\) zugehörige Zeile durchgehen und dabei alle Einträgen summieren. Da diese Zeile genau so groß wie die Menge der Knoten ist, ergibt sich einen Zeitaufwand von \(O(n)\). Wobei n die Menge der Knoten ist. Identische Knoten aus unterschiedlichen Ebenen werden als unterschiedliche Knoten betrachtet.

Bei Modell 1 muss man alle Listen von Kanten untersuchen, die Kanten aus Layer \(α\) enthalten und dabei alle Zählen, die von Konten \(i\) ausgehen. Insgesamt also ist der Zeitaufwand proportional zur Anzahl der Kanten, die aus Layer \(α\) gehen. \(O(Außengrad(α))\), wobei Außengrad(\(α\)) die Menge der Kanten ist, die aus Layer \(α\) gehen.

Bei Modell 2 muss man die Listen der Kanten durchgehen, und die Anzahl von Kanten zählen, die mit (\(α\), \(i\)) anfangen. Der Zeitaufwand ist also proportional zur Länge der Kanten \((O(|V_m|))\). Bei der Erzeugung des Graphen, hat jedoch die Supraadjazenzmatrix den Nachteil, dass man zwischen zwei beliebigen Knoten einen Eintrag hat. Dieser ist 1, falls es eine Kante zwischen den Knoten gibt, und andernfalls 0. Der Zeitaufwand für die Erzeugung einer Supraadjazenzmatrix ist also \(O(n^2)\), wobei n die Anzahl der Knoten ist. Wobei auch hier wieder gilt, identische Knoten in unterschiedliche Layers werden als unterschiedliche Knoten betrachtet. Bei Modell 1 und 2 muss man die Knoten und Kanten speichern, und deswegen haben sie bei der Erzeugung einen Aufwand von \(O(n+m)\).

Laufzeiten der Operationen für jedes Modell

4. Zusammenfassung

In unserer Arbeit haben wir eine Übersicht verschiedener Möglichkeiten, Multilayer-Netzwerke mathematisch zu repräsentieren, dargestellt. Dazu haben wir drei Definitionen vorgestellt und verglichen, welche Art von Mutilayer-Netzwerk für welchen Anwendungsfall geeignet ist. Das erste Modell stellt jede Ebene als einzelnen Graphen dar und bietet somit die Möglichkeit die Ebenen auch unabhängig voneinander zu betrachten. Das zweite Modell führt eine Definition ein, um Ebenen bestimmen Aspekten zuzuordnen. Die dritte Möglichkeit stellt jede Ebene als Graphen dar und speichert die Information in einer Matrix. Außerdem erläuterten wir Spezialfälle von Multilayer-Netzwerken, welche in der Wissenschaft häufig vorkommen, wie Multiplex und Multislice.

Insgesamt wurde gezeigt, dass keine Modell für alle Anwendungen am besten geeignet ist. Jede Darstellungsmöglichkeit hat seine Vor- und Nachteile. Das Modell 2 erlaubt, die Ebenen in unterschiedliche Aspekte zu klassifizieren und ist somit Informationsreicher. Allerdings sind Modell 1 und die Supraadjazenzmatrix besser zur Visualisierung geeignet, da man jede Ebene selbständig betrachten kann. Desweiteren hat die Supraadjazenzmatrix bei den meisten Operationen, die man auf einen Multilayer-Netzwerk machen möchtet, eine geringere Laufzeit. Das ist jedoch nicht der Fall bei Graphen mit weniger Kanten im Vergleich zur Knotenmenge. Somit können wir schlussfolgern, dass die Supraadjazenzmatrix in den meisten Fällen, eine bessere Darstellungsmöglichkeit ist, obwohl für bestimmte Anwendungen andere Repräsentationsmöglichkeiten von Vorteil sein können. Dieser Beitrag kann genutzt werden, um die Wahl eines Repräsentationsmodells in zukünftigen wissenschaftlichen Arbeiten zu erleichtern.

5. Referencen

  1. Kivela, M., Arenas, A., Barthelemy, M., Gleeson, J. P., Moreno, Y., & Porter, M. A. (2014). Multilayer networks. Journal of Complex Networks, 2(3), 203–271. https://doi.org/10.1093/comnet/cnu016
  2. Bianconi, G. (2018). Multilayer networks: Structure and function (First edition). Oxford University Press.
  3. Boccaletti, S., Bianconi, G., Criado, R., del Genio, C. I., Gómez-Gardeñes, J., Romance, M., Sendiña-Nadal, I., Wang, Z., & Zanin, M. (2014). The structure and dynamics of multilayer networks. Physics Reports, 544(1), 1–122. https://doi.org/10.1016/j.physrep.2014.07.001
  4. Porter, M. A. (2018). What Is... a Multilayer Network? Notices of the American Mathematical Society, 65(11), 1. https://doi.org/10.1090/noti1746
  5. Marcello Tomasini. (2015). An Introduction to Multilayer Networks. 3966. https://doi.org/10.13140/RG.2.2.16830.18243
  6. Kuo, F. Y., & Sloan, I. H. (2005). Lifting the curse of dimensionality. Notices of the AMS, 52(11), 1320–1328.
  7. Duncan, A. (2004). Powers of the adjacency matrix and the walk matrix.