Deep Learning
| Florian Plümäkers | Johannes Ehls |
|---|---|
| RWTH Aachen | RWTH Aachen |
| florian.pluemaekers@rwth-aachen.de | johannes.ehls@rwth-aachen.de |
Die Bedeutung von Netzwerken sowohl im Kontext der steigenden Popularität von sozialen Netzwerken als auch im Kontext der Bio-Informatik nimmt immer weiter zu. Von besonderer Bedeutung ist dabei die Identifizierung von einander überlappenden Gruppierungen, welche in sozialen Netzen zum Beispiel für Empfehlungssysteme auf Basis von Gemeinsamkeiten in solchen Gruppen oder in der Bio-Informatik zur Analyse von Molekülen verwendet werden. In diesem Kapitel des Online-Buches fokussieren wir uns auf die Gruppenidentifizierung mit Hilfe von Deep Learning-Algorithmen, also einem Ansatz des maschinellen Lernens. Dazu unterscheiden wir in unserer Arbeit verschiedene Graph-Neural-Network-Algorithmen (GNN), vergleichen ihre Ansätze untereinander, stellen Gemeinsamkeiten und Unterschiede heraus. Anschließend lassen wir die Implementierung eines Line Graph Neural Network (LGNN) auf Datensätzen laufen und analysieren daraufhin verschiedene Kriterien. Abschließend visualisieren wir die Resultate. Ziel der Arbeit ist es also, Deep Learning Algorithmen zur Community Detection und im Speziellen das LGNN Modell zu verstehen und anhand des Experimentes Vor- und Nachteile herauszustellen.
Inhaltsverzeichnis
1. Einleitung
2. Verwandte Arbeiten
3. Methodik
3.1 Kernidee Linear Graph Neural Network (LGNN)
3.2 LGNN Layer/Struktur des Algorithmus
3.3 Verlustfunktion/Loss Function
4. Anwendung
4.1 Bewertung
4.2 Visualisierung der gefundenen Communities
5. Zusammenfassung/Ausblick
6. Referenzen
1. Einleitung
Im Internet ist man alltäglich umgeben von personaliesierten Inhalten, wie z.B. aktuellen Neuigkeiten, neuen Kontaktvorschlägen oder zu den Interessen passende Werbung. Da die meisten Menschen Kontakt zu mehreren Menschen haben und verschiedene Interessen teilen, braucht man Algorithmen, welche überlappenden Communities erkennen können, wie z.B Familie, Freunde oder Kunden. Das Ziel dieser Algorithmen ist es jede Person mindestens einer Community zuzurodnen. Aktuell werden meist Algorithmen verwendet, welche einen Knoten nur einem Graphen zuordnen, da aber jeder Mensch teil verschiedener Communities sein kann, gilt es diese überlappenden Gruppierungen zu identifizieren. Des Weiteren gehen wir dem Streben nach höherer Effizienz und besserer Laufzeit nach. Um dies zu erreichen verfolgen wir hier den Ansatz des Deep Learnings, welcher das Lernverhalten des Menschen mittels großer Datenmengen nachahmt. Allgemein gibt es beim Deep Learning drei Bereiche, die Eingabeschicht, welche beispielsweise einen HTML Farbcode für einen Pixel bekommt, die verborgenen Schichten, in denen die Informationen verarbeitet und reduziert werden und es gibt die Ausgabeschicht, welche schließlich zum Ergebnis führt. Es gibt eine Vielzahl an Deep Learning Algorithmen, wie wir bei den verwandten Arbeiten auch weiter drauf eingehen werden, in diesem Kapitel werden wir uns aber auf einen LGNN (Linear Graph Neural Networks) Algorithmus beschränken. Deep Learning wird in sehr vielen komplexen Bereichen erfolgreich eingesetzt, beispielsweise beim autonomen Fahren, in der Medizin oder bei der Spracherkennung. Deshalb bietet Deep Learning ein großes Potential für die die Erkennung von überlappenden Communities. Im Folgenden fangen wir an verwandte Arbeiten zu Deep Learning zu zeigen, da wir auf der Arbeit “Line graph neural network” von Qi Huang, Yu Gai, Minjie Wang und Zheng Zhang aufbauen. Im Anschluss dazu, werden wir genauer auf die Methodik hinter dem LGNN Algorithmus eingehen.
2. Verwandte Arbeiten
Wie eben erwähnt, gibt es viele verschiedene Deep Learning Algorithmen für die Identifizierung überlappender Communities. Ein bekannter Algorithmus ist beispielsweise der Autoencoder. Hierbei gibt es einen Codierer und einen Decodierer. Der Codierer bekommt einen Datenpunkt und wandelt diesen in einen niedriger dimensionale Darstellung (Embedding) um. Anschließend nimmt der Decodierer das Embedding und rekonstruiert die ursprüngliche Eingabe. Diese Rekonstruktion ist die Ausgabe des Autoencoders. Die Verlustsfunktion des Autoencoders misst den Informationsverlust zwischen der Rekonstruktion (Tran, 2018).
Des Weiteren gibt es den VAE (Variational Autoencoder), eine Abwandlung des Autoencoders. Die Grundidee hiervon ist, dass der Codierer die Eingabe in eine Verteilung codiert, statt in einen Punkt. Danach wird ein zufälliges Element aus dieser Verteilung. Die Verlustfunktion besteht aus zwei Teilen. Der erste Teil misst, wie gut das Netzwerk die Daten rekonstruiert hat. Der zweite Teil misst, wie ähnlich die Ausgangsverteilung der Anfangsverteilung ist (Khan & Kleinsteuber, 2020).
Es gibt jedoch noch viele weitere Deep Learning Algorithmen für die Graphen Analyse bzgl. Community Dectection, z.B. DFF (Deep Feed Forward), DCN (Deep Convolutional Network), RNN (Recurrent Neural Network) oder NTM (Neural Turing Machine). Unser verwendeter Algorithmus baut auf dem LGNN Algorithmus von Qi Huang, Yu Gai, Minjie Wang und Zheng Zhang auf (Han, 2019).
3. Methodik
Ziel ist es, wie bei anderen OCD-Graphenalgorithmen auch, sich überlappende Communities zu finden, das heißt zu jedem Knoten eines gegebenen Graphen ein Label zu finden, sodass Knoten mit dem gleichen Label einer Community angehören. Entsprechend formulieren wir auch beim LGNN Algorithmus (Line Graph Neural Network - Algorithmus):
Input: \(G = (V,E)\)
Output: \(y:V \mapsto \{1, C\}\),
wobei \(G\) ein Graph mit Knoten \(V\) und Kanten \(E\) ist und \(y\) genau die Funktion, die jedem Knoten \(V\) eine Gruppe bzw. Community zuordnet. \(V\) wird also in \(C\) Gruppen partitioniert (Chen et al., 2018).
Da der LGNN-Algortihmus ein Deep-Learning Algorithmus ist, muss dieser “trainiert” werden. Dazu verwenden wir Trainigsdatensätze, welche aus Tupeln von je einem Graphen und einer zugehörigen Funktion, welche jedem Knoten ein Label zuordnet (also dem späteren Output). Trainiert wird, indem der Algortihmus seine eigenen Labels berechnet und diese dann mit denen aus dem Trainingsdatensatz verglichen werden, dies passiert mit einer speziellen “Loss-Funktion”. Je größer die entsprechenden “Losses” sind, desto mehr wird sich das Model bzw. der Algorithmus in der nächsten Iteration des Trainings verändern. Wenn das Model ausreichend trainiert ist, kann es auf beliebigen Graphen Communities, also entsprechende Labels bestimmen.
Ziel ist es also, das Model
\[\hat{y}=\Phi(G,\theta)\]mit gegebenen Testdaten \(\{(G_t,y_t)\}_{t\leq T}\) zu Trainieren, wobei es das Ziel ist, die Loss-Funktion $$ L(\theta)=\frac{1}{T}\sum_{t\leq T}l(\Phi(G_t,\theta),y_t) $$ zu minimieren. Hierbei bezeichnet \(T\) die Gesamtzahl der Tupel aus Graphen und Labels (Chen et al., 2018). Es wird also der Mittelwert der Losses über den Trainingsdatensatz ermittelt. Wie genau die einzelnen Losses \(l\) ermittelt werden, darauf gehen wir später im Kapitel 3.3 ein. Außerdem finden Sie eine Erklärung dazu im ersten Video.
Video 1: Setup Methodik und Loss-Funktion
Wir benötigen neben der Loss-Funktion für unser Modell außerdem ein GNN also ein Graph Neural Network und zusätzlich ein LGNN (Kap. 3.1). Dabei ist das GNN ziemlich ähnlich zum Inputgraph \(G\) und wird aus diesem erstellt. Auch das LGNN wird aus dem Inputgraphen \(G\) berechnet, dies ist jedoch etwas komplexer. Wie genau das passiert, beschreiben wir im Folgenden.
3.1 Kernidee Linear Graph Neural Network (LGNN)
In der Graphentheorie repräsentiert der sogenannte Line Graph die Kanten-Adjazenz-Strucktur aus dem zugrundeliegenden Graph. Insbesondere verwandelt der Line Graph \(L(G)=(V_L,E_L)\) eine Kante im originalen Graph G in einen Knoten. Sind also zwei Kanten \(e_A:=(i \to j)\) und \(e_B:=(j \to k)\) mit \(i,j,k \in V\) aus dem Graphen \(G\), dann existieren im Line Graph \(L(G)\) die korrespondierenden Knoten \(v_A^l\) und \(v_B^l\). Falls \(G\) ein ungerichteter Graph ist, dann existiert je ein Knoten für Hin- und Rückrichtung, also ergibt sich \(\vert V_L \vert = 2 \vert E \vert\) (Chen et al., 2018).
Die Knoten in \(L(G)\) werden folgendermaßen verbunden. Zwei Knoten sind verbunden, falls gilt
\[\begin{align*} B_{(i\to j),(i'\to j')}=\left\{\begin{array}{rcl}1 &,& \text{wenn }j=i'\text{ und }j'\neq i,\\0 &,& \text{sonst.}\end{array}\right. \end{align*}\]Diese mathematische Definition sagt aus, dass zwei Knoten \(v_A^l\) und \(v_B^l\) in \(L(G)\) dann und nur dann verbunden werden, wenn sich die korrespondierenden Kanten \(e_A\) und \(e_B\) in \(G\) einen Knoten teilen, nämlich den Zielknoten von \(e_A\) und den Startknoten von \(e_B\).
Erklärung der Kernidee von LGNNs im Video
3.2 LGNN Layer/Struktur des Algorithmus
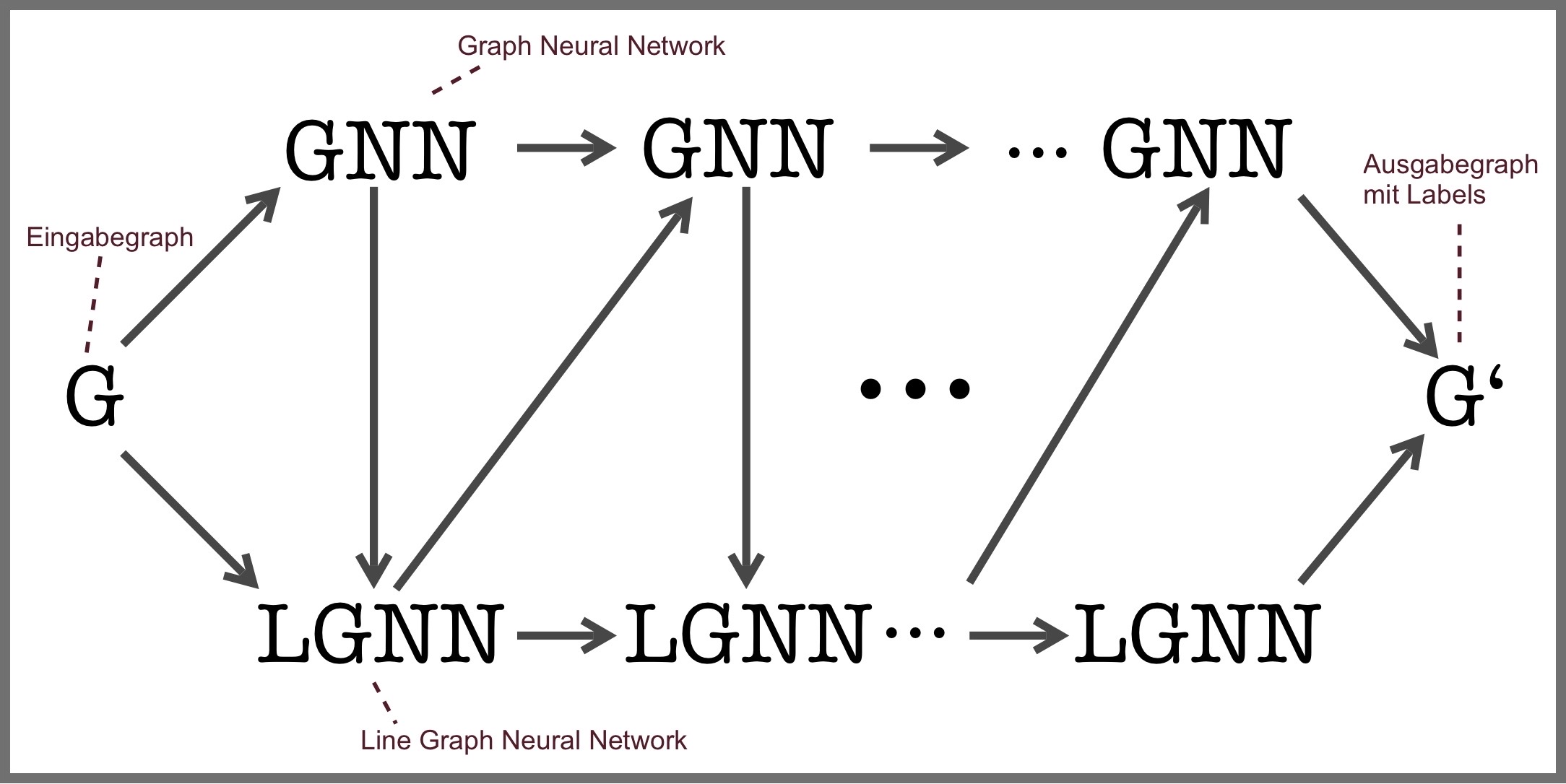
Das Modell beziehungsweise der Algorithmus setzt sich aus mehreren Schichten von je einem GNN und einem LGNN zusammen. Oben haben wir bereits gezeigt wie ein LGNN aus dem Inputgraphen erstellt wird. Jetzt betrachten wir beispielhaft, wie sich die \(k\)-te Layer, das \(i\)-te Neuron (Knoten) und der \(l\)-te Channel während eines Traininsschritts (Epoche) aktualisiert. Der Datenfluss lässt sich wie folgt abstrahieren:
Abbildung 1: Mehrere Schichten (Layers) des Modells bestehend aus GNNs und LGNNs
Wie man leicht erkennen kann, dient der Output des \(k\)-ten GNN als Input für das \(k\)-te LGNN, während dessen Output einen Input für das \((k+1)\)-te GNN darstellt. Genauer kann man diesen Informationsfluss anhand folgender Gleichungen nachvollziehen. Dabei gehört \(x^{(k+1)}_{i,l}\) zum entsprechenden GNN und \(y^{(k+1)}_{i',l'}\) ist das symmetrische Äquivalent welches zum LGNN gehört.
\(x^{(k+1)}_{i,l} = \rho \left[ x_i^{(k)}\theta_{1,l}^{(k)} + (Dx^{(k)})_i\theta^{(k)}_{2,l} + \sum_{j=0}^{J-1}(A^{2^j}x^{(k)})_i\theta^{(k)}_{3+j,l} + \{Pm,Pd\}y^{(k)}\theta^{(k)}_{3+J,l} \right] , i \in V\)
\(y^{(k+1)}_{i',l'} = \rho \left[ y_{i'}^{(k)}\gamma_{1,l'}^{(k)} + (D_{L(G)}y^{(k)})_{i'}\gamma^{(k)}_{2,l'} + \sum_{j=0}^{J-1}(A^{2^j}_{L(G)}y^{(k)})_{i'}\gamma^{(k)}_{3+j,l'} + [\{Pm,Pd\}^{\top}x^{(k+1)}]_{i'}\gamma^{(k)}_{3+J,l'} \right] , i' \in V_L\)
Die Gleichungen bestehen im wesentlichen aus vier Summanden (wir nutzen die erste Gleichung als Beispiel). Jeder Summand enthält \(\theta\), einen Trainingsparameter:
- \(x_i^{(k)}\theta_{1,l}^{(k)}\), eine lineare Projektion des Outputs \(x^{(k)}\) der vorherigen Layer multipliziet mit Trainingsparameter \(\theta\)
- \((Dx^{(k)})_i\theta^{(k)}_{2,l}\), eine lineare Projektion des sogenannten Degreeoperators auf \(x^{(k)}\), multipliziert mit Trainingsparameter \(\theta\); der Degreeoperator \(D\) multipliziert den Knotengrad \(deg(i)\) mit \(x_i\)
- \(\sum_{j=0}^{J-1}(A^{2^j}x^{(k)})_i\theta^{(k)}_{3+j,l}\), eine Summe über die Adjazenzmatrix \(A\) hoch \(2^j\) multipliziert mit \(x^{(k)}\) und Trainingsparameter \(\theta\)
- \(\{Pm,Pd\}y^{(k)}\theta^{(k)}_{3+J,l}\), vereinigen mit dem Output des jeweils anderen Graphen (wie oben beschrieben), hier als Multiplikation von \(\{Pm,Pd\}\) mit \(y^{(k)}\)
Hierzu ist noch anzumerken, dass hier \(\{Pm,Pd\}\) als Adjazenzmatrix des Bipartiten Graphen aufgefasst werden kann, der die Features (Knoten) des LGNN auf die des GNNN abbildet und anders herum. Daher ist die Matrix hier von Dimension \(Pm, Pd \in \{0,1\}^{|V| \times 2|E|}\) (Chen et al., 2018).
Weitere Informationen zum LGNN befinden sich in Video 2 (unten).
Video 2: LGNN Aufbau/Kernidee und Struktur eines Layers
3.3 Verlustfunktion/Loss Function
Wie oben bereits erwähnt, ist es das Ziel des Modells, die Loss-Funktion \(L(\theta)\) zu minimieren. Diese summiert über alle einzelnen Loss-Funktions \(l(\theta)\) für jeden Graphen im Trainingsset und teilt durch die Anzahl der Graphen im Trainingsset. Dabei sieht die Funktion für die einzelnen Graphen so aus: $$ l(\theta) = \underset{\pi \in S_{\mathcal{C}}}{inf} - \sum_{i\in V} \log{o_{i,\pi(y_i)}}. $$ Hier ist \(S_{\mathcal{C}}\) die Permutationsgruppe aus \(\mathcal{C}\) Elementen. \(\mathcal{C}\) ist die Anzahl der möglichen Communities. Das \(inf\) sorgt dafür, dass das am meisten vorkommende Label mit der kleinsten Zahl belegt wird, das am zweit häufigsten vorkommende Label mit der zweit kleinsten Zahl und so weiter, sodass das Labeling Eindeutig ist (die Benennung der Labels der Community spielt keine Rolle, stattdessen in erster Linie die Erkennung dieser). Weiter beschreibt \(o_{i,c} = p(y_i = c \mid \theta,G)\) die bedingte Wahrscheinlichkeit, dass Knoten \(i\) in Community \(c\) ist, unter Voraussetzung von Graph \(G\) und aktuellen Trainingsparametern \(\theta\). Je besser also beim Trainieren des Modells die berechneten Labels \(y_i\) mit denen der im Trainingsset gegebenen Labels übereinstimmen, desto höher ist die Summe in der Loss-Funktion und desto niedriger ist dann der Funktionswert der Loss-Funktion.
Erklärung der Loss-Funktion im Video
4. Anwendung
Wir haben unsere Implementierung auf einer bereits Existierenden von der “Distributed (Deep) Machine Learning Community” aufgebaut und diese modifiziert. Dabei benutzen wir als Programmiersprache Python. Außerdem haben wir verschiedene Libraries benutzt:
- Pytorch (eine verbreitete Library für Deep-/Machine-Learning)
- dgl (eine auf Pytorch aufbauende Library für Graphen)
- networkx (zur Visualisierung der Graphen)
4.1 Bewertung
Wir haben die oben beschriebene Implementierung auf drei verschiedenen Datensätzen laufen gelassen:
- Kleiner Graph: 80 Knoten
- Mittlerer Graph: 3000 Knoten
- Großer Graph: 30000 Knoten
Diese wurden mit dem Stochastic Block Model (SBM) zufällig generiert.
Wir konnten folgende Resultate erzielen:
1. Kleiner Graph
[epoch 00] loss 0.667 | overlap 0.245 | forward time 0.446s | backward time 0.240s
[epoch 01] loss 0.710 | overlap 0.140 | forward time 0.612s | backward time 0.289s
[epoch 02] loss 0.546 | overlap 0.388 | forward time 0.371s | backward time 0.165s
[epoch 03] loss 0.548 | overlap 0.393 | forward time 0.286s | backward time 0.166s
[epoch 04] loss 0.617 | overlap 0.335 | forward time 0.284s | backward time 0.151s
[epoch 05] loss 0.542 | overlap 0.483 | forward time 0.276s | backward time 0.182s
[epoch 06] loss 0.490 | overlap 0.610 | forward time 0.355s | backward time 0.136s
[epoch 07] loss 0.528 | overlap 0.575 | forward time 0.254s | backward time 0.138s
[epoch 08] loss 0.502 | overlap 0.605 | forward time 0.259s | backward time 0.153s
[epoch 09] loss 0.551 | overlap 0.508 | forward time 0.284s | backward time 0.156s
[epoch 10] loss 0.449 | overlap 0.673 | forward time 0.436s | backward time 0.250s
[epoch 11] loss 0.500 | overlap 0.613 | forward time 0.444s | backward time 0.214s
[epoch 12] loss 0.427 | overlap 0.685 | forward time 0.395s | backward time 0.162s
[epoch 13] loss 0.571 | overlap 0.467 | forward time 0.327s | backward time 0.192s
[epoch 14] loss 0.453 | overlap 0.642 | forward time 0.325s | backward time 0.220s
[epoch 15] loss 0.432 | overlap 0.668 | forward time 0.360s | backward time 0.250s
[epoch 16] loss 0.459 | overlap 0.640 | forward time 0.509s | backward time 0.398s
[epoch 17] loss 0.464 | overlap 0.628 | forward time 0.298s | backward time 0.280s
[epoch 18] loss 0.582 | overlap 0.450 | forward time 0.232s | backward time 0.131s
[epoch 19] loss 0.440 | overlap 0.648 | forward time 0.369s | backward time 0.217s
2. Mittlerer Graph:
[epoch 00] loss 0.713 | overlap 0.034 | forward time 0.705s | backward time 1.959s
[epoch 01] loss 0.609 | overlap 0.103 | forward time 0.536s | backward time 1.126s
[epoch 02] loss 0.620 | overlap 0.139 | forward time 0.576s | backward time 1.160s
[epoch 03] loss 0.584 | overlap 0.180 | forward time 0.597s | backward time 1.257s
[epoch 04] loss 0.567 | overlap 0.234 | forward time 0.675s | backward time 1.270s
[epoch 05] loss 0.555 | overlap 0.268 | forward time 0.509s | backward time 1.142s
[epoch 06] loss 0.552 | overlap 0.321 | forward time 3.546s | backward time 5.484s
[epoch 07] loss 0.527 | overlap 0.378 | forward time 0.660s | backward time 1.618s
[epoch 08] loss 0.546 | overlap 0.324 | forward time 0.609s | backward time 1.285s
[epoch 09] loss 0.534 | overlap 0.341 | forward time 0.565s | backward time 1.289s
[epoch 10] loss 0.530 | overlap 0.375 | forward time 0.573s | backward time 1.229s
[epoch 11] loss 0.568 | overlap 0.286 | forward time 0.547s | backward time 1.272s
[epoch 12] loss 0.514 | overlap 0.423 | forward time 1.046s | backward time 1.546s
[epoch 13] loss 0.512 | overlap 0.428 | forward time 0.616s | backward time 1.331s
[epoch 14] loss 0.505 | overlap 0.449 | forward time 0.601s | backward time 1.224s
[epoch 15] loss 0.497 | overlap 0.484 | forward time 0.535s | backward time 1.169s
[epoch 16] loss 0.497 | overlap 0.484 | forward time 0.551s | backward time 1.294s
[epoch 17] loss 0.484 | overlap 0.550 | forward time 0.530s | backward time 1.227s
[epoch 18] loss 0.477 | overlap 0.562 | forward time 0.654s | backward time 1.274s
[epoch 19] loss 0.469 | overlap 0.593 | forward time 0.939s | backward time 1.841s
3. Großer Graph:
[epoch 00] loss 0.838 | overlap 0.009 | forward time 6.016s | backward time 17.572s
[epoch 01] loss 0.848 | overlap 0.004 | forward time 6.982s | backward time 19.535s
[epoch 02] loss 0.833 | overlap 0.007 | forward time 5.529s | backward time 15.605s
[epoch 03] loss 0.848 | overlap 0.006 | forward time 8.039s | backward time 20.535s
[epoch 04] loss 0.813 | overlap 0.013 | forward time 5.233s | backward time 15.431s
[epoch 05] loss 0.813 | overlap 0.018 | forward time 7.766s | backward time 19.036s
[epoch 06] loss 0.824 | overlap 0.015 | forward time 6.632s | backward time 19.079s
[epoch 07] loss 0.832 | overlap 0.013 | forward time 4.914s | backward time 14.639s
[epoch 08] loss 0.825 | overlap 0.018 | forward time 5.118s | backward time 13.980s
[epoch 09] loss 0.805 | overlap 0.024 | forward time 5.735s | backward time 13.666s
[epoch 10] loss 0.802 | overlap 0.027 | forward time 4.820s | backward time 14.045s
[epoch 11] loss 0.851 | overlap 0.011 | forward time 4.658s | backward time 14.097s
[epoch 12] loss 0.790 | overlap 0.037 | forward time 4.782s | backward time 13.421s
[epoch 13] loss 0.812 | overlap 0.027 | forward time 4.761s | backward time 13.390s
[epoch 14] loss 0.816 | overlap 0.020 | forward time 4.785s | backward time 13.757s
[epoch 15] loss 0.782 | overlap 0.042 | forward time 4.667s | backward time 13.437s
[epoch 16] loss 0.782 | overlap 0.040 | forward time 5.512s | backward time 13.700s
[epoch 17] loss 0.792 | overlap 0.038 | forward time 5.929s | backward time 13.337s
[epoch 18] loss 0.775 | overlap 0.051 | forward time 4.411s | backward time 12.866s
[epoch 19] loss 0.776 | overlap 0.050 | forward time 5.189s | backward time 13.053s
Oben sind mit “epoch” die Epochen gemeint. Eine Epoche beim Training ist gleichbedeutend damit, dass der Komplette Datensatz einmal vorwärts und rückwärts durch das Neuronale Netz geschickt wurde. Mit dem kleinen, mittleren und großen Graph wurde jeweils 20 Epochen trainiert. Außerdem beschreibt loss den Wert der oben beschriebenen Loss-Funktion. Man erkennt leicht, dass der Wert sich bei allen drei Graphen mit steigender Epochenzahl wie gefordert minimiert.
Man kann in der zweiten Chart erkennen, dass der Loss-Wert beim großen Graph wesentlich höher liegt, als bei den beiden anderen, und auch langsamer absinkt. Das heißt, dass, je größer der Graph ist, auch länger beziehungsweise öfter trainiert werden muss, um ein ausreichend gutes Ergebnis zu erzielen.
4.2 Visualisierung der gefundenen Communities
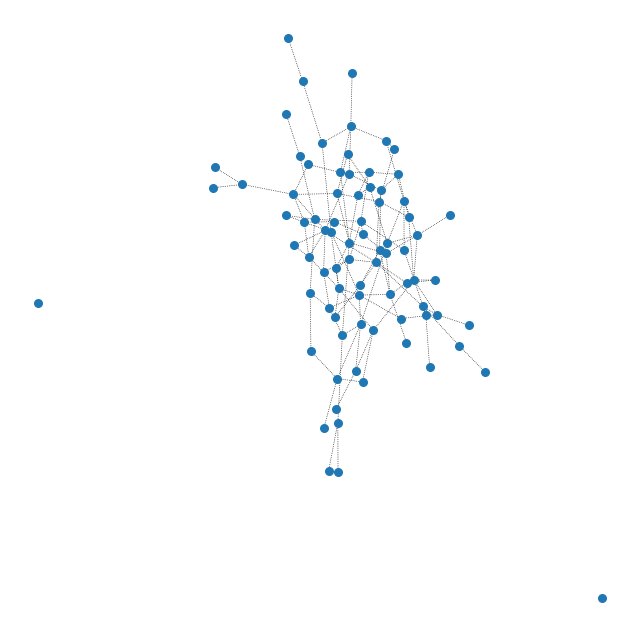
Beispielhaft haben wir je einen Graphen der kleinen und mittleren Graphenklasse visuell Dargestellt, einmal ohne Labels, also vor der Anwendung des Algorithmus und einmal nach der Anwendung des Algorithmus mit Labels, welche in entsprechenden Farben codiert sind.
Abbildung 2: Kleiner Graph vor Anwendung des Algorithmus
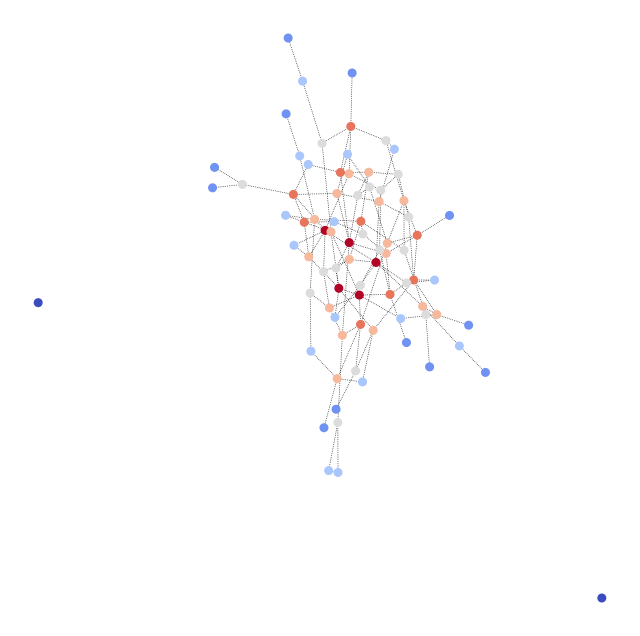
Abbildung 3: Kleiner Graph nach Anwendung des Algorithmus mit farbig hervorgehobenen Communities
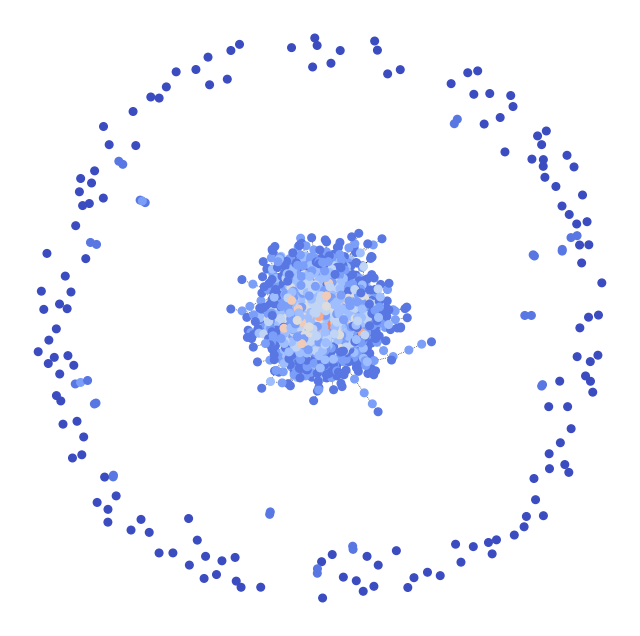
Abbildung 4: Mittlerer Graph vor Anwendung des Algorithmus
Abbildung 5: Mittlerer Graph nach Anwendung des Algorithmus mit farbig hervorgehobenen Communities
5. Zusammenfassung/Ausblick
Zusammenfassend lässt sich sagen, dass mit dem Line Graph Neural Network (LGNN) ein Algorithmus beziehungsweise Modell aus dem Deep Learning effektiv Ergebnisse liefert und somit Communities in verschiedenen Graphen erkennt. Jedoch existieren noch Grenzen. Gerade auf großen Graphen steigt mit steigender Knotenzahl auch der Rechenaufwand beim Trainieren des Algorithmus. Somit benötigt man eine hohe Rechenkapazität und dementsprechend leistungsfähige Maschinen. Auch benötigt man bei dieser Art der Community Detection zumindest zum Trainieren einige bereits gelabelte Graphen. Des Weiteren steigt der Trainingsaufwand mit der Anzahl von Knoten im Graph an, sodass bei gößeren Graphen über mehr Epochen trainiert werden muss.
Da jedoch gerade im Feld Deep Learning im Moment im Kontext der künstlichen Intellignez besonders intensiv geforscht wird, sind in Zukunft sicherlich noch viele neue Modelle zuerwarten, welche sicherlich auch effizienter sein werden.
6. Referenzen
- Tran, P. V. (2018). Learning to Make Predictions on Graphs with Autoencoders. 2018 IEEE 5th International Conference on Data Science and Advanced Analytics (DSAA), 237–245. https://doi.org/10.1109/DSAA.2018.00034
- Khan, R. A., & Kleinsteuber, M. (2020). Epitomic Variational Graph Autoencoder. ArXiv:2004.01468 [Cs, Stat]. http://arxiv.org/abs/2004.01468
- Han, F. (2019). Tutorial on Variational Graph Auto-Encoders. In Medium. https://towardsdatascience.com/tutorial-on-variational-graph-auto-encoders-da9333281129
- Chen, Z., Li, X., & Bruna, J. (2018). Supervised Community Detection with Line Graph Neural Networks. ArXiv:1705.08415 [Stat]. http://arxiv.org/abs/1705.08415