Erweiterung OCDA auf vorzeichenbehaftete Netzwerke (2)
| Valentin Baumann | Stefan Bleß | ||
|---|---|---|---|
| RWTH Aachen University | RWTH Aachen University | ||
| valentin.baumann@rwth-aachen.de | stefan.bless@rwth-aachen.de |
Abstract
Soziale Netzwerke haben in den letzten Jahren stets an Bedeutung gewonnen. Viele dieser Netzwerke verfügten anfangs ausschließlich über positive Verbindungen zwischen Personen, beispielsweise indem sie befreundet sind. Doch auch negative Verbindungen sind mit der Zeit immer relevanter geworden, wie Blockierungen, Sperrungen oder andere Anzeichen von Feindschaft beziehungsweise Misstrauen. Bisherige Overlapping Community Detection Algorithmen (OCDA) haben nur positive Verbindungen berücksichtigt. In dieser Ausarbeitung werden wir bekannte OCDA sozialer Netzwerke auf vorzeichenbehaftete Netzwerke erweitern und dabei näher untersuchen. Insbesondere der Attractor-Algorithm weist im Vergleich zu anderen OCDA auf vorzeichenbehafteten Netzwerken eine sehr gute Modularität auf.
Keywoards
Soziale Netzwerke, Communities, Overlapping Communities, Vorzeichenbehaftete Netzwerke, Attractor
Inhaltsverzeichnis
Einleitung
Positive und negative Verbindungen innerhalb eines sozialen Netzwerkes lassen sich durch vorzeichenbehaftete Netzwerke charakterisieren und darstellen. Dabei bilden die Personen eines sozialen Netzwerkes die Knoten eines Graphen, deren Verbindung mit einer gewichteten Kante mit positivem beziehungsweise negativem Vorzeichen versehen ist.
Vorzeichenbehaftete Netzwerke sind mit den bisherigen Algorithmen oft schwer greifbar, jedoch spiegeln diese die Realität in den meisten Fällen genauer wieder, da sie anders als die rein positiven Verbindungen einen Unterschied zwischen Feindschaft und und dem Fehlen einer Meinung miteinbeziehen können. Beides wird ohne Vorzeichen durch das Fehlen einer Kante implementiert. Um bestehende Algorithmen auf vorzeichenbehaftete Netzwerke zu erweitern, besteht ein möglicher Ansatz daraus, das soziale Netzwerk in mehrere Cluster aufzuteilen und diese auf soziale Ausgeglichenheit zu prüfen, das heißt jeder Zyklus in den jeweiligen Teilgraphen besitzt ausschließlich positive Kanten. In der Realität lässt sich dieses ideale Ergebnis nicht immer erreichen, so dass weitere Kennzahlen zur Bewertung solcher Cluster benötigt werden. Diese Kennzahlen sind unter anderem durch die sogenannte Frustration (Traag & Bruggeman, 2009) oder auch Modularität (Gómez et al., 2009) gegeben. Die Frustration definiert die Abweichung vom Idealgraph und die Modularität gibt den Grad an um welchen das Clustering sich signifikant von einem Zufallsergebnis abhebt. Dabei ist die Frustration zu minimieren und die Modularität zu maximieren.
In diesem Paper wird der Erweiterung des Attractor-Models (Shao et al., 2015) auf vorzeichenbehaftete Netzwerke Aufmerksamkeit geschenkt. Das grundlegende Prinzip basiert darauf die Modularität als vereinfachte Form mittels der sogenannten Intimacy \(I\) zwischen jeweils zwei Knoten zu implementieren. Dabei steigt diese nach (Chen et al., 2020), wenn eine gleiche Gewichtung zwischen beiden Knoten zu dritten besteht, beziehungsweise sinkt, wenn diese sich unterscheidet. Die Idee dahinter erinnert an das Sprichwort, der Feind meines Feindes sei mein Freund, welches sich im Kontext der OCDA meist bestätigt, da generell Comunities nach außen negativ und nach innen positiv gewichtete Kanten besitzen. In der mathematischen Umsetzung bedeutet das:
\[I(u,v,t+1)=I(u,v,t)+CI(u,v,t)+DI(u,v,t)+EI(u,v,t)\]Wobei \(CI\), \(DI\) und \(EI\) jeweils die Einflüsse gemeinsamer, generell verbundener und exklusiver Knoten darstellen. \(u\) und \(v\) sind, wie auch im Rest dieser Arbeit, zwei beliebige Knoten. \(t\) stellt den Iterations- beziehungsweise Zeitschritt dar, denn die Intimacy wird iterativ berechnet, weshalb Algorithmen die sie nutzen als Evolutionary Algorithms (EA) bekannt sind.
Verwandte Arbeiten
Erste Anwendungen von OCDA auf sozialen Netzwerken mit ausschließlich positiven Kanten wurden zum Beispiel von (Girvan & Newman, 2002) durchgeführt. Als Grundlage dazu dienten Daten aus der American College Football League. In dieser Arbeit werden wir den Attractor Algorithm, einen bekannten OCDA auf nicht-vorzeichenbehafteten Netzwerken, auf vorzeichenbehaftete Netzwerke erweitern und mit anderen OCDA vergleichen. Diese Erweiterung wurde ebenfalls in (Chen et al., 2020) mit den Daten aus der American College Football League erprobt.
Darüber hinaus werden wir die Kennzahlen Frustration und Modularität ausführlich einführen, was ebenfalls in (Cai et al., 2016), (Traag & Bruggeman, 2009) und (Gómez et al., 2009) behandelt wird. Um das Kürzen wesentlicher Faktoren durch positive und negative Gewichte zu vermeiden, muss bei der Übertragung der Definition von Netzwerken mit ausschließlich positiven Gewichten auf vorzeichenbehaftete Netzwerke einiges beachtet werden. Insbesondere bei der Modularität gibt es verschiedene Ansätze das klassische Konzept auf vorzeichenbehaftete Netzwerke zu übertragen. In dieser Ausarbeitung folgen wir der Ausführung von (Gómez et al., 2009).
In (Traag & Bruggeman, 2009) werden zusätzlich die erforschten Verallgemeinerungen auf vorzeichenbehaftete Netzwerke auf Kriegsdaten nach dem Mauerfall angewandt, worauf wir hier als Beispiel-Anwendung verweisen möchten. Eine weitere Anwendung findet mit der Weiterentwicklung des Attractors Algorithms aus (Shao et al., 2015) in (Chen et al., 2020) statt, die wir in dieser Ausarbeitung ebenfalls betrachten werden. Zudem wird in (Chen et al., 2020) ein Vergleich mit anderen OCDA durchgeführt. Diese anderen OCDA sind durch DEC (Chen et al., 2016) sowie DBAS (Wu et al., 2016) gegeben.
Methodik
Grundlagen und Notation
Soziale Netzwerke können durch Graphen dargestellt werden und werden daher mit \(G = (V,E)\) bezeichnet, wobei \(V\) die Menge der Knoten, das heißt der Personen eines Netzwerkes, und \(E\) die Menge der ungerichteten Kanten, das heißt der Verbindungen zwischen den Personen, ist. Zudem gibt es eine Funktion \(g \colon E \mapsto \mathbb{R}\), welche jeder Kante ein Gewicht zuordnet und damit stärkere sowie schwächere Bindungen charakterisiert. Bei der Einführung der Grundlagen und Notation von Communities gehen wir analog zu (Cai et al., 2016) vor. Wir definieren
als die Menge der positiven beziehungsweise negativen Verbindungen zwischen den Personen des sozialen Netzwerkes. Es bezeichne zudem \(n := |V|\) die Anzahl der Personen des sozialen Netzwerkes und \(A \in \mathbb{R}^{n\times n}\) die Adjazenzmatrix des sozialen Netzwerkes, welche durch
\[A(u,v) := \begin{cases} g(\{u,v\})&\text{, falls } \{u,v\} \in E \\ 0&\text{, sonst} \end{cases}\]für alle \(u,v \in V\) gegeben ist. Da wir ungerichtete Graphen betrachten, ist die Adjazenzmatrix symmetrisch.
Im weiteren Verlauf wird der Grad von Knoten benötigt, der für jedes \(u \in V\) durch \(d_u := \vert\{\{u,v\} \in E \ \vert \ v \in V\}\vert\) definiert ist. Der Grad eines Knotens gibt somit die Anzahl der ein- sowie ausgehenden Kanten eines Knotens an. Der Grad eines sozialen Netzwerkes \(d\) entspricht dem Mittelwert über alle Grade von Knoten des Netzwerkes, das heißt es gilt
\[d := \frac{1}{|V|}\displaystyle\sum_{u \in V}{d_u}.\]Von großer Bedeutung in sozialen Netzwerken sind die Communities, deren Definition wir ebenfalls einführen wollen. Dazu sei \(C \subseteq V\). \(C\) heißt eine Community innerhalb des sozialen Netzwerkes \(G\), falls
\[\displaystyle\sum_{\substack{v \in C\\ \{u,v\} \in E^+}}{A(u,v)} > \sum_{\substack{v \in C\\ \{u,v\} \in E^-}}{|A(u,v)|}\]für alle \(u \in C\) gilt. Somit müssen für jede Person innerhalb einer Community mehr gewichtete positive als negative Verbindungen innerhalb der Community vorliegen.
Falls \(E^- = \emptyset\) gelten sollte, das bedeutet im sozialen Netzwerk \(G\) treten keine negativen Verbindungen zwischen Personen auf, so ist die oben beschriebene Charakterisierung einer Community bereits erfüllt, sobald alle Personen der Community mindestens eine Verbindung innerhalb der Community mit einer anderen Person haben. Daher ist in diesem Spezialfall nach (Cai et al., 2016) auch eine alternative Charakterisierung einer Community üblich: In einem nicht vorzeichenbehafteten Graphen \(G = (V,E)\) ist eine Teilmenge \(C \subseteq V\) eine Community, wenn
\[\displaystyle\sum_{v \in C}{A(u,v)} > \sum_{v \notin C}{A(u,v)}\]für alle \(u \in C\) gilt. Somit liegt in diesem Spezialfall eine Community vor, wenn alle Personen der Community mehr gewichtete Verbindungen innerhalb der Community als in das restliche soziale Netzwerk haben. Diese Charakterisierung einer Community ist in vorzeichenbehafteten Netzwerken nicht anwendbar.
Communities können verschiedene Strukturen aufweisen. Sie können zum Beispiel disjunkt oder auch überlappend sein. Wir werden uns im weiteren Verlauf auf die überlappenden Communities konzentrieren.
Es gibt verschiedene Kenngrößen um Communities zu bewerten und zu vergleichen. Wir wollen zunächst die Frustration einführen und definieren dazu die Identifikatorfunktion durch
\[\mathbb{I}_{C} \colon V \rightarrow \{0,1\}, \ v \mapsto \begin{cases} 1 &\text{, falls } v \in C \\ 0 &\text{, sonst} \end{cases}\]für eine Community \(C \subseteq V\). Zudem bezeichne \(\sigma(G) = \{C_1,\ldots,C_m\}\) eine Menge von Communities mit
\[\displaystyle\bigcup_{k=1}^{m}{C_k} = V.\]Dann ist durch
\[\mathcal{F}_\lambda(\sigma(G)) := \sum_{k=1}^{m}{\left ((1-\lambda) \cdot \sum_{\substack{u,v\in V\\ \{u,v\}\in E^+}}{A(u,v)\left (1-\mathbb{I}_{C_k}(u)\mathbb{I}_{C_k}(v)\right)} - \lambda \cdot \sum_{\substack{u,v\in V\\ \{u,v\}\in E^-}}{A(u,v)\mathbb{I}_{C_k}(u)\mathbb{I}_{C_k}(v)} \right )}\]laut (Cai et al., 2016) die Frustration des sozialen Netzwerkes unter einer gegebenen Aufteilung in Communities und mit einem Prioritätsfaktor \(\lambda \in [0,1]\) gegeben. Bei der Frustration werden die positiven Verbindungen aus einer Community in eine andere Community sowie die negativen Verbindungen innerhalb einer Community gemäß ihrer Gewichtung und dem Priorätsfaktor \(\lambda\) aufsummiert. Idealerweise sind Communities innerhalb der Community nur positiv und zwischen den Communities nur negativ verbunden, um den ursprünglichen Graphen in disjunkte Teilgraphen zu zerlegen, die jeweils sozial ausgeglichen sind. Bei einem sozial ausgeglichenem Graphen besitzt jeder Zyklus innerhalb des Graphen ausschließlich positive Kanten und somit können die bekannten OCDA auf diese Graphen angewandt werden. Jeder Summand in der Frustration charakterisiert eine Kante, die für dieses ideale Ergebnis problematisch ist und somit ist es unser Ziel eine Zerlegung des Graphen in Communities zu finden, die die Frustration minimieren. Ist \(\mathcal{F}_{\lambda}(\sigma(G))=0\), haben wir dieses ideale Ergebnis erzielt, da stets \(\mathcal{F}_{\lambda}(\sigma(G))\geq 0\) gilt. In der Realität wird dies jedoch nur selten erreicht.
Wählen wir \(\lambda := \frac{1}{2}\), so ergibt sich
\[\mathcal{F}_{1/2}(\sigma(G)) = \frac{1}{2} \sum_{k=1}^{m}{\left (\sum_{\substack{u,v\in V\\ \{u,v\}\in E}}{-A(u,v) \mathbb{I}_{C_k}(u)\mathbb{I}_{C_k}(v))} + \sum_{\substack{u,v\in V\\ \{u,v\}\in E^+}}{A(u,v)}\right )},\]wobei die letzte Summe unabhängig von \(\sigma(G)\) ist und somit für das Minimierungsproblem keine Rolle spielt. Für das Minimierungsproblem genügt es daher, da die Multiplikation mit einem Skalar darauf ebenfalls keinen Einfluss hat, in diesem Fall
\[\displaystyle -\sum_{k=1}^{m}{\sum_{\substack{u,v\in V\\ \{u,v\}\in E}}{A(u,v) \mathbb{I}_{C_k}(u)\mathbb{I}_{C_k}(v)}}\]zu untersuchen. Die Anwendung dieses Minimierungsproblems ist nach (Cai et al., 2016) sinnvoll und üblich, so dass wir die Frustration ebenfalls im weiteren Verlauf in dieser Gestalt betrachten werden.
Neben der Frustration, die zur Bewertung von Communities genutzt werden kann, gibt es zudem die Modularität. Gemäß (Cai et al., 2016) und (Gómez et al., 2009) ist diese auf Graphen mit ausschließlichen nicht-negativen Gewichten gegeben durch
\[Q(\sigma(G)) := \frac{1}{2\omega}\sum_{k=1}^{m}{\sum_{u,v \in V}{\left ( A(u,v)- \frac{1}{2\omega} \mathbb{I}_{C_k}(u)\mathbb{I}_{C_k}(v)\sum_{v' \in V}{A(u,v')}\sum_{u'\in V}{A(u',v)} \right )}},\]wobei \(\omega := \sum_{u,v \in V}{A(u,v)}\) die Menge aller Gewichte der Kanten des Graphen darstellt. Bei gerichteten Graphen müsste der Faktor 2 vor \(\omega\) in der Definition der Modularität entfernt werden. Der Term \(\frac{1}{2\omega}\sum_{u \in V}{A(u,v)}\) entspricht der Wahrscheinlichkeit, dass der Knoten \(v\) zufällig mit einem anderen Knoten innerhalb des Netzwerkes durch eine Kante verbunden ist. Bei der Berechnung der Modularität werden somit die tatsächlichen mit den erwarteten Verlinkungen innerhalb eines sozialen Netzwerkes ins Verhältnis gesetzt. Als Kenngröße für Communities wird dabei versucht die Modularität zu maximieren.
Für vorzeichenbehaftete Netzwerke kann diese Definition nicht einfach übernommen werden, da sich positive und negative Gewichte aufheben können. Daher betrachten wir wie in (Gómez et al., 2009) die Modularität getrennt für positive und negative Verbindungen:
\[Q(\sigma(G))^+ := \frac{1}{2\omega^+}\sum_{k=1}^{m}{\sum_{\substack{u,v \in V \\ \{u,v\} \in E^+}}{\left ( A(u,v)- \frac{1}{2\omega^+} \mathbb{I}_{C_k}(u)\mathbb{I}_{C_k}(v)\sum_{\substack{v' \in V \\ \{u,v'\} \in E^+}}{A(u,v')}\sum_{\substack{u'\in V \\ \{u',v\} \in E^+}}{A(u',v)} \right )}}\]und
\[Q(\sigma(G))^- := \frac{1}{2\omega^-}\sum_{k=1}^{m}{\sum_{\substack{u,v \in V \\ \{u,v\} \in E^-}}{\left ( |A(u,v)|- \frac{1}{2\omega^-} \mathbb{I}_{C_k}(u)\mathbb{I}_{C_k}(v)\sum_{\substack{v' \in V \\ \{u,v'\} \in E^-}}{|A(u,v')|}\sum_{\substack{u'\in V \\ \{u',v\} \in E^-}}{|A(u',v)|} \right )}}\]mit
\[\displaystyle\omega^\pm := \sum_{\substack{u,v \in V\\ \{u,v\} \in E^\pm}}{|A(u,v)|}.\]Die Modularität auf vorzeichenbehafteten Netzwerken ist somit durch
\[Q(\sigma(G)) := \frac{2\omega^+}{2\omega^++2\omega^-}Q(\sigma(G))^+ - \frac{2\omega^-}{2\omega^++2\omega^-} Q(\sigma(G))^-\]gegeben.
D-Attractor
Der “Dynamic-Attractor-Algorithm” (Chen et al., 2020) ist eine Weiterentwicklung des vorherigen Attractor-Models. Im Gegensatz zu diesem können jedoch auch negative Vorzeichen miteinbezogen werden. Er ist in zwei Schleifen eingeteilt, welche jeweils über alle Knoten laufen. Die erste Schleife erstellt den Anfangsgraphen mit den Gewichtungen der Kanten. Hierzu wird die Adjazenzmatrix benötigt. Die zweite Schleife implementiert dann das eigentliche Clustering anhand eines weiterentwickelten Attractor-Models. Dies geschieht über die rekursive Berechnung der Intimacy.
Die Ähnlichkeit \(sim_{uv}\) zwischen zwei Knoten \(u\) und \(v\) wird modelliert durch
\[sim_{uv}= \begin{cases} \lambda_1 \times N^+_1 + \lambda_2 \times N^+_2, & A(u,v)>0,\\ \lambda_1 \times N^-_1 + \lambda_2 \times N^-_2, & A(u,v)<0,\\ 0, & A(u,v)=0 \end{cases},\]wobei \(\lambda_i\) den Einfluss des \(i\)-Sprungs auf die Ähnlichkeit darstellt und folgendermaßen berechnet wird:
\[\lambda_i=\frac{1}{d^i}, \ (i=1,2).\]Zudem bezeichnen \(N^+_1\) sowie \(N^-_1\) die Anzahl der positiv bzw. negativ gewichteten Sprünge der Länge 1, wobei ein Sprung von \(u\) nach \(v\) der Länge \(n\) einen Weg der Länge \(n+1\), welcher in \(u\) beginnt und in \(v\) endet, darstellt. Somit sind
und durch
ist die Anzahl der positiv bzw. negativ gewichteten Sprünge der Länge 2 gegeben. Bei der Berechnung von \(N^+_1\) geht unter anderem die Faustregel “Der Feind meines Feindes ist mein Freund” ein.
Beim D-Attractor ist die rekursive Gestaltung der Intimacy \(I\) als Evolutionary Algorithm gegeben. Somit ist es von großer Bedeutung, die Adjazenzmatrix \(A\) zu gewissen Zeitpunkten \(t\) zu betrachten, was wir im folgenden durch \(A(u,v,t)\) darstellen werden. Um Ähnlichkeit zum Zeitpunkt \(t\) zu definieren, betrachten wir die Definitionen aus den Gleichungen 2 und 3 erneut für einen Zeitpunkt \(t\), das heißt \(N^+_{1,t}\) charakterisiert den Einfluss der positiven Sprünge der Länge 1 zum Zeitpunkt \(t\), bei \(N^-_{1,t}\) und \(N^\pm_{2,t}\) wird gleich verfahren. Dies wird benötigt um den Graphen vor dem Clustering zu modellieren und die Ähnlichkeit aus Gleichung 1 zur Ähnlichkeit
\[sim^t_{uv}= \begin{cases} \lambda_1 \times N^+_{1,t}+ \lambda_2 \times N^+_{2,t}, & A(u,v,t)>0,\\ \lambda_1 \times N^-_{1,t}+ \lambda_2 \times N^-_{2,t}, & A(u,v,t)<0,\\ 0, & A(u,v,t)=0 \end{cases}\]zum Zeitpunkt \(t\) zu erweitern. Darüber hinaus normieren wie diese Ähnlichkeit aus Gleichung 4 und erhalten
\[s^t_{uv}= \begin{cases} \frac{sim^t_{uv}}{\sum_{u,v \in V, sim^t_{uv}>0} sim^t_{uv}}, & A(u,v,t)>0, \\ \frac{sim^t_{uv}}{\sum_{u,v \in V,sim^t_{uv}<0} sim^t_{uv}}, & A(u,v,t)<0, \\ 0, & A(u,v,t)=0 \end{cases}.\]Mittels \(\alpha\) lässt sich der Einfluss früher Knoten auf die momentane \(sim\) beliebig anpassen, das heißt für \(0 \leq \alpha \leq 1\) legen wir fest, ob der vorherige Zeitpunkt \(t-1\) oder der aktuelle Zeitpunkt \(t\) in Gleichung 5 von größerer Bedeutung sein sollen:
\[SIM(u,v,t)= \alpha \cdot s^{t-1}_{uv}+(1- \alpha )\cdot s^t_{uv}.\]Widmen wir uns nun der Berechnung der Intimacy (\(I\)), welche die Cluster erzeugen wird. Hohe Werte von \(I\) zeigen generell die Zugehörigkeit zu der gleichen oder einer ähnlichen Community. Diese wird iterativ mittels der folgenden Formel berechnet. Zum Zeitpunkt \(t=1\) gilt für alle Knoten \(I(u,v,1)=0.\) Für \(t > 1\) gilt dann
\[I(u,v,t):=I(u,v,t-1)+CI(u,v,t-1) +DI(u,v,t-1)+EI(u,v,t-1).\]\(DI\), \(CI\) und \(EI\) sind wie im generalisiertem Attractor definiert:
\(DI\) stellt den Einfluss verbundener Knoten auf die Intimacy dar:
\[DI(u,v,t)=\frac{SIM(u,v,t)}{d_u}+\frac{SIM(v,u,t)}{d_v}.\]\(CI\) berechnet den Einfluss gemeinsamer Nachbarn auf die Intimacy zwischen \(u\) und \(v\):
\[CI(u,v,t)=\sum_{\substack{x \in V \\ \{u,x\} \in E \\ \{v,x\} \in E}} \Biggl[ \frac{SIM(u,x,t) \cdot SIM(x,v,t)}{d_u}+\frac{SIM(v,x,t) \cdot SIM(x,u,t)}{d_v} \Biggr].\]Der Einfluss exklusiver Nachbarn wird durch \(EI\) implementiert:
\[EI(u,v,t)= \sum_{\substack{x \in V \\ \{u,x\} \in E \\ \{v,x\} \notin E}}\frac{SIM(u,x,t) \cdot SIM(x,v,t)}{d_u} + \sum_{\substack{y \in V \\ \{v,y\} \in E \\ \{u,y\} \notin E}}\frac{SIM(v,y,t) \cdot SIM(y,u,t)}{d_v}.\]Damit haben wir schlussendlich alle Grundlagen zur Einführung des D-Attractor-Algorithm geschaffen:
//Aus den Adjazenzmatrizen zum Zeitpunkt t und t-1 die Matrix SIM(u,v,t) berechnen
for each nodes in A(t), A(t-1) do {
Berechne sim(t-1) und sim(t) nach Gleichung 4;
Erhalte normalisierte Similarity Matrix s(t-1), s(t) nach Gleichung 5;
Erhalte gewichtete Similarity Matrix SIM(t) nach Gleichung 6;
}
/*Nachdem man jetzt alle Knoten und ihre Positionen
initialisiert hat werden sie nun geclustered*/
/*Implementierung des Attractors um die Cluster durch Iteration
zu erstellen. Diese gibt dem Algorithmus die Einordnung als EA*/
for each node in A(t) do {
Berechne CI(u,v,t-1), DI(u,v,t-1), EI(u,v,t-1) nach Gleichungen 8, 9 und 10;
Aktualisiere I(u,v,t) nach Gleichung 7;
}
Anwendungen
In Abbildung 1 wurden Daten der American College Football League mit dem D-Attractor-Algorithm auf Communities untersucht. Das Dataset beschreibt eine Vereinigung vieler amerikanischer und einer kanadischer Hochschulsportclubs. Es setzt sich zusammen aus 116 Schulen, die sich in 11 verbundenen und wenigen unabhängigen Vereinigungen aufgliedern. In dem Graphen repräsentieren die Knoten jeweils die einzelnen Hochschulteams. Die entstehenden Communities (hier jeweils eingefärbt) stellen die Vereinigungen dar. Ihre Abspaltungen sind dadurch bedingt, dass innerhalb der Vereinigungen mehr Spiele stattfinden als zwischen diesen. Somit gelingt das Clustering mittels des D-Attractors. Es sollte angemerkt werden, dass dieses Netzwerk nur positiv gewichtet ist, weshalb auch traditionelle Attractor-Algorithmen hier ebenfalls funktionieren würden (Chen et al., 2020).
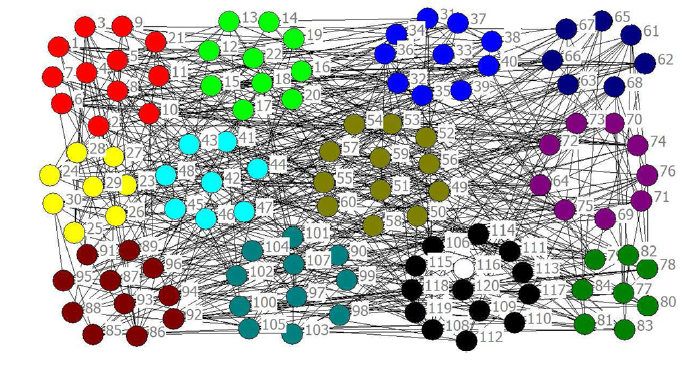
Abbildung 1: Ammerican College Football League, (Girvan & Newman, 2002), (Chen et al., 2020)
Die Abbildung 2 zeigt eine weitere Anwendung von Erweiterungen bekannter OCDA auf vorzeichenbehaftete Netzwerke. Diese steht zwar nicht mit dem Attractor-Algorithm in Verbindung, dient aber dennoch einer guten Veranschaulichung, weswegen wir dieses Beispiel aus (Traag & Bruggeman, 2009) hier anführen wollen.
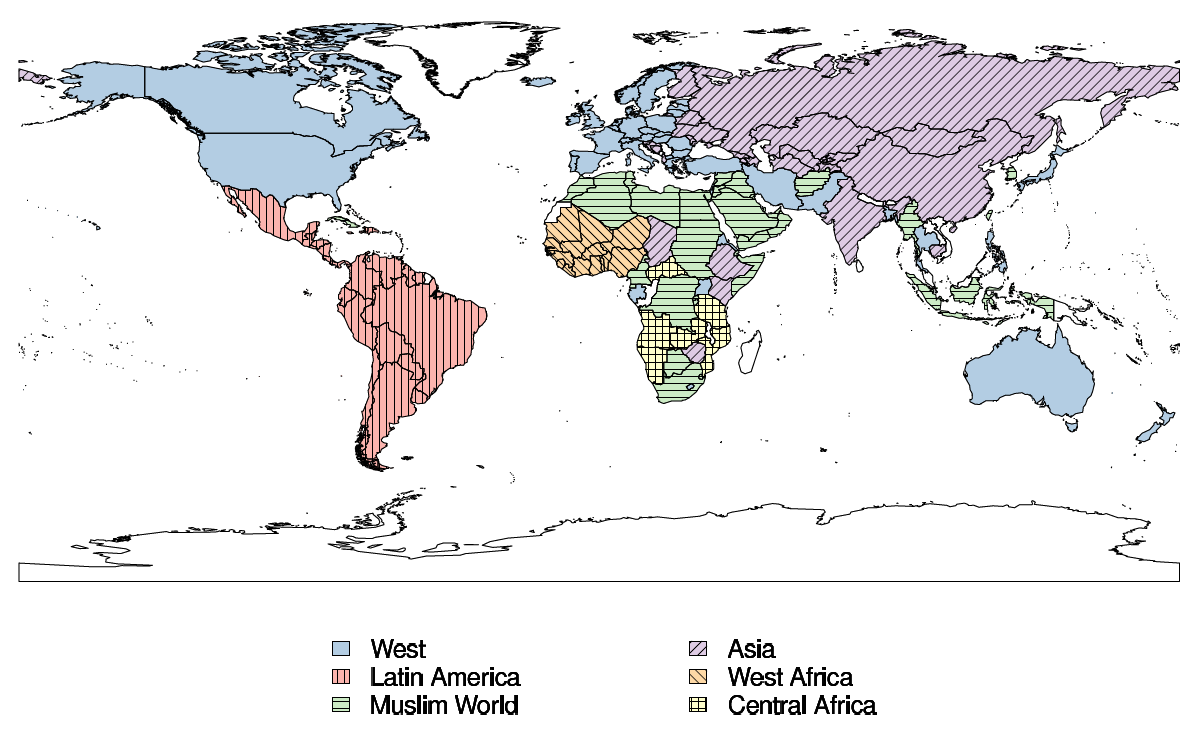
Abbildung 2: Weltkarte über militärische Allianzen von 1993 bis 2001, (Traag & Bruggeman, 2009)
Die Karte zeigt Communities von Staaten in den Jahren 1993 bis 2001. Als Grundlage dazu dienten bekannte militärische Allianzen als positive Verbindungen sowie Konflikte für negative Verbindungen. Solche Konflikte waren beispielsweise durch Grenzspannungen zwischen Kolumbien und Venezuela, Stationierungen chinesischer U-Boote auf japanischen Inseln oder das Eindringen türkischer Gruppen in irakisches Hoheitsgebiet gegeben. Diese konnten unterschiedlich schwer eingestuft werden, zum Beispiel als ‘keine militarisierte Aktion’ bis ‘zwischenstaatlicher Krieg’, so dass auch hier verschiedene Gewichtungen berücksichtigt wurden. Auch bei den positiven Verbindungen wurden Gewichtungen wie ‘Nichtangriffspakt’ oder ‘Verteidigungspakt’ berücksichtigt.
Die Nationen mit einer gleichen Farbe bilden in Abbildung 2 eine Community und es wurden insgesamt 161 Länder sowie 2517 Verbindungen zwischen diesen Ländern berücksichtigt. Die Vorgehensweise in (Traag & Bruggeman, 2009) basiert ebenfalls darauf, Teilgraphen zu finden, die innerhalb des jeweiligen Teilgraphen ausschließlich positive Verbindungen und zwischen den jeweiligen Teilgraphen nur negative Verbindungen aufweisen. Dies ist wiederum durch die Minimierung der Frustration möglich. In (Traag & Bruggeman, 2009) werden Hamilton-Wege innerhalb dieser Teilgraphen gebildet und mit einer gewissen Kennziffer versehen, die der Frustration im Verhältnis zu einem erwarteten Modell ähnlich ist. Diese Kennziffer zu minimieren ist nach den Ausführungen in (Traag & Bruggeman, 2009) äquivalent dazu, die Modularität zu maximieren. Laut (Traag & Bruggeman, 2009) liegt die Modularität \(Q\) in unserem Beispiel in Abbildung 2 bei \(Q = 0,561\).
Evaluation und Ergebnisse
Für die Analyse der Laufzeit werden die beiden Schleifen getrennt betrachtet werden. Die Berechnung von \(N^+_1\) und \(N^-_1\) (Gleichung 2) geschieht in folgender Weise: \(n_1\) ist definiert als die durchschnittliche Anzahl der gemeinsamer Nachbarn von zwei Knoten, und \(k\) als die Anzahl der Knoten. Hierfür beträgt die Laufzeit \(O(n_1 \cdot k^2)\).
Für \(N^+_2\) und \(N^-_2\) (Gleichung 3) wird das gleiche Verfahren angewandt. Daraus folgt die Komplexität der Gleichung 6 beträgt: \(O(n_2\cdot k^2)\). Die Gleichungen 8-11 werden durch die Gleichungen 5 und 6 dominiert. Daraus folgt die Komplexität der ersten Schleifen mit \(O(n_1\cdot k^2+n_2\cdot k^2)\). Da es für größere Netzwerke mehr Sprünge der Länge 2, als der Länge 1 gibt, ist die Komplexität in den meisten Fällen \(O(n_2 \cdot k^2)\).
Für die Analyse der zweiten Schleife, die den EA des Clusterings darstellt, gilt, dass die Berechnung von \(DI\) (Gleichung 8) ebenfalls die Laufzeit \(O(n_1 \cdot k^2)\) hat. Die Komplexität von \(CI\) kann vernachlässigt werden, da sie mit \(O(k^2)\) immer kleiner als \(DI\) ist. Für \(EI\) gilt \(O(e\cdot k^2)\), wobei \(e\) die durchschnittliche Anzahl der Knoten ist, die nur mit einem von zwei Knoten verbunden sind. Da es in komplexen Netzwerken mehr Kanten als Knoten gibt, folgt dass die Laufzeit des Clusterings \(O(n_1 \cdot k^2)\) beträgt.
Die Komplexität des gesamten Algorithmus entspricht \(O(n_2 \cdot k^2)+O(n_1 \cdot k^2)\), wie bereits in der Analyse des ersten Schleifen lässt sie sich effektiv mit \(O(n_2 \cdot k^2)\) beschreiben (Chen et al., 2020).
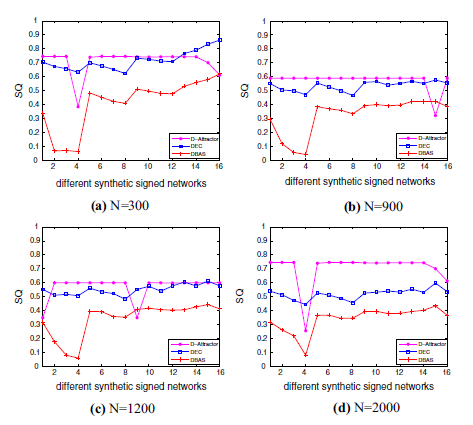
Die durchschnittliche Modularität des Algorithmus beträgt 0,7. Diese ist im Vergleich sehr gut. So hat zum Beispiel der DBAS (Wu et al., 2016) eine durchschnittliche Modularität von 0,5 und der DEC (Chen et al., 2016) ungefähr eine von 0,65. Diese wurden durch die Anwendung der drei Algorithmen auf je 16 synthetische Netzwerke mit 300, 600, 1200 und 2000 Knoten berechnet und die genauen Werte können der Abbildung 3 entnommen werden.
Abbildung 3: Vergleich mit anderen Algorithmen, (Chen et al., 2020)
Zusammenfassung und Ausblick
Der D-Attractor ist eine interessante Weiterentwicklung des generellen Attractor-Models um negative Vorzeichen in das Clustering miteinbeziehen zu können. Im Vergleich mit den beiden anderen angeführten Algorithmen schneidet er hinsichtlich der hohen Modularität sehr gut ab. Eine klare Schwäche ist jedoch, dass er - wie Attractor basierende Algorithmen generell - Probleme hat Overlapping Comunities zu finden und diese nicht auf Grund der potenziell geringeren Intimacy in einzelne Comunities zu verteilen. Dementsprechend bietet sich ein klares Ziel der zukünftigen Forschung den Algorithmus darauf zu erweitern. Momentan sollte man sich bei dem Einsatz des D-Attractors dieser Schwäche bewusst sein und ihn vor allem in Bereichen einsetzen, in denen Overlapping Comunities entweder selten sind, oder das Verfehlen ihrer Erkennung nur geringe Probleme verursacht. Ein möglicher Ansatz könnte darin bestehen eine weitere Variable einzuführen, welche in mehreren Durchläufen verändert wird um alle potenziellen Comunities zu finden und diese dann übereinander zu legen.
Referenzen
- Traag, V. A., & Bruggeman, J. (2009). Community detection in networks with positive and negative links. Physical Review. E, Statistical, Nonlinear, and Soft Matter Physics, 80(3 Pt 2), 036115. https://doi.org/10.1103/PhysRevE.80.036115
- Gómez, S., Jensen, P., & Arenas, A. (2009). Analysis of community structure in networks of correlated data. Physical Review, 80(1), 016114+. https://doi.org/10.1103/physreve.80.016114
- Shao, J., Han, Z., Yang, Q., & Zhou, T. (2015). Community Detection based on Distance Dynamics. In L. Cao, C. Zhang, T. Joachims, G. Webb, D. D. Margineantu, & G. Williams (Eds.), Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining: KDD’15 (pp. 1075–1084). https://doi.org/10.1145/2783258.2783301
- Chen, J., Liu, D., Hao, F., & Wang, H. (2020). Community detection in dynamic signed network: an intimacy evolutionary clustering algorithm. Journal of Ambient Intelligence and Humanized Computing, 11(2), 891–900. https://doi.org/10.1007/s12652-019-01215-3
- Girvan, M., & Newman, M. E. J. (2002). Community structure in social and biological networks. Proceedings of the National Academy of Sciences, 99(12), 7821–7826. https://doi.org/10.1073/pnas.122653799
- Cai, Q., Ma, L., Gong, M., & Tian, D. (2016). A survey on network community detection based on evolutionary computation. International Journal of Bio-Inspired Computation, 8(2), 84. https://doi.org/10.1504/IJBIC.2016.076329
- Chen, J., Wang, H., Wang, L., & Liu, W. (2016). A dynamic evolutionary clustering perspective: Community detection in signed networks by reconstructing neighbor sets. Physica A: Statistical Mechanics and Its Applications, 447, 482–492. https://doi.org/10.1016/j.physa.2015.12.006
- Wu, J., Zhang, L., Li, Y., & Jiao, Y. (2016). Partition signed social networks via clustering dynamics. Physica A: Statistical Mechanics and Its Applications, 443, 568–582. https://doi.org/10.1016/j.physa.2015.09.066