Jasmin Al Khateeb
RWTH Aachen University
jasmin.al.khateeb@rwth-aachen.de

Vanessa Bangert
RWTH Aachen University
vanessa.bangert@rwth-aachen.de

Jessica Pelz
RWTH Aachen University
jessica.pelz@rwth-aachen.de

Abstract

In der heutigen Zeit sind soziale Netzwerke kaum noch wegzudenken. Was früher über persönliche Interaktionen passiert ist, lagert sich mittlerweile in die sozialen Medien aus. So bilden sich soziale Netzwerke, welche, neben biologischen und technischen Netzwerken, mit Hilfe der Netzwerkanalyse untersucht werden können. Dabei lassen sich diese komplexen Strukturen von Communities in einem sozialen Graph repräsentieren und somit algorithmisch untersuchen.
Netzwerke der realen Welt weisen durch immer heterogene Communities eine hohe Komplexität auf, wodurch sich die Visualisierung ohne Informationsverlust als immer schwieriger herausstellt. Je komplexer die Strukturen, aufgrund von Fortschritt von Wissenschaft und Technik, werden, desto wichtiger ist es, die gefragten komplexen Systeme ästhetisch und für den Menschen durchschaubar darzustellen. Um eine zu starke Vereinfachung der Daten dabei zu vermeiden, ist man dazu übergegangen vielschichtige Daten durch Multilayer Netzwerke abzubilden. In der Netzwerktheorie wird deshalb an unterschiedlichen Visualisierungsmethoden gearbeitet um eine Menge von Beziehungen, die fortlaufend veränderlich ist, durch diese neue Art der Repräsentation zu visualisieren. Im Folgenden wird aufgezeigt, wie sich vielfältige Informationen geschickt und kompakt, auf unterschiedliche Arten, als Multilayer Netzwerke visualisieren lassen. Darüber hinaus wird Bezug auf die algorithmische Erstellung dieser Netzwerke genommen, sowie auf die open source Software MuxViz. Das Resultat dieser Übersichtsarbeit ist die Gegenüberstellung der Visualisierungsmethoden mit ihren Vor- und Nachteilen und die Betonung darauf, dass diese nach Kontext zu wählen sind. Dabei ist eine Kombination verschiedener Methoden häufig am naheliegendsten.
___

Inhaltsverzeichnis

1. Einleitung
2. Verwandte Arbeiten
3. Methodik
   1. Mathematische Darstellungsform
   2. Graphische Visualisierungsmethoden von Multilayer Netzwerken
      1. Zweidimensionale Darstellungen
         1. Zirkuläre Darstellung
         2. Achsenbasierte Knoten-Link Darstellung
         3. Chord Darstellung
         4. Kantenbündelung
         5. Matrix Darstellung
      2. Dreidimensionale Darstellungen
         1. knotengefärbter Graph
         2. kantengefärbter Graph
         3. 2,5-dimensionaler Ansatz
      3. Kombination von Methoden
   3. Algorithmische Positionierung der Knoten
      1. Fruchterman Reingold Algorithmus
      2. Kamada Kawais Modell
      3. Clustering Algorithmus
4. Evaluation
5. Zusammenfassung
6. Referenzen

---

1. Einleitung

Um schlichte Daten in Single Layer Netzwerken darzustellen, gibt es bereits eine Bandbreite an Möglichkeiten. Beispiele dafür sind Knoten und Kanten gefärbte Multigraphen, auf die im Verlauf der Arbeit noch genauer eingegangen wird. Diese dienen teilweise als Ausgangspunkt der graphischen Darstellung von Multilayer Netzwerken.
Die genaue Darstellungsart wird dabei nach den verschiedenen, für den Kontext relevanten, Vergleichskriterien gewählt. Sachverhalte wie unterschiedliche Parameter, Datensätze und Skalen sind dabei zu beachten.
Sobald man durch eine höhere Informationsdichte keine vereinfachte Darstellung durch Singlelayer Netzwerke nutzen kann, ohne dass relevante Informationen verloren gehen, besteht die Möglichkeit der Darstellung mit Hilfe von mehreren Layers im Graphen. Dies bietet die Chance der Klassifizierung unterschiedlicher Knoten und somit der Visualisierung von verschiedenen Beziehungsformen. Dadurch können umfangreichere Daten kodiert werden, als es bei der separaten Betrachtung von Layern möglich ist.

Die Visualisierung von Multilayer Netzwerken bietet vor allem im Bereich der Community-Erkennung die Möglichkeit, mit Hilfe der Analyse und Auswertung dieser Graphen, Gemeinschaften zu erkennen.
In Hinblick auf Communities können Knoten zum Beispiel die einzelnen Akteure im sozialen Netz darstellen. Durch eine farbliche Kodierung besteht dabei des Weiteren die Möglichkeit, jedem Akteur eine Rolle zuzuordnen. Gefärbte Kanten bieten die Möglichkeit der Visualisierung von zum Beispiel unterschiedlichen Beziehungsarten zwischen zwei Akteuren.
Befinden sich die Knoten und Kanten in verschiedenen Layern, können diese Layer noch weitere Aspekte, wie unterschiedliche Kommunikationskanäle, unterschiedliche Kommunikationszeiten und vieles mehr, darstellen. Wenn man von einem Single Layer zu einem Multilayer Netzwerk übergeht, ist es daher von entscheidender Bedeutung, wie die Layers, Knoten und Kanten aufgeteilt und angeordnet werden.
Betrachter können so einfacher Strukturen, die ähnlich zu Gemeinschaften sind, erkennen. Bei dieser Formulierung ist jedoch die Problematik der nicht existierenden allgemeinen Definition von “Gemeinschaft” zu berücksichtigen.
Im folgenden werden wir erst einen eigenen Datensatz einführen. Dadurch schaffen wir eine Vergleichbarkeit und können basierend darauf die unterschiedlichen Visualisierungsmethoden, unter zuhilfenahme eigener Abbildungen, übersichtlicher vorstellen . Dabei fangen wir mit vereinfachten zweidimensionalen Abbildungen an und gehen zu dreidimensionalen über.
Um ein Praxisbeispiel der theoretischen Visualisierungsmethoden aufzuzeigen, stellen wir danach die Software MuxViz vor und erläutern ihre Arbeitsweise, unter kurzem Einbezug der verwendeten Algorithmen. In der Evaluierung wird abschließend eine Tabelle mit allen Vor- und Nachteilen jeder Visualisierungsmethode präsentiert.

2. Verwandte Arbeiten

Die erste fundamentale Unterscheidung, die durch Fintan McGee, Mohammad Ghoniem, Guy Melançon, Benoit Otjacques, Bruno Pinaud in ihrer Arbeit mit dem Titel “The State of the Art in Multilayer Network Visualization” getroffen wird, ist die in ein- und mehrdimensionale Netzwerkdarstellungen (Mcgee et al., 2019). Diese sinnvolle Unterscheidung wird in unserer Arbeit auch erfolgen.

Ein weiterer Artikel, der als Grundlage diente, ist ein umfangreicher Übersichtsartikel, der die bereits zu diesem Zeitpunkt, vorhandene Literatur zusammenfasst und eine Zuordnung von Netzwerktypen zur Multilayer Netzdarstellungen vornimmt. (Kivelä et al., 2014)

Eine Verarbeitung von Entitäten in Multilayer Netzwerken sollte von Mitteln begleitet werden, die es ermöglichen, Daten zu analysieren, zu visualisieren und korrekte Erkenntnisse daraus zu gewinnen.
Eine solche Möglichkeit wird im Paper über die open source Software MuxViz (Manlio De Domenico, 2015) von Manlio De Domenico, Mason A. Porter und Alex Arenas vorgestellt.
Bei der Recherche zu unserer Arbeit stießen wir oft auf die Erwähnung der Software MuxViz. Diese bietet die Möglichkeit, Multilayer Netzwerke zu analysieren und zu visualisieren. Entscheidend dafür, dass wir diese Plattform vorstellen, ist die Möglichkeit der eigenen Implementierung eines Vereinfachungsalgorithmus und der interaktiven Visualisierungsmöglichkeit durch den Nutzer.

Ein aktuell relevantes Paper aus dem Jahre 2021 kombiniert den, auf Kräfte basierenden, Algorithmus (welcher auch bei MuxViz verwendet wird) mit dem hierarchischen Clustering-Algorithmus und schlägt eine Visualisierungsmethode vor, die die Eigenschaften der Multilayer Netzwerkstruktur verbessert zeigen kann.
Dabei werden durch Experimente an mehrschichtigen Netzwerkinstanzdaten die Wirksamkeit und Anwendbarkeit der Visualisierungsmethode überprüft (Shenhao & Ronghuan, 2021).

Unsere Arbeit soll einen Überblick über die verschiedenen, bereits entwickelten, Visualisierungsarten geben und sie gegeneinander abwägen. Dadurch soll dargelegt werden, für welchen Kontext sich welche Methode am besten eignet jedoch auch klar gemacht werden, dass man immer Abstriche in der Informationsdichte in Kauf nehmen muss. Dies spricht stark für die weitere Forschung und Entwicklung im Themengebiet der mehrdimensionalen Graphentheorie.

3. Methodik

3.1 Mathematische Darstellungsform

Zum schaffen eines Grundlegenden Verständnisses führen wir erst einmal die mathematische Definition von Single- und Multilayer Netzwerken ein. Single Layer Netzwerke dienen sowohl bei der mathematischen als auch bei der visuellen Verarbeitung als fundamentale Grundlage zur Erweiterung auf Multilayer Netzwerke.

Singlelayer Netzwerke

Bei einem einfachen Graph handelt es sich um ein Tupel (Kivelä et al., 2014)

• \(G = (V,E)\) mit Knotenmenge V und Kantenmenge E
• \(n = \vert V \vert\) ist die Anzahl von Knoten in G und \(m = \vert E \vert\) die Anzahl von Kanten.
• \(V = (v_{1}..v_{n})\) (endliche) Menge an Knoten
  
• \(EV \times V\) (endliche) Menge an Kanten, die Knoten miteinander verbinden und somit zueinander in Beziehung stellen
  

Multilayer Netzwerke

Um Systeme zu repräsentieren, die einen höheren Informationsgehalt darstellen sollen, besteht die Möglichkeit der Einführung einer weiteren Struktur. Die Layers sorgen dafür, dass der Graph aus mehreren Schichten besteht.
Ein Multilayer Netzwerk besteht damit aus (Kivelä et al., 2014)

• \(M = (V_{m},E_{m},V,L)\) mit
  
• \(V=(v_{1},v_{2},...,v_{n})\) (endliche) Menge an Knoten
  
• \(L\) Menge von Layern für jeden Aspekt (Aspekte: Interaktionen, Zeit…)
  
• \(E_{m} \times V_{m} \times V_{m}\) (endliche) Menge an Kanten (Layers der Nachbarknoten angeben: \(V_{m}\) statt V)
  

3.2 Graphische Visualisierungsmethoden für Multilayer Netzwerken

Der Hauptunterschied zwischen den verschiedenen Darstellungsarten von Multilayer Netzwerken liegt dabei bei den verwendeten Kriterien, nach denen die Knoten mit den Layern verknüpft werden und bei der Anordnung der Layers. Die meisten Visualisierungsmethoden basieren dabei auf der Technologie für Single Layer Netzwerke und sind somit in erster Linie auf diese ausgelegt. Eine Erweiterung, sodass sich mit der Visualisierungsmethode Multilayernetzwerke darstellen lassen, ist möglich, jedoch auch mit Aufwand und immern noch möglichem Verlust an Informationen verbunden.
Multilayer Netze können in ihrer topologischen Struktur Merkmale einer Gemeinschaft aufweisen. So sind durch die Visualisierung zum Beispiel Teilnetze zu erkennen, welche übergeordnete und untergeordnete Knoten enthalten. Dabei lokalisieren eng miteinander verbundene Knoten in einem Teilnetz eine Gemeinschaft in dem sozialen Netz, welches gerade visualisiert wird. Spärlich verbundene Knoten implizieren keine hohe Zusammengehörigkeit. Teilnetze können durch diese Knoten miteinander verbunden sein, das bedeutet zwei verbundene Knoten existieren in verschiedenen Gemeinschaften auf der gleichen Ebene. Anwendbar ist diese Darstellungsart also vor allem in Bezug auf die Detektierung von Communities in Netzwerken, die auf Datensätzen aus sozialen Netzwerken basieren. Mit der passenden Visualisierung kann der Betrachter des Multilayer Netzwerkes direkt relevante Information erkennen. Dabei kann sich, in einem begrenzten Bildschirmbereich, eine große Anzahl an Knoten und Kanten überlagern und kreuzen. Dies beeinträchtigt das Verständnis und die Erkennung der Struktur von möglichen Gemeinschaften. Aus diesem Grund ist es wichtig, dass diese graphische Darstellung nach den für den Kontext besten Möglichkeiten entsteht.
Im Folgenden werden unterschiedliche Darstellungsarten sowie deren algorithmische Entstehung veranschaulicht.
Den mathematischen Hintergrund dazu zu erläutern stellte sich dabei als schwierig heraus. Wie die Viusualisierungsmethoden durch Formeln mathematisch definiert werden ist in fast allen Fällen lediglich auf Single Layer Netzwerke spezifiziert. Dabei liegt die Annahme eines einfachen Graphen ohne mehrere Layer zugrunde. Eine mathematische Erweiterung auf Multilayer Netzwerke ist dadurch, bei weniger verbreiteten Methoden wie die zirkuläre Darstellung und der Achsen basierten Methode nicht zu finden.
Die Weiterentwicklung der genauen Implementierung der Visualisierungsmethoden von Multilayer Netzwerke ist also dringend nötig.

Verwendeter Datensatz

In dem von uns ausgedachtem verwendeten Beispieldatensatz geht es um Studierende unterschiedlichen Semesters, die auf verschiedene Arten miteinander vernetzt sind. In den folgenden Visualisierungsmethoden handelt es sich bei den Knoten um die Studierenden. Sind die Knoten gefärbt, beinhalten sie das Attribut, das Semester, des Studierenden. Die Kanten visualisieren die Vernetzung zwischen den einzelnen Studierenden, wobei eine Färbung für die jeweilige Plattform steht, über die die Studierenden, vernetzt sind.
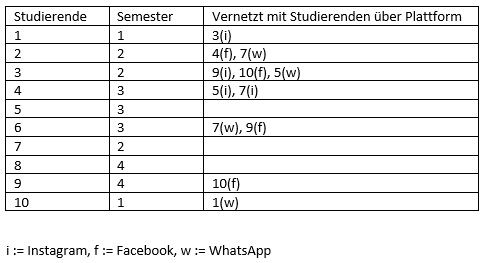Tabelle 1
Beispieldatensatz. 10 Studierende sind jeweils einem Semester zugeordnet und es wird gezeigt über welche sozialen Plattformen diese vernetzt sind.

3.2.1 Zweidimensionale Darstellung

Zirkuläre Darstellung

Eine mögliche Darstellungsart von Multilayer Netzwerken ist die als konzentrische Kreise. Hierbei steht jeder Kreis für einen Layer. Ein ähnliches Layout wird in der Ringansicht der open source software MuxViz verwendet (Manlio De Domenico, 2015), auf die im späteren Verlauf noch genauer eingegangen wird.
Diese Darstellungsart wird mit den Funktionalitäten einer Head Map verbunden. Die monochrome Variation von Sättigung oder Helligkeit einer Farbe kann somit in einer großen Menge an Daten schnell und intuitiv einen Überblick darüber schaffen wie stark ein Attribut ausgeprägt ist (Mcgee et al., 2019). Dies macht besonders auffällige Werte leicht erkennbar.
Eine mögliche Anordnung der Daten besteht daraus, jedem Knoten ein “Kuchenstück” des Kreises, den die Ringe bilden, zuzuordnen. Die Färbung dieser Ringbereiche kann durch unterschiedliche Kodierungen zu stande kommen und somit unterschiedliche Daten beinhalten und visualisieren (Bothorel et al., 2013).

In unserem Anwendungsbeispiel steht die Färbung der Ringe für die Häufigkeit, mit der ein Studierender eine soziale Plattform nutzt, um mit einem anderen Studierenden über diese verbunden zu sein (Abbildung 1).
Dafür ließe sich zum Beispiel die Funktion mit Hilfe von RGB Werten im Hexadezimalsystem defnieren. Dabei handelt es sich in unserem Beipsiel bei der Definitionsmenge der Funktion um die verschiedenen Anzahlen der Verbindungen über die soziale Plattformen. Diese werden auf die RGB Werte abgebildet (in unserem Fall visualisieren wir den Farbverlauf von blau). Dazu wird die kleinste Anzahl an Verbindungen und die größte Anzahl an Verbindungen wie folgt abgebildet:

\(min \rightarrow AAAAFF\)
\(max \rightarrow 0000FF\)

Zwischen diesen Werten ist die Funktion linear definiert.

Die einzelnen Ringe bilden die verschiedenen Plattformmöglichkeiten ab. Dabei ist jedoch nicht mehr ersichtlich, welche Studierenden genau miteinander verbunden sind. Eine zentrale Information geht damit in dieser Visualisierungsmethode verloren.
Eine weitere Information, die hierbei verloren geht, ist die über das Semester der Studierenden. Durch Umdefinierung der Schichten und Farbkodierung ließen sich jedoch auch die Semester als einzelne Ringe darstellen und die Färbung könnte indizieren, auf welcher Plattform der Studierende am meisten vertreten ist.
Durch die Benutzung der Heat Map Eigenschaft, liegt der Schwerpunkt bei dieser Darstellungsart auf der visuellen Korrelationsanalyse von der Ausprägung der Kantenattribute (Nutzung der verschiedenen Plattformen) über verschiedene Studierende hinweg (Mcgee et al., 2019) .
Eine Erweiterungsmöglichkeit wäre die Einführung einer Funktion, welche Metriken auf Ebene der Layer auf die Ringdicke in der Visualisierung abbildet.

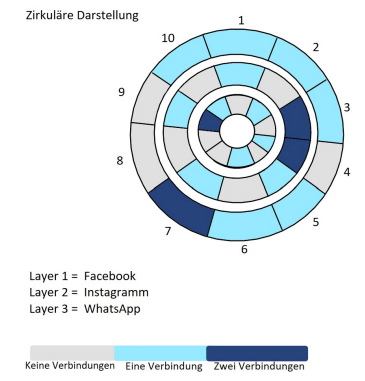Abbildung 1
Die einzelnen Segmente stellen hier die Studierenden dar. Die Layer werden von innen nach außen durchnummeriert. Die Anzahl an Verbindungen sind in der Legende kodiert.

Achsenbasierte Knoten-Link-Darstellung

Bei dieser Visualisierungsmethode werden Layer durch gerade Achsen dargestellt. Um Multilayer Netzwerke darzustellen werden mehrere Achsen parallel zueinander gesetzt. Diese achsenbasierte Visualisierung unterscheidet sich durch die Art der, durch die Achse dargestellten, Variablen. Zwei Vertreter der Achsenbasierten Darstellung ist der Parallel Node Link Band Ansatz und der Hive Plot Ansatz.(Mcgee et al., 2019)

Parallel Node Link Band Ansatz

Hierbei sind die Knoten gleichmäßig auf den parallelen Achsen angeordnet, die, durch den Knotentyp definierte, Layer darstellen.
Außerdem werden Kanten nur zwischen benachbarten Layern dargestellt (Ghani et al., 2013). Um die Verbindungen der Knoten innerhalb eines Layers zu visualisieren, muss eine separate Darstellung verwendet werden. Hier spielt die Anordnung der Knoten in einem Layer eine wichtige Rolle. Sie werden entweder nach Attributen der Kanten angeordnet oder die Reihenfolge wird durch Konnektivität zu anderen Ebenen festgelegt (Mcgee et al., 2019).

Bezogen auf unseren Datensatz steht jede Layer für ein Semester. Die Studierenden, die sich also auf dieser Achse befinden, sind dem Semester zugeordnet. Die Kanten zwischen den Knoten implizieren die gegebenen Verbindungen zwischen den Studierenden. In dieser Visualisierungsmethode geht jedoch die Information über die Plattform, über die, die Verbindung besteht, verloren. Außerdem können Verbindungen nur zwischen benachbarten Achsen und damit aufeinanderfolgenden Semestern dargestellt werden (Abbildung 2) und Verbindungen innerhalb eines Semesters müssen in einer weiteren Darstellung visualisiert werden.
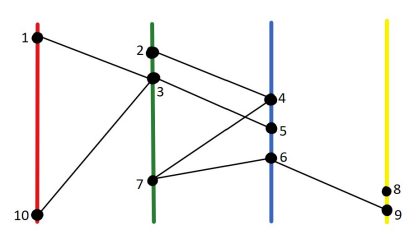Abbildung 2
rot = 1. Semester, grün = 2. Semester, blau = 3. Semester, gelb = 4. Semester

Hive Plot Ansatz

Die Achsen werden bei dieser Darstellungsform radial angeordnet (Krzywinski et al., 2012). Dabei werden Teilmengen von Knoten auf der Grundlage eines Algorithmus zur Knotenpartionierung auf separaten Achsen plaziert. Die Position eines Elements entlang seiner Achse wird dabei zum Beispiel basierend auf dem Knotengrad \(d_G(v)\) getroffen. Dieser ist definiert, als die Anzhal alles Kanten des Graphen \(G\) die an Knoten \(v\) grenzen.
In unserem Abbildungsbeispiel haben wir einfachheitshalber den Knotengrad mit der Nummerierung des Studierenden gleichgesetzt.
Auch hier werden Kanten nur zwischen benachbarten Layern angezeigt. Durch diese Visualisierung kann man vor allem Unterschiede in den Konnektivitätsmustern zwischen Schichten erkennen. Dabei kann es bei realen Anwendungsdaten dennoch zu einer visuellen Unübersichtlichkeit kommen. Deshalb besteht die Möglichkeit, Layer also eine Achse zu duplizieren, wenn die Beziehung zu einer nicht benachbarten Achse notwendig wird (siehe Abbildung 3, grüne und gelbe Achse).(Mcgee et al., 2019)

Durch diese Erweiterung der Achsendarstellung ist es möglich, auch die Verbindungen zwischen nicht aufeinanderfolgenden Semestern darzustellen. Dafür dupliziert man einfach die Semesterachsen und ordnet diese sinnvoll an.
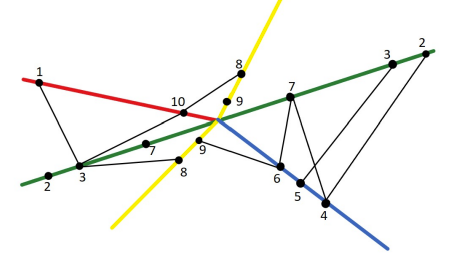Abbildung 3
rot = 1. Semester, grün = 2. Semester, blau = 3. Semester, gelb = 4. Semester
Hier können Achsen dupilizert werden, damit die Vernetzungen einzelner Layer ersichtlich wird.

Chord Diagramme

Ein Cord Diagramm besteht aus Bögen und Cords. Hier werden Layer als Bogen abgebildet, die bei ihrer Zusammensetzung einen Kreis bilden. Die Verbindung zwischen den Layern wird Chord genannt, welche Interaktionen zwischen den einzelnen Layern zeigen. Auch hier spielt die Farbe, sowie die Länge der Bögen und Chords eine Rolle, um verschiedene Beziehungen zu kennzeichnen und zu unterscheiden. Ein Nachteil dabei ist, dass diese Diagrammform nicht in der Lage ist Knoten abzubilden, die isoliert von den restlichen sind (siehe fehlender Knoten 8 in Abbildung 4).(Mcgee et al., 2019)
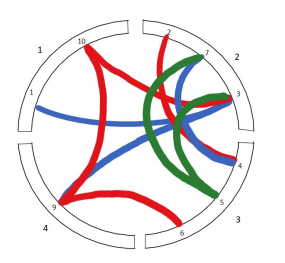Abbildung 4
In dieser Darstellung sind die Semester die äußeren Bögen. In diesen sind die zugehörige Studierenden aufgefasst, die eine Verbindung zu anderen Studierenden haben. Die Farben der Verbindungen sind die Plattformen (blau = Instagram, grün = WhatsApp, rot = Facebook).

Der mathematische Hintergund wird dabei in der Forschung für Single Layer Netzwerke definiert, wobei Ausgangspunkt ein gewichteter Graph \(G=(N,E,w)\) ist. Mit der Funktion \(w : E \rightarrow R_{> 0}\) welche einer Kante \(e \in E\) ein Gewicht \(w(e)\) zuordnet.
Eine mögliche Übertragung auf Multilayer Netzwerke wäre dabei die, für den Kontext sinnvolle, Kodierung von Knoten- oder Kantenattribute als Gewicht \(w(e)\) .
Ein Chord Diagram ist nun das Tupel \(G = (N,E,w),r,\phi,\chi)\) mit
\(G\) : der Single Layer Graph,
\(r\): der Radius des Graphen,
\(\phi : N \rightarrow (N,R_{> 0})\) : eine Funktion, die die Menge der Bögen des Chorddiagramms auf der Grundlage des Graphen G zurückgibt,
\(\chi : (n \in N, m \in N) \rightarrow (N,N,R_{> 0})\) : eine Funktion, die die Breite der Chords des Chorddiagramms für jedes Knotenpaar des Graphen zurückgibt (Jalali, 2016).
Durch sinnvolle Definierung dieser Funktion, lassen sich zum Beispiel die Bögenlängen an die Anzahl der, sich in dieser Layer befindlichen, Knoten anpassen und somit auf Multilayer Netzwerke erweitern. Oder auch die Breite der Chords, welche zwei Knoten miteinander verbindet, abhängig von zum Beispiel einer Beziehungsart machen.

Kantenbündelung

Um eine Übersichtlichkeit bei Knoten und Kanten basierten Visualisierungsmethoden schaffen zu können wird die Technik der Kantenbündelung angewandt, bei der alle Kanten in einer einzigen Visualisierung in einer ästhetisch ansprechenden Weise angeordnet werden. Kanten werden dabei nebeneinander gehalten, wenn sie einen gemeinsamen Pfad haben und Kantenkreuzungen werden vermieden (Mcgee et al., 2019) .
Dieser Ansatz ist nützlich, um Kanten aus mehreren Ebenen in einer einzigen Visualisierung darzustellen. Zu Grunde liegt somit ein kantengefärbter Graph. Dies ist aber nur möglich, wenn es keine Unterteilung der Knoten zwischen den Ebenen gibt.
In unserem Fall geht damit die Information über das Semester der Studierenden verloren. Diese Darstellungsform ist anwendbar, ohne Reduzierung, auf nur die Informationen einer Ebene und unabhängig davon, ob die Kanten zwischen oder innerhalb einer Ebene liegen.
Kanten werden also auf Grundlage des Typs gruppiert und zum Beispiel in einem kreisförmigen Layout dargestellt. 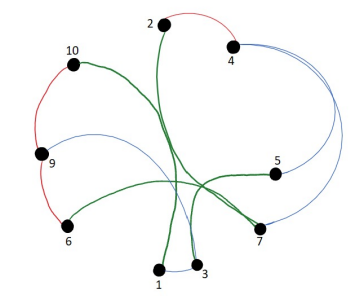Abbildung 7
kantengefärbter Graph (rot = Instagram, blau = Facebook, grün = WhatsApp), die die Vernetzung der Studierenden über gegebene Plattformen zeigt.

Matrixbasierte Darstellung

Bei großen und/oder dichten Graphen hat sich gezeigt, dass matrixbasierte Darstellungen für viele Aufgaben, mit Ausnahme der Pfadfindung (diese ist nicht möglich), besser lesbar sind als Knoten-KantenDiagramme.
Hier werden Knoten als Zeilen und Spalten einer 2-Wege-Tabelle angelegt. Eine Verbindung zwischen zwei Knoten wird oft als ein Rechteck am Schnittpunkt der zugehörigen Zeile und Spalte dargestellt. Die Art der Verknüpfung wird durch verschiedene Farben dargestellt. Auf diese Weise wird das Problem der Kantenüberschneidung bei den Standarddarstellungen von Knotenverbindungen vollständig vermieden.
In unseren Abbildungen steht die Farbe, der Felder in der Matrix, für die soziale Plattform, über die, die Verknüpfung besteht. Seriationsalgorithmen sorgen für die Anordnung von Zeilen und Spalten, um die Erkennung von Verknüpfungsmustern in der Matrixansicht zu optimieren.
Bei Vorhandensein mehrerer Layer kann der Vergleich von Verknüpfungsmustern zwischen vielen Ebenenpaaren für den Analytiker nützlich sein. Ein Ansatz besteht darin, kleine Vielfache von Matrixansichten nebeneinander zu legen (Mcgee et al., 2019).

Mathematische Definition:

(Bianconi, 2018)
Für die Abbildung 5 benutzen wir die Darstellung einer Superadjazenzmatrix. Die enthält Intra- also auch Interverbindungen eines Mulitlayernetzwerks (also Verbinungen innerhalb und außerhalb einer Layer).

Gegeben sei eine Menge an Knoten V = {i|i \(\in\) {1, 2, … , N}}.
Eine Layer definieren wir als \(\alpha\) mit dem Indize (i, \(\alpha\)). Der Index i beschreibt den bestimmten Knoten. Der Index \(\alpha\) gibt an in welcher Layer der Knoten i liegt. \(\alpha\) := 1, 2,…, M.
Somit erhalten wir eine Menge \(V_{\alpha} = \{(i, \alpha)| i \in \{1,2, ... N_{\alpha} \}\}\) die die Menge der Knoten beschreibt welche sich in der Layer \(\alpha\) befinden.
Ein Netzwerk \(G_{\alpha}\) beschreiben wir durch die \(N_{\alpha} \times N_{\alpha}\) Adjazenzmatrix \(a[\alpha,\alpha]\). Welches dann die Abbildung 6 beschreibt, da dort nur Intraverbindungen enthalten sind, da wir die einzelnen Layer seperat betrachten und diese nur Verbindungen innerhalb der Layer haben.
Wir erhalten dann eine Matrix A der Form A:=

\[\begin{pmatrix} a^{[1,1]} & a^{[1,2]} & \ldots & a^{[1,M]}\\ a^{[2,1]} & a^{[2,2]} & \ldots & a^{[2,M]}\\ \vdots & \vdots & \ddots & \vdots \\ a^{[M,1]} & a^{[M,2]} & \cdots & a^{[M,M]} \end{pmatrix}\]

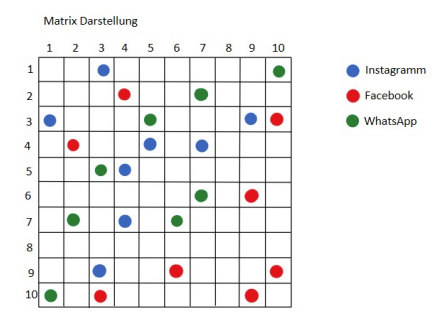ein Eintrag in der Matrix zeigt die Verbindung der Studierenden der Spalte und Zeile. Diese Abbildung zeigt die Gesamtsituation unseres Datensatzes und unterscheidet nicht nach Semestern.
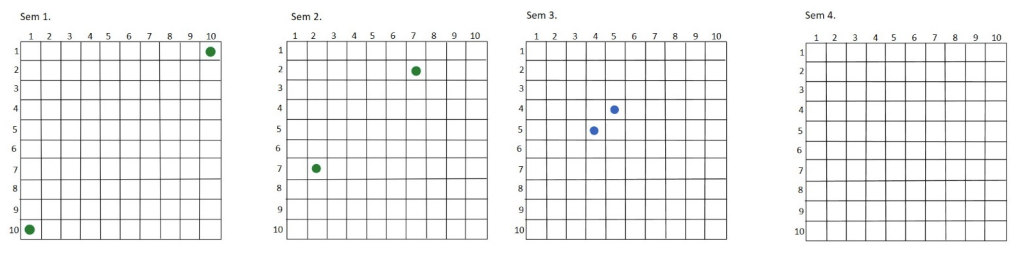Abbildung 6
durch die Aufteilung der Knotenattribute (in unserem Beispiel das Semester) erfolgt ein geringer Informationsgewinn da nur intralayer Kanten sichtbar werden

Eine sinnvolle Ergänzung der Matrixdarstellung wäre es, auf der freien Diagonalen (Einträge \(a_{ij}\) mit \(i=j\) in Abbildung 5 die Information des Knotenattributs (das Semester) zu vermerken.
Unser Praxisbeispiel die Software MuxViz verwendet Matrizen, um Statistiken auf Layer-Ebene zusammenzufassen, um dem Analysten eine Vorstellung von der Ähnlichkeit der Ebenen zu vermitteln (Manlio De Domenico, 2015).

3.2.2 Dreidimensionale Darstellungen

In einem zweidimensionalen Layout können Communities trotz Visualisierung nicht so leicht erkannt werden. Knoten, die eigentlich zu verschiedenen Layern gehören, sind in der 2D-Ebene miteinander verflochten und die Kantenüberschneidung ist problematisch. Deshalb bietet sich in manchen Kontexten eine 3-dimensionale Darstellung an. Wir sagen, dass ein Multilayer Netzwerk knotenausgerichtet (oder “vollständig vernetzt”) ist, wenn alle Schichten alle Knoten enthalten (Abbildung 9):
\(V_M=V\times L_1 \times \ldots \times L_d\).
Ein mehrschichtiges Netz ist schichtgetrennt, wenn jeder Knoten in höchstens einer Schicht existiert (Abbildung 8):
\((u,\alpha),(u,\beta) \in V_M \Rightarrow \alpha = \beta\)

Ausgangspunkt: knotengefärbter Graph

Knotengefärbte Netze sind Graphen, in denen jeder Knoten genau eine Farbe hat:
\(G_c=(V_c,E_c,C,\mathcal{X})\)
Wobei \(V_c\) und \(E_c\) die Knoten und Kanten sind, \(C\) die Menge der möglichen “Farben” ist (wobei jede Farbe eine mögliche kategoriale Bezeichnung für die Knoten ist) und \(\mathcal{X}:V_c \rightarrow C\) eine Funktion ist, die die Farbe jedes Knotens angibt.
Bei Netzen mit mehreren Typen und heterogenen Netzen ist die Zuordnung zu knotenfarbigen Netzen offensichtlich, da jeder Typ nun als “Farbe” bezeichnet wird.
Bei der Überführung eines Knoten gefärbten (Multi)Graphs in ein Multilayer Netzwerk werden die Knoten mit gleichen Farben in der gleichen Schicht gruppiert. Die Kanten sind dabei dieselben wie im ursprünglichen Netz. Und können keine Kantenattribute kodieren.
Indem man jede Schicht als eine Knotenfarbe betrachtet (siehe Abbildung 7 (b)) defniert man:
\(V=V_c, L=C, V_M=\{(u,c)\in V \times L | \mathcal{X}(u) =c \}\) und
\(E_M=\{((u,c_1),(v,c_2)) \in V_M \times V_M|(u,v) \in E_c\}\)
(Kivelä et al., 2014).
Da jeder Knoten nur eine einzige Farbe hat, ist dieses mehrschichtige Netz disjunkt.
Der Fokus, in solchen Graphen liegt dabei auf der Nutzung der Topologie des Systems aus einer knotenbasierten Perspektive, da der zugrundeliegende einschichtige Graph eines Systems mit heterogenen Knoten repräsentiert.
Sollte es nicht wichtig sein, die Knotennamen beizubehalten, kann man alternativ die Knoten so umbenennen, dass die Knoten in jeder Schicht bei 1 beginnen (siehe Abbildung 8 (c)).
Dazu definieren wir eine Funktion \(\gamma :V_c\rightarrow \{1, \ldots ,n_c\}\), die jeden Knoten mit einer ganzen Zahl zwischen 1 und der maximalen Anzahl von Knoten \(n_c\) mit derselben Farbe so benennt, dass zwei Knoten derselben Farbe nicht denselben Namen haben
\(\gamma(u)=\gamma(v)\Rightarrow \mathcal{X}(u) \neq \mathcal{X}(v))\) (Kivelä et al., 2014).
Daraus folgt, dass

\(V=\{1,\ldots,n_c\}, L=C, V_M=\{(\gamma(u),c) \in V \times L|\mathcal{X}(u)=c,u \in V_c\}\) und \(E_M=\{((\gamma(u),c_1),(\gamma(v),c_2)) \in V_M \times V_M|(u,v) \in E_c\}\).



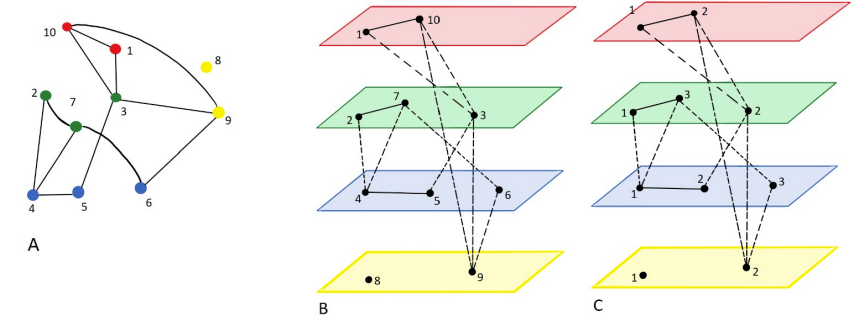Abbildung 8
(a) Knotengefärbter Graph
(b) Darstellung des Graphen aus (a) mit Hilfe von verschiedenen Schichten, wobei die Nummerierung übernommen wird
(c) weitere Repräsentation des Graphen aus (a) mit Hilfe von Layern, wobei hier die Knoten in jeder Schicht bei 1 anfangend neu benannt werden (dadurch benötigt man auch die Information der Schicht, um einen speziellen Knoten genau zu lokalisieren).

Es ist sowohl typisch als auch praktisch, für schichtübergreifende Kanten eine andere Semantik zu verwenden als für Kanten, die innerhalb einer einzelnen Schicht bleiben. Dies wird in der Abbildung durch durch gezogene beziehungsweise gestrichelte Kanten verdeutlicht. Daher ist es oft sinnvoll, die Menge der Kanten in schichtinterne Kanten
\(E_A= \{((u,\alpha),(v,\beta)) \in E_M | \alpha=\beta \}\)
und schichtübergreifende Kanten
\(E_C=E_M∖E_A\)
zu unterteilen.

Bezug auf Beispieldatensatz

Bei dieser Darstellungsart gruppiert man die Studierende nach Semestern, wobei die Kanten nur indizieren können, ob sich zwei Studierende (innerhalb und über die Semester hinaus) kennen, eine weitere Unterscheidung in die Plattformart der Verbindung ist nicht möglich.

Ausgangspunkt: kantengefärbter Graph

Knoten können in Multilayer Netzwerken aber auch in mehreren Schichten gleichzeitig existieren.
Bei dieser Darstellungsart von (Multi)Graphen sind die Kanten, entsprechend den verschiedenen Arten von Beziehungen, die sie repräsentieren gefärbt und stellen demzufolge Systeme mit heterogenen Verbindungen da. Dies wird als Triplet \(G_e=(V, E,C)\) definiert, wobei \(V\) die Knotenmenge, \(C\) die Farbmenge (die zur Kennzeichnung der Kanten dient) und \(E \subseteq V \times V \times C\) die Kantenmenge ist (Hammoud & Kramer, 2020) .

Bei der Visualisierung durch so ein Multilayer Netzwerk, werden die Knoten des ursprünglichen Netzes auf die verschiedenen Layer übertragen. Kanten gleicher Farbe gehören dabei zu der gleichen Ebene. Dabei lassen sich die Daten der Knotenattribute nicht mitverarbeiten. Somit stellen die Schichten die verschiedenen Aspekte der Beziehungen im Netz da. Dabei ist es möglich, dass jede Schicht eine Teilmenge oder die vollständige Menge an Knoten enthält. Zwei Knoten können dabei nur mit einer Kante jeder Farbe verbunden werden.
Man kann kantengefärbte Multigraphen außerdem verwenden, um eine Folge von Graphen darzustellen, in denen alle Knotenmengen gleich sind (d. h. \(V_\alpha=V_\beta =V\) für alle \(\alpha,\beta\) ), indem man jedem Graphen eine weitere eindeutige Farbe zuordnet (Berlingerio et al., 2011).
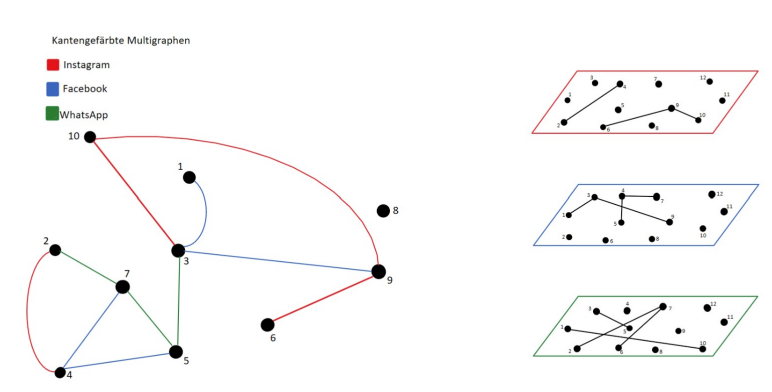Abbildung 9
Links: Kanten gefärbten Graphen. Die Kanten zeigen jetzt die Plattformen worüber die Studierenden vernetzt sind. Rechts: Die Überführung des kantengefärbten Graphen in ein Multilayernetzwerk. Ebenen sind hier die Kanten, also die Plattformen. Und alle Knoten des Graphen finden sich in jeder Schicht wieder.

Bezug auf Beispieldatensatz

Durch diese Darstellungsart ist die Unterscheidung in die einzelnen Platformen, durch die, die Verbindungen bestehen, möglich. Dabei weisen die Studierende selbst keine Attribute mehr auf, das heißt, dass die Information über die Semester verloren geht. Dabei ist es möglich, dass sich alle Knoten in jeder Schicht wiederfinden oder auch nur Teilmengen von Studierenden, die etwas mit dieser Plattform zu tun haben, also zu der dazugehörigen Layer, gehören.

Wie in Abbildung 9 zu erkennen, werden nur Schichtinterne Kanten angezeigt. In der Literatur wird jedoch in der Regel implizit davon ausgegangen, dass die Knoten in irgendeiner Weise mit ihren Gegenstücken in anderen Schichten verbunden sind (Hammoud & Kramer, 2020).
Nach der Überführung zu dieser Darstellungsvariante handelt es sich um einen knotenorientierten Graphen. Der Fokus liegt hier auf der Interferenz seiner Komponenten und der Dynamik des Netzwerkes. Vor allem bei der Untersuchung von verschiedenen Aspekten desselben Systems erweist sich diese Verwendung als effizient. (Hammoud & Kramer, 2020)

2,5-dimensionaler Ansatz

Inspiriert von der Mehrschichtigkeit einiger Problembereiche materialisiert der 2,5D-Ansatz die Schichten als durchsichtige parallele 2D-Ebenen in einem dreidimensionalen Layout. Es trennt die Verbindungen innerhalb der Ebenen von denen zwischen den Ebenen und bietet somit eine einfachere Erkennung von Pfaden innerhalb des Netzwerks. Die 3D-Navigation ist dabei erforderlich, damit der Benutzer seine Perspektive auf die Daten ändern und visuelle Verdeckungsprobleme lösen kann. (Mcgee et al., 2019)

Sind also so viele Kanten vorhanden, dass Gefahr besteht den Überblick zu verlieren, ist ein Lösungsansatz nicht alle Kanten anzuzeigen. Der Benutzer wählt durch Interaktion selbst welche Kanten angezeigt werden. Dadurch könnte man in unserem Beispiel den Fokus auf nur ein oder zwei Semester legen.
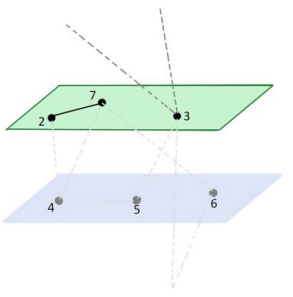Abbildung 10
Es existieren 2 Ebenen, eine ist halbdurchsichtig. Die Layer stellen hier das jeweilige Semester dar, somit ist ein Fokus auf den Aspekt eines Semsters gelegt.

Kombination von Methoden

Da ersichtlich ist, dass man mit verschiedenem Informationsverlust, je nach Visualisierungsmethode, rechnen muss, wird in der realen Anwendung meistens eine Kombination verschiedenster Methoden und Abbildungen genutzt.
Wir haben Multilayer Netzwerke mit mehreren Arten von Kanten und Multilayer Netzwerke mit mehreren Arten von Knoten vorgestellt. Es ist auch möglich, dass Netze diese beiden Merkmale aufweisen. Ein natürlicher Weg, ein solches Netz auf Multilayer Netze abzubilden, besteht darin, die Farben von Knoten und Kanten als separate Aspekte zu betrachten.
Solche Multilayer Netzwerke wurden unter den Bezeichnungen heterogene Informationsnetze (Davis et al., 2011) und gekoppelte Zellennetze mit mehreren Pfeilen (missing reference) untersucht.
Eine Zusammensetzung von verschiedenen Visualisierungsmethoden ist zum Beispiel die NodeTrix Methode (Mischung aus NodeLink und Matrix-Darstellung) (Henry et al., 2007). Hier werden Communities als eigene Matrizen dargestellt. Um Beziehungen innerhalb einer Community abzubilden, wird die Adjazenz Matrix verwendet. Bei Beziehungen zwischen Communities werden dann einfache Kantenverbindungen verwendet.

3.3 Algorithmische Positionierung der Knoten

Das Praxisbeispiel, welches in vielen Papern erwähnt wird, ist die open source Software MuxViz, welche Multilayer Netzwerke, auf verschiedenste Weisen visualisiert und analysiert. Beispielsweise als Edge-Colored Network, Interconnected Mulitlex, Interdependent Network, General Mulitlayer und unterschiedlichste layer layouts wie One-line layered, Mulit-line layered, force directed oder einer Matrix (Manlio De Domenico, 2015).
Dabei wird fossiert eine Standard mehrdimensionale Knoten Link Visualisierung verwendet.
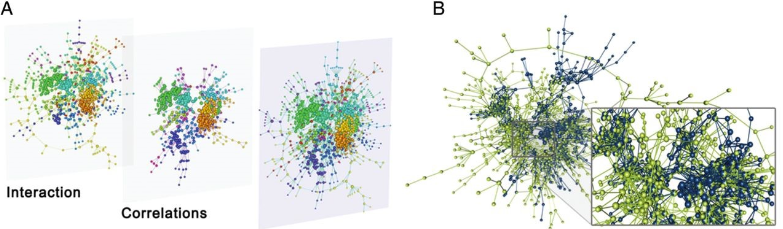Abbildung 11
Beispiel Visualisierungen von MuxViz
A: Nutzung expliziet definierter Layer
B: Zeigt den Ausgangspunkt (Kanten gefärbter Multigraph) für ein Multilayer Netzwerk
(Manlio De Domenico, 2015)

Damit diese Darstellungsarten in MuxViz nützlich sind, ist es wichtig, Knoten und Kanten so anzuordnen, dass eine Übersichtlichkeit des Sachverhalts herrscht. Die genaue Position der Knoten auf den Layern wird dabei durch Algorithmen berechnet. Bei MuxViz werden zwei kräftebasierte Layout Algorithmen kombiniert, um die Position der Knoten zu bestimmen.
Dabei wird zuerst der im folgenden erläuterte Fruchterman-Reingold Algorithmus angewendet.
Die entstehende Ausgabe wird dann für den Kamada-Kawai-Algorithmus genutzt. Dadurch wird eine bessere räumliche Trennung der Knoten im endgültigen Layout erzielt.
Durch unterschiedliche Beabsichtigung der Nutzung von Multilayer Netzwerken bietet MuxViz die Option andere Layout Möglichkeiten zu wählen. Dadurch kann zum Beispiel jede Layer unabhängig sein oder die Knotenstandorte mit Hilfe jeder einzelnen Ebene oder einer Aggregation über eine beliebige Teilmenge von Layern bestimmt werden (Manlio De Domenico, 2015).
In der Netzwerktopologie ist der Force-Directed-Algorithmus, der kraftgesteuerte Algorithmus, die derzeit häufigste verwendete Technologie zur Visualisierung der komplexen Netzstrukturdaten (Kivelä et al., 2014).

Verfahren zur Anordnung der Knoten in einem kraftorientiertem Layout

Kraftorientierte Layouts basieren darauf, dass auf Knoten und Kanten Kräfte, definiert durch zum Beispiel Hierarchisierung der Kanten, wirken und ausgehen. Diese werden mit Hilfe von Algorithmen miteinander verrechnet und das Ergebnis ist im Optimalfall ein sinnvoll, ästhetisch angeordneter Graph.
Ausgelegt ist dieses Verfahren in erster Linie auf Single Layer Netzwerke. Es lässt sich jedoch auch auf Multilayer Netzwerke wie folgt erweitern: Die ersten beiden Elemente eines mehrschichtigen Netzes M ergeben einen Graphen \(G_M = (V_M,E_M)\), so dass man ein Multilayer Netzwerk als einen Graphen interpretieren kann, dessen Knoten auf eine bestimmte Weise beschriftet sind. (siehe Abb. 2(b)).
Diese Beobachtung macht es einfach, einige der grundlegenden Konzepte von Single-Layer Netzen auf Multilayer Netze zu verallgemeinern. So lässt sich zum Beispeil ein gewichtetes Multilayer Netzwerk M definieren, indem wir Gewichte für die Kanten im zugrundeliegenden Graphen \(G_M\) definieren. Das bedeutet jeder Kante eines Netzes wird mithilfe einer Funktion \(w : E_M \rightarrow R\) eine reelle Zahl zugeordnet. Diese kann als Input für den kraftorientierten Algorithmus genutzt werden und somit ein Maß der anziehenden Kraft einer Kante sein.

Fruchterman Reingold Algorithmus

Jeder Knoten besitzt eine abstoßende Kraft.
Jede Kante besitzt eine anziehende Kraft.
Der Algorithmus lässt sich in zwei Phasen aufteilen.

1. Die Kraftvektoren, die auf einen Knoten wirken, aufsummieren.
   
2. Knotenposition (aufgrund der Kraftvektoren) neu bestimmen.
   Berücksichtigt wird, dabei noch die Größe der Zeichenfläche.
   
   \(f_{anziehende}(d) = \frac {d^{2}}{k} ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ d = |v-u| \\ ~~ \\ f_{abstoßend}(d) = -\frac {k^{2}}{d} ~~~~~~~~~~ k = C * \sqrt {\frac {Width * Hight}{ |V|}}\)
   
   

\(d:\) Entfernung zweier Knoten \((u,v)\).
\(k:\) optimale Entfernung zweier Knoten.
\(C:\) Konstante wird experimentell ermittelt.
Gesamtaufwand des Algorithmus \(O(n^2)\).
(Neef, 2009)
(Thomas M. J. Fruchterman, 1991)

Durch die Anwendung des Fruchterman Reingold Algorithmus sind die Kanten gleichmäßig lang und Knoten aus verschiedenen Gemeinschaften können zu weit verstreut liegen. In Folge ist es schwierig, direkt aus der Visualisierung, gemeinschaftliche oder hierarchischen Strukturen zu erkennen.
Denn dieser Algorithmus ist in seiner Funktionsweise auf Single Layer Netzwerke ausgerichtet worden, kann jedoch durch Ergänzung weiterer Algorithmen optimiert und für Multilayer Netzwerke anwendbar gemacht werden.

Kamada Kawais Modell

Bei der Überführung in das Modell von Kamada und Kawais wird nicht mehr zwischen anziehenden und abstoßenden Kräften unterschieden. Hier werden die Kanten zwischen zwei Knoten als Federn dargestellt. Ziel ist es, dass sich das System in einem Zustand mit minimal gespannten Federn befindet. Der Graphen theoretisch kürzeste Pfad ist dabei die Grundlänge der Feder (Niggemann & Stein, 2000).
Knoten stoßen sich damit ab oder ziehen sich an, je nachdem, ob die geometrische Entfernung größer oder kleiner als die Graphen theoretische Entfernung ist. Bei diesem Verfahren wird Schritt für Schritt über den Knoten, mit der am größten auf ihn wirkenden Kraft, iteriert und dieser so versetzt, dass diese minimal wird (Kamada et al., 1989). (siehe Abbildung 12)
Die Rechenzeit hängt dabei stark von der Anzahl der Knoten, jedoch nicht von der Anzahl der Kanten ab.

Clustering Algorithmus

Eine weiter Möglichkeit für die Verbesserung des, auf Kräfte basierenden, Fruchterman Reingold Algorithmus wäre es, den einzelnen anziehenden Kräften verschiedene Stärken zuzuweisen. Dabei könnte die Anzahl der gemeinsamen Parameter die Stärke bestimmen.
Dadurch wird die Gewichtung der Knoten, welche sich in gleichen hierarchischen Strukturen befinden, verändert. Dies kann durch ein Clustering Algorithmus berücksichtigt und dient als Maß der Ähnlichkeit zwischen zwei Knoten (Shenhao & Ronghuan, 2021).

Beim Clustering Algorithmus handelt es sich um ein Verfahren, welches Ähnlichkeitsstrukturen in Datenbeständen erkennen soll. Dadurch werden ähnliche Knoten zusammen gruppiert (Likas et al., 2003). Ein passendes Verfahren, um Communities mit ähnlichen Merkmalen in einer solchen Visualisierung direkt zu erkennen. Die Ähnlichkeit wird dabei durch verschiedene Metriken definiert, wie z.B. Studierende, die im gleichen Semester sind und über die gleiche Plattform mit einem weiteren Studierenden verbunden sind.
Dabei werden Knoten verschiedener Ebenen nacheinander geclustert und die mehrschichtige Struktur des Netzes entsprechend der Anzeigeebene dargestellt (Shenhao & Ronghuan, 2021).
Eine Ergänzung wäre noch eine zentrale Kraft, die auf jeden Knoten wirkt, die für die zentrale Platzierung des Layout-Ergebnisses sorgt.
Somit kann die Gemeinschaftsstruktur passender dargestellt werden.
In Abbildung 13 ist zu sehen, dass dadurch Knoten, die durch mehrere Parameter miteinander verbunden sind (wenn mehrere Knotenattribute vorhanden sind), näher beieinander als Knoten, die nur mit einem Parameter verbunden sind.

Visuelle Repräsentation der Anordnungsalgorithmen

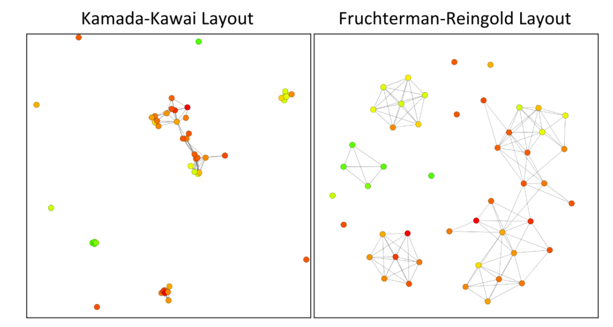Abbildung 12
Hier ist die Repräsentation eines Datensatzes nach dem Fruchterman Reingold Algorithmus und nach dem Kamada Kawais Algorithmus zu sehen. (de León & Bajorath, 2016) Abbildung 13
(a) Zeigt ein eindimensionales Netzwerk nach der Anwendung des Fruchterman-Reingold Algorithmus.
(b) Ein eindimensionales Layout nach der optimierten Methode des Clustering und der Hinzufügung von Kräften.
(c) Zeigt eine Hierarchische Struktur.(Shenhao & Ronghuan, 2021)

Diese Visualisierungen zeigen auf, dass es einen deutlichen Unterschied der Knotenanordnung zwischen dem einfachen Fruchterman Reingold Algorithmus und den optimierten Methoden mit Federn, Clustering und Kraftstärken gibt. Es zeigt, dass die optimierten Methoden die Community-Struktur und die hierarchische Struktur des Multilayer Netzwerks effektiver darstellen kann und den Nutzern hilft, seine strukturellen Merkmale zu verstehen und zu analysieren. Eine Weiterentwicklung der, auf Single Layer ausgelegten Algorithmen, ist also dringend erforderlich.

Kompression

Eine Frage, die sich bei jeglicher Art von Visualisierung stellt, ist die Möglichkeit nach Vereinfachung. Dabei muss entschieden werden, welche Informationen notwendig sind, um die Struktur von mehrschichtigen Netzwerken korrekt darzustellen und ob es realisierbar ist Layer ohne beziehungsweise mit vertretbarem Informationsverlust zusammenzufassen.
Ein zugrunde liegender Konflikt ist dabei die individuelle Definition von “minimaler Informationsverlust”.
Aus diesem Grund bietet MuxViz die Möglichkeit der eigenen Implementation einer Methode zur Komprimierung an. Die bereits in MuxViz implementierte Methode basiert auf der Verwendung von einem, für die Entwickler, optimalen Kompromiss, welcher Komplexität und Informationsgenauigkeit gegeneinander abwägt (Kivelä et al., 2014).

4. Evaluation

Anhand unseres selbst konstruierten Datensatzes und der Visualisierung in den verschiedenen Versionen ist zu erkennen, was die jeweiligen Vor- und Nachteile der Visualisierungsmethoden sind. 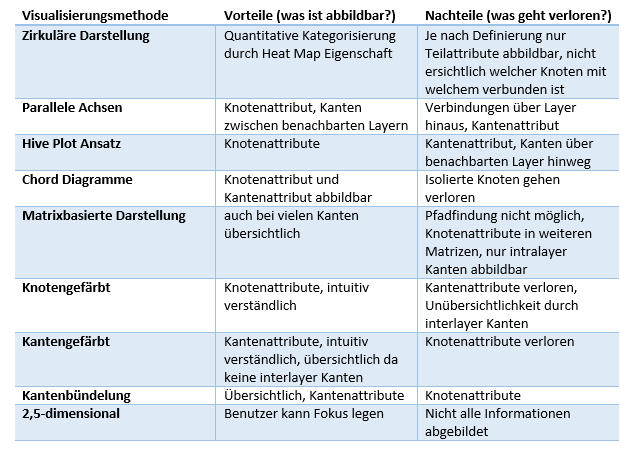Tabelle 2
Vor- und Nachteile der in der Arbeit vorgestellten Darstellungsmöglichkeiten

Die Verwendung von dreidimensionalen Layouts ist in der Forschungsgemeinschaft der Informationsvisualisierung weit weniger verbreitet.
Zwar sind Netze mit mehreren Schichten in der Lage, eine viel detailliertere Beschreibung eines Systems zu kapseln als einschichtige Netze. Jedoch führt diese Visualisierungsmethode zur Herausforderung bei der Datenerfassung, welche in der Anwendung später auch wirklich nutzbar sein sollten.
Obwohl beispielsweise klar ist, dass die Verwendung einer einzigen Art von Kante zwischen einem Paar von Personen nicht immer ein geeignetes Abstraktionsniveau für die Untersuchung sozialer Netzwerke bietet (Wasserman et al., 1994), sind Daten über empirische soziale Netzwerke immer noch hauptsächlich in einem Format verfügbar, das für monoplexe Netzwerke besser geeignet ist als für Multilayer Netzwerke (Kivelä et al., 2014).
Dreidimensionale Layouts dienen so in erster Linie dafür, komplexe Daten auf einen Blick für den Betrachter zu veranschaulichen. Damit ist die Entwicklung vor allem sinnvoll, um das Verständnis der Struktur zu steigern wobei ein geeignetes Abstraktionsniveau zu wählen ist.
In jüngerer Zeit wurden große Multiplex-Datensätze sozialer Netzwerke automatisch erfasst. Die meisten der groß angelegten Multiplex-Netzwerk-Datensätze sind knotenorientiert, das heißt alle Knoten sind in allen Schichten vorhanden (Kivelä et al., 2014). Es gibt jedoch beispielsweise auch einen großen Datensatz, der Beziehungen über mehrere Social-Networking-Sites abdeckt und Schichten liefert, die nicht knotenorientiert sind (Buccafurri et al., 2013).
Ein weithin akzeptierter Ansatz in der Informationsvisualisierung, insbesondere zum Zweck der vergleichenden Analyse von Graphen, besteht deshalb in der Verwendung kleiner Mehrfachansichten.
Softwares wie MuxViz arbeiten somit daran Multilayer Netzwerke zu analysieren und gekonnt zu visualisieren.

5. Zusammenfassung

Zusammenfassend lässt sich sagen, dass sich die Visualisierungsmethoden von Multilayer Netzwerken vor allem in Zwei- und dreidimensionale Arten kategorisieren lassen. Basieren tun dabei die meisten Ansätze auf der graphischen Abbildung von Singlelayer Netzwerken, welche auf das Konzept von Layers erweitert werden. Welche Darstellungsart sich am besten eignet ist pauschal nicht zu beantworten. Relevant sind dafür immer Kontext, auf welchen Aspekten der Fokus liegen soll, was man aus dieser Visualisierung genau erkennen soll, und die Informationsdichte der zugrunde liegenden Daten.

Die Zweidimensionale Darstellung unternimmt den Versuch komplexe Informationen zu vereinfachen, was zu einem Informationsverlusst führt, weshalb man zum Beispiel abwägen muss, ob das Auslassen isolierter Knoten zu sehr die Analyse beeinflusst oder nicht.
Die Dreidimensionale Darstellung bietet eine deutlich intuitivere und übersichtlichere Ansicht auf einen Datensatz. Sie kann dabei auch durch den interaktiven 2,5-dimensionale Ansatz, das Problem von Kantenüberschneidungen vermeiden.

Ein wichtiger Bestandteil bei der Visualisierung ist, welcher Algorithmus zur Platzierung der Knoten verwendet wird. Dargelegt wurde in diesem Paper der Ansatz des kräfteorientierten Layouts und zwei Wege dieses, in Bezug auf Multilayer Netzwerke, zu Optimieren. Dies geschieht mit dem Ziel die graphische Darstellung ästhetisch und verständlich zu formatieren.
Auch unser verwendetes Praxisbeispiel MuxViz kombiniert zwei Kräftebasierte Algorithmen.

Es gibt noch viele weitere Ansätze, um die Visualisierung von Multilayer Netzwerken zu vereinfachen beziehungsweise überhaupt zu ermöglichen. Dazu gehört auch die Zusammensetzung mehrerer Visualisierungsmethoden um das Optimum zu finden.
Da die Daten und Beziehungen in sozialen Netzwerken mit der Zeit vermutlich deutlich komplexer und umfangreicher werden, wird eine Optimierung der Visualisierungsmethoden dringend notwendig sein. Jedoch ist dabei die Vermeidung von Informationsverlust und das Weiterentwickeln, der auf Single Layer basierenden, Algorithmen notwendig um die mathematische Grundlage zu schaffen.

6. Referenzen

1. Mcgee, F., Ghoniem, M., Melançon, G., Otjacques, B., & Pinaud, B. (2019). The state of the art in multilayer network visualization. Computer Graphics Forum, 38(6), 125–149.
2. Kivelä, M., Arenas, A., Barthelemy, M., Gleeson, J. P., Moreno, Y., & Porter, M. A. (2014). Multilayer networks. Journal of Complex Networks, 2(3), 203–271.
3. Manlio De Domenico, A. A., Mason A. Porter. (2015). MuxViz: a tool for multilayer analysis and visualization of networks. Journal of Complex Networks, 3(2), 159–176. https://doi.org/10.1093/comnet/cnu038
4. Shenhao, A., & Ronghuan, Y. (2021). Multi-Layer Network Visualization Based on Force-Directed Algorithm. 2021 2nd International Conference on Artificial Intelligence and Information Systems. https://doi.org/10.1145/3469213.3470410
5. Bothorel, G., Serrurier, M., & Hurter, C. (2013). Visualization of frequent itemsets with nested circular layout and bundling algorithm. International Symposium on Visual Computing, 396–405.
6. Ghani, S., Kwon, B. C., Lee, S., Yi, J. S., & Elmqvist, N. (2013). Visual analytics for multimodal social network analysis: A design study with social scientists. IEEE Transactions on Visualization and Computer Graphics, 19(12), 2032–2041.
7. Krzywinski, M., Birol, I., Jones, S. J. M., & Marra, M. A. (2012). Hive plots—rational approach to visualizing networks. Briefings in Bioinformatics, 13(5), 627–644.
8. Jalali, A. (2016). Supporting social network analysis using chord diagram in process mining. International Conference on Business Informatics Research, 16–32.
9. Bianconi, G. (2018). Multilayer networks: structure and function. Oxford university press.
10. Hammoud, Z., & Kramer, F. (2020). Multilayer networks: aspects, implementations, and application in biomedicine. Big Data Analytics, 5(1), 1–18.
11. Berlingerio, M., Coscia, M., Giannotti, F., Monreale, A., & Pedreschi, D. (2011). Foundations of Multidimensional Network Analysis. 2011 International Conference on Advances in Social Networks Analysis and Mining, 485–489. https://doi.org/10.1109/ASONAM.2011.103
12. Davis, D., Lichtenwalter, R., & Chawla, N. V. (2011). Multi-relational link prediction in heterogeneous information networks. 2011 International Conference on Advances in Social Networks Analysis and Mining, 281–288.
13. Henry, N., Fekete, J.-D., & McGuffin, M. J. (2007). NodeTrix: a hybrid visualization of social networks. IEEE Transactions on Visualization and Computer Graphics, 13(6), 1302–1309.
14. Neef, D. (2009). Automatisches Layout für Produktfunktionsdarstellung im CAD-Umfeld [Master's thesis]. Hochschule Mittweida.
15. Thomas M. J. Fruchterman, E. M. R. (1991). Graph drawing by force-directed placement. Software: Practice and Experience, 21(11), 1129–1164. https://doi.org/10.1002/spe.4380211102
16. Niggemann, O., & Stein, B. (2000). Meta heuristic for graph drawing. Learning the optimal graph-drawing method for clustered graphs. 286–289. https://doi.org/10.1145/345513.345354
17. Kamada, T., Kawai, S., & others. (1989). An algorithm for drawing general undirected graphs. Information Processing Letters, 31(1), 7–15.
18. Likas, A., Vlassis, N., & Verbeek, J. J. (2003). The global k-means clustering algorithm. Pattern Recognition, 36(2), 451–461.
19. de León, A. de la V., & Bajorath, J. (2016). Design of chemical space networks incorporating compound distance relationships. F1000Research, 5.
20. Wasserman, S., Faust, K., & others. (1994). Social network analysis: Methods and applications.
21. Buccafurri, F., Foti, V. D., Lax, G., Nocera, A., & Ursino, D. (2013). Bridge analysis in a social internetworking scenario. Information Sciences, 224, 1–18.