Anwendung des Borgia Clustering
| Konrad Schindler | Jonas Säuberlich | ||
|---|---|---|---|
| RWTH Aachen University | RWTH Aachen University | ||
| konrad.schindler@rwth-aachen.de | jonas.saeuberlich@rwth-aachen.de |
Abstract
In dieser Arbeit wird ein Überblick über das Borgia Clustering, einem neuen Algorithmus zur Gemeinschaftserkennung auf Netzwerken, gegeben. Dem Algorithmus liegen einzigartige Ideen zugrunde. Dazu zählt das Prinzip der Gravitation, welches ursprünglich aus dem Fachgebiet der Physik stammt. Diese neue Grundlage des Algorithmus ist dafür verantwortlich, dass andere Probleme auftauchen, als bei anderen Algorithmen. Der Algorithmus kann beispielsweise die speziellen Eigenschaften eines vorzeichenbehafteten Netzwerks nicht berücksichtigen. Es wird anhand kürzlich erfassten Abstimmungsergebnisse des Europäischen Parlaments mit Hilfe eines geeigneten Algorithmus gezeigt, dass diese Eigenschaften ausschlaggebend für eine sinnvolle Analyse sind. Daraus wird geschlossen, dass vorzeichenbehaftete Netzwerke kein Anwendungsfeld des Borgia Clusterings - in seiner momentanen Form - darstellen.
Inhaltsverzeichnis
Einleitung
In vielen Netzwerken sind Akteure Mitglied von mehr als nur einer Gemeinschaft. Ein prominentes Beispiel dafür ist reddit.com. Ein Nutzer kann sich beispielsweise gleichzeitig über die nächste große Kryptowährung in r/CryptoCurrency diskutieren, Katzenbilder in r/aww anschauen und sich über seine Sexualität in r/lgbtq austauschen. Auch soziale Gruppen überschneiden sich. Eine Person kann einer Familie, einem Freundeskreis, verschiedenen Vereinen, einem Kollegenkreis etc. angehören. Darüber hinaus spielen überlappende Gemeinschaften auch in biologischen Netzwerken eine wichtige Rolle (Xie et al., 2013), wie es bereits von Hyun Kim und Hyejin Kang in ihrer Arbeit (Kim & Kang, 2020) dargestellt wurde.
Dargestellt werden solche Netzwerke durch Graphen, wobei Akteure die Rolle der Knoten und die Beziehungen die der Kanten übernehmen. Zusätzlich wird zwischen vorzeichenbehafteten und vorzeichenlosen Netzwerken unterschieden. In dieser Ausarbeitung wird sich mit der Anwendung auf vorzeichenbehaftete Netzwerke konzentriert. Das bedeutet, dass Netzwerke negative Beziehungen beinhalten und dementsprechend Algorithmen verwendet werden müssen, die solche negativen Beziehungen berücksichtigen. Genauer beschäftigt sich diese Arbeit mit dem Borgia Clustering und dessen Platz innerhalb von „Overlapping Community Detection Algorithms” (im Folgenden OCDA genannt) für vorzeichenbehaftete Netzwerke.
Das Borgia Clustering wählt einen intuitiveren Ansatz, als andere Algorithmen es tun würden, um das Netzwerk in Gemeinschaften zu teilen. Dabei werden Akteuren ähnliche Attribute zugewiesen, wie sie bei Objekten in einem Gravitationssystem zu finden sind. Beispielsweise wirken Akteure mit hohem sozialem Einfluss - vergleichbar zu massereichen Objekten - eine starke Anziehungskraft auf andere Akteure aus. Insbesondere wird in der Arbeit darauf eingegangen, wie die Adaption, eines anwendungsfremden Algorithmus, der des „Gravitational Clustering” vor sich geht, damit neue Funktionalitäten erschlossen werden können.
Weiter wird sich damit beschäftigt den resultierenden Algorithmus, das Borgia Clustering, als OCDA auf vorzeichenbehafteten Netzwerken zu testen. Da der Algorithmus keine Möglichkeit zur Erkennung von überlappenden Gemeinschaften hat und nicht für vorzeichenbehaftete Netzwerke entwickelt wurde, prüft die Arbeit inwieweit diese Eigenschaften ausschlaggebend für ein aussagekräftiges Resultat sind. Dazu wird die Anwendung von OCDA in politischen Konstrukten analysiert. Genauer wird der Signed DMID Algorithmus von (Shahriari & Klamma, 8252015) auf das Abstimmungsverhalten der Abgeordneten im Europäischen Parlament angewendet.
Zu Beginn werden die Grundlagen des Borgia Clustering, unter anderem das Gravitational Clustering, vorgestellt. Darauf folgt die Erläuterung des Borgia Clustering und wie es die vorher genannten Funktionen adoptiert, um daraus einen Algorithmus zur Gemeinschaftserkennung zu machen. Nach der Erläuterung befasst sich die Arbeit mit der bisherigen Anwendung des Borgia Clustering und den Problemen, die sich bei der Anwendung auf vorzeichenbehafteten Netzwerken ergeben. Zum Schluss wird mithilfe einer vollständigen OCDA Analyse eines Netzwerks gezeigt, weshalb das Borgia Clustering zu stark eingeschränkt ist, um vergleichbare Resultate zu liefern.
Verwandte Arbeiten
Einen allgemeinen Überblick über das Thema Overlapping Community Detection und den Einsatz von Algorithmen für selbige gibt der Autor von „Overlapping community detection in networks“ (Xie et al., 2013). Das Paper beschäftigt sich mit verschiedensten Algorithmen, Qualtitätsmaßen und dem Benchmarken der Algorithmen. Als Grundlage für die Ausarbeitung stehen zwei Arbeiten Modell. Zunächst erläutert und entwirft W.E. Wright in „Gravitational Clustering“ (Wright, 1977) die Grundlage für Algorithmen, welche sich das physikalische System der Gravitation zunutze machen. Als weitere essentielle Arbeit ist auch die Arbeit von Fumanal-Idocin et al. „Community detection and Social Network analysis based on the Italian wars of 15th century“ (Fumanal-Idocin et al., 2020) zu nennen. Hier wurde das Borgia Clustering entwickelt und angewendet. Eine Anwendung von OCDAs auf die politische Überschneidung der Anhänger einer Partei wird in Politische und Ökonomische Netzwerke von David Schliewe und Fabian Gries (Schliewe & Gries, 2020) anhand der Twitter-Follower politischer Mandatsträger analysiert. Hier wurde untersucht, in wie weit sich die Anhänger von Politikern mit anderen Politikern überschneiden und inwiefern die daraus entstehenden Gemeinschaften mit den realen Parteien übereinstimmen.
Im Gegensatz zu diesen Arbeiten wurde sich in dieser Arbeit auf die Unterschiede vom Gravitational Clustering und dem Borgia Clustering, sowie den dafür notwendigen Aktualisierungen konzentriert. Hinzukommend wird die Zugehörigkeit von politischen Abgeordneten zu Gemeinschaften nicht durch deren Follower bestimmt, sondern durch das persönliche Abstimmungsverhalten.
Methodik
Im Folgenden wird das Borgia Clustering vorgestellt. Als dessen Grundlage, wird allerdings zunächst das Gravitational Clustering erläutert werden. Die geringere Abstraktion des Gravitational Clustering hilft außerdem beim späteren Verständnis. Als eine weitere Basis für die Funktionalität vom Borgia Clustering werden Affinity Functions vorgestellt. Dabei handelt es sich um Funktionen zur Modellierung von Beziehungen zwischen Akteuren in Netzwerken. Diese ermöglichen es mit dem Borgia Clustering Gruppierungsprozesse ähnlich zu menschlichen Interaktionen zu implementieren.
Gravitational Algorithm
Der grundlegende Algorithmus und die Voraussetzung des Borgia Clustering ist für das Gruppieren von Daten entwickelt worden. Es handelt sich bei dem Gravitational Clustering um eine Technik, welche mithilfe des physikalischen Prinzips der Gravitation, Daten analysiert. Nicht-masselose Teilchen in einem Gravitationssystem bewegen sich abhängig von deren Position und dem Gewicht der Teilchen auf einander zu. Es wirkt eine Gravitationskraft zwischen den Teilchen. Hierbei ist es irrelevant, dass die Teilchen eine Initialgeschwindigkeit von 0 besitzen. Zwei Teilchen kollidieren zu einem Cluster, wenn sie einen gemeinsamen Schwerpunkt erreicht haben und sich somit nicht weiter aufeinander zu bewegen können. Da sich alle Teilchen gegenseitig anziehen und nicht abstoßen entwickelt sich das System dahingehend, dass es mit der Zeit immer weniger, aber massereichere Teilchen gibt. Der Algorithmus terminiert, wenn lediglich ein Cluster mit der kombinierten Masse aller Teilchen übrig bleibt.
Dieses Phänomen simuliert Wright in seinem Algorithmus, um Teilchen auf Cluster aufzuteilen. Jedes Teilchen stellt initial genau ein Cluster dar. Verbinden sich zwei Teilchen, werden die zugehörigen Cluster vereinigt und formen ein kombiniertes neues Cluster. Der Zustand des Systems mit genau k Teilchen beschreibt die optimale Verteilung auf k Cluster. Befindet sich das System beispielsweise in einem Zustand mit nur noch zwei Teilchen, ist dies die optimale Verteilung aller Teilchen aufgeteilt auf zwei Cluster. Um eine passende Clusterverteilung für Daten finden zu können, wird die stabilste Verteilung berechnet. Das heißt, es wird der Zustand gewählt wird, in dem die Anzahl der Cluster am längsten gleich bleibt. Beispielsweise existieren in einem Ursprungszustand 100 Teilchen. Es wird angenommen, dass zu Beginn viele Teilchen verschmelzen, so dass nach zehn Sekunden lediglich noch fünf Cluster bestehen. Nach 50 weiteren Sekunden verbinden sich die noch bestehenden Cluster zu zwei Cluster. Der finale Zustand mit nur noch einem Teilchen wird in den folgenden 40 Sekunden erreicht. Dementsprechend überdauerte der Zustand mit fünf Teilchen 50% der gesamten simulierten Zeit und wird folglich von dem Algorithmus als bester Zustand berechnet.
Für ein besseres und detailieres Verständnis gibt die folgende Auflistung der Berechnungsschritte des Algorithmus einen Überblick:
- n Teilchen werden mit ihren Positionsvektoren \(s_1,...,s_n\) und ihren Massen \(m_1,...,m_n\) initialisiert.
- Wählen der maximale Entfernung \(\delta\), um welche sich das schnellste Teilchen in jeder Iteration bewegen darf
- Bestimmung des Radius \(\varepsilon\), ab wann zwei Teilchen zu einem Cluster verschmelzen.
- Begonnen wird mit der Zeit \(t = 0\).
- Wiederholen der Schritte 6. - 9. bis nur noch ein Teilchen über bleibt.
- Berechnung der Bewegung \(g(k, t, dt)\) für jedes Teilchen \(k\) im Intervall \([t, t + dt]\), wobei \(dt\) die Zeit ist, die das schnellste Teilchen benötigt, um sich um \(\delta\) zu bewegen.
- Aktualisierung der Position jedes Teilchens. Berechnet mithilfe von \(s_k(t+dt) = s_k(t) + g(k, t, dt)\). Die Berechnung folgt nach dem Algorithmus.
- Setze \(t = t + dt\).
- Überprüfung des Abstandes zwischen allen Teilchenpaaren \((i, j)\). Ist der Abstand kleiner als \(\varepsilon\) verschmelzen die Teilchen zu einem geeinten Cluster \(k\) mit der Masse \(m_k = m_i + m_j\) und der Position \(s_k = \frac{m_i s_i + m_j s_j}{m_i + m_j}\).
- Bestimmung des stabilsten Zustandes
Die Berechnung der Bewegung funktioniert mithilfe der Formel \(g(k,t,dt)\), wobei \(N(t)\) der Anzahl der Teilchen zum Zeitpunkt \(t\) entspricht und \(p\) und \(q\) dazu dienen um unterschiedliche Modelle zu simulieren.
Wie in der Formel zu sehen ist, ist die Geschwindigkeit der Teilchen irrelevant für die Berechnung der Teilchen. Es wird lediglich durch eine Berechnung aus den Massen und den Positionen aller Cluster eine aktualisierte Position berechnet. Als Folge werden Teilchen, anders als in physikalischen Gravitationsmodellen, nicht einander umkreisen oder oszillieren.
Video 1: Visualisierung des Algorithmus (Robin De Baets, 2020)
Affinity Functions
Alle Akteure in einem Netzwerk stehen zueinander in einer Beziehung. Diese Beziehungen werden Affinitäten genannt. Diese Zuneigungen können im Borgia Clustering anhand verschiedener Kriterien berechnet werden. Für alle Affinitäten gilt, dass sie gerichtet sind und sie zwischen genau zwei Akteuren stattfinden. Es gibt eingehende und ausgehende Affinitäten, welche jedoch gleich berechnet werden. Im Allgemeinen wird zwischen persönlichen und strukturellen Affinitäten unterschieden. Während die persönlichen Affinitäten die direkte Beziehung zwischen den Akteuren darstellen, betrachten strukturelle Affinitäten die Umgebung der zwei Akteure. In den vom Borgia Clustering verwendeten Affinitäten handelt es sich, mit Ausnahme von der Machiavelli Affinität, um persönliche Affinitäten. Die Berechnung der Affinitäten beruht auf direkten, bereits existierenden Kantengewichten in einem gerichteten Graphen. Die Adjazenzmatrix wird mit \(C\) und die Anzahl der Knoten mit \(N\) bezeichnet.
Bester Freund
Bei dieser Affinität wird berechnet, wie wichtig jeder andere Akteur prozentual für das Gesamtbild der Beziehungen vom betrachteten Akteur sind.
\[A_C(x,y) = \frac{C_{x,y}}{\sum^N_{a=1}C_{x,a}}\]Bester gemeinsamer Freund
Im Gegensatz zu der vorherigen Affinität wird hier nicht nur die direkte Beziehung zwischen zwei Akteuren betrachtet, sondern auch die Beziehung zu gemeinsamen Nachbarn. Es wird überprüft, welcher Akteur das beste Verhältnis mit beiden Akteuren hat. Hierfür wird immer die schlechtere Beziehung der beiden Akteure zu dem Dritten betrachtet.
\[A_C(x,y) = \frac{Max\{Min(C_{x,z},C_{y,z})\}}{\sum^N_{a=1}C_{x,a}}\]Freunde für immer
Ergänzend zu der Affinität bester Freund kommt ein Faktor der Zeit hinzu. Beziehungen werden belohnt, wenn sie über eine lange Zeitperiode eine gute Beziehung zu einem anderen Akteur pflegen.
\[A_C(x,y) = \frac{1}{|T|}\sum_{t \in T}(\frac{C_{x,y}(t)}{\sum^N_{a=1}C_{x,a}(t)})\]Soziale Vernetzung
Ähnlich zu der Affinität bester gemeinsamer Freund wird diese Beziehung aufgrund des Umfeldes der Akteure bestimmt. Es wird der Mittelwert aus den Beziehungen von dem Umfeld des Akteurs 1 zu dem Akteur 2 berechnet.
\[A_C(x,y) = Mean(A'_C(x',y))\quad \forall x',so\; dass\; A'_C(x,x') > 0\]Machiavelli
Bei dieser strukturellen Affinität wird die Ähnlichkeit der strukturellen Relevanz berechnet. Je ähnlicher in ihrem sozialen Status sind, desto höher ist der berechnete Wert.
\[A_C(x,y) = 1 - \frac{abs(I_x-I_y)}{Max(I_x,I_y)}, \quad I_a = Sum(Degree(x'))\; \forall a, so\; dass\; C(a,x') > 0\]Borgia Clustering
Ein Grundprinzip des Borgia Clustering ist es, dass reale zwischenmenschliche Interaktionen und deren Funktionsweisen angewendet werden um Communities zu gruppieren. Als Grundlage für den Algorithmus wurde zum einen die Funktionsweise des Gravitational Clustering auf Communities angewandt, als auch die menschlichen und machtpolitischen Interaktionen. Ableitend daraus stammt der Name von dem italienischen Politiker Cesare Borgia, welcher eine wichtige Rolle in den italienischen Kriegen im 15. Jahrhundert gespielt hat.
(Fumanal-Idocin et al., 2020) stellen Grundannahmen auf, welche sowohl für reale Staaten und konkurrierende Parteien in der Renaissance, als auch für moderne Communities gelten:
- Alle Länder und Communities wollen wachsen. Sie wollen einen größeren Einfluss gewinnen.
- Einige Staaten/Communities haben mehr gemeinsam und sind ähnlicher zu einander als zu anderen. Bei realen Staaten handelt es sich hierbei um Ähnlichkeiten in der Kultur oder durch die geographische Lage. Bei Communities wird dies mithilfe von Initialbeziehungen oder Affinitäten modelliert.
- Für Staaten gilt, Allianzen oder Verbindungen mit mächtigen und einflussreichen Ländern haben eine größeren Einfluss als mit schwächeren Partein. Auf Netzwerke übertragen bedeutet es, dass Akteure stärker von sozial relevanten Communities angezogen werden, als von unbedeutenden.
- Die schiere Größe ist nicht allein bedeutend für die Anziehungskraft und Relevanz von Staaten und Communities. Eine weitere wichtige Rolle spielen beispielsweise die Ausgangslage oder wie sich weitere Akteure verhalten.
Mit diesen Grundannahmen gibt es einige Punkte, in welchen sich das Borgia Clustering von dem Gravitational Clustering unterscheidet. Der Algorithmus des Gravitational Clusterings muss also aktualisiert werden.
Zunächst werden keine Teilchen mehr verwendet, sondern Akteure. Diese speichern nicht mehr eine Position und ein Gewicht, sondern Informationen, die innerhalb eines Netzwerks relevant sind. Die Masse der simpleren Teilchen wird durch den sozialen Wert \(m\) ersetzt. Initial ist dieser Wert mit der Anzahl der Verbindungen, also dem Grad des Akteurs, gleichzusetzen. In der Anwendung heißt das, je vernetzter ein Knoten ist, desto höher ist dessen soziale Relevanz. Weiterhin wird die Position der Teilchen durch einen Einfluss ersetzt. Resultierend wird die Positionsmatrix durch eine Einflussmatrix \(S\) ausgetauscht. Hinzukommend existiert eine neue Matrix für die Affinitäten \(A_C\) zwischen allen Knoten. Die initiale Matrix \(S\) wird gleich der Affinitätenmatrix \(A_C\) gesetzt.
Ergänzend zum sozialen Wert - dem „Gewicht“ - definiert sich die Anziehungskraft zwischen zwei Akteuren auch über deren Einfluss - der „Distanz“. Um zu modellieren, dass größere Communities immobiler sind als kleine, wird ein „greedy expanse“ Malus mit dem Parameter \(p\) eingeführt. Der Malus wird berechnet mithilfe \(\frac{1}{m^p_x}\), wobei \(p\) der gewählte Parameter ist und \(m_x\) der soziale Wert des Knotens ist. Mithilfe einer T-Norm Funktion, die bspw. in (Gupta & Qi, 1991) erläutert werden, wird die Laufzeit optimiert. Daraus resultiert die folgende Funktion um die Anziehungskraft zwischen zwei Akteuren zu berechnen:
\[F_{xy}=\frac{T((m_xm_y)^c,A_c(x,y))}{m^p_x}\cdot\frac{s_x-s_y}{|s_x-s_y|^3}dt\]Hinzukommend wird die maximale Bewegung der Akteure, wie auch beim Gravitational Clustering, durch den Parameter \(\delta\) beschränkt. Herausgehend wird die Bewegung der anderen Knoten im Vergleich mit dem schnellsten Knotens mithilfe von \(dt\) berechnet. Wie bereits bekannt, handelt es sich bei \(dt\) um die Länge des Zeitintervalls, welches betrachtet wird.
Nachdem die Berechnung der Anziehungskraft abgeschlossen ist, spielt die Kollision von zwei Akteuren eine zentrale Rolle. Wenn zwei Akteure kollidieren, verschmelzen sie miteinander. Im Gegensatz zum klassischen Gravitational Clustering wird hier nicht die euklidische Distanz der Teilchen betrachtet, sondern der soziale Einfluss, welche die Teilchen über einander haben. Zwei Akteure verschmelzen genau dann, wenn der Einfluss, den Akteur A über B größer ist als der Einfluss, den Akteur B über sich selber hat. Es muss also \(S(a,b)> S(b,b)\) gelten.
Die Berechnung des sozialen Wertes des neuen Akteurs funktioniert durch die simple Addition der sozialen Werte von A und B: \(m_a + m_b\). Weiterhin ist die neue Position und damit die sozialen Einflüsse der Mittelpunkt der ursprünglichen Einflüsse \(s_a\) und \(s_b\). Die daraus folgenden Affinitäten sind:
\[A_C(ab)=\frac{m_aA_C+m_bA_C(b)}{m_a+m_b}\]Der Algorithmus ähnelt im Kern dem des Gravitational Clusterings. Zunächst wird mithilfe der folgenden Funktion die Bewegung jedes Knotens berechnet:
\[g_i(t)=\frac{1}{m_i^p}\sum_{j\neq i}T((m_im_j)^c,A_C(i,j))\frac{s_j(t)-s_i(t)}{|s_j(t)-s_i(t)|^3}dt\]
Für den schnellsten Akteur \(F\) wird \(dt(t)\) für den nächsten Schritt berechnet, wobei \(\delta =|g_F(t)|\) ist:
Anschließend wird der Einfluss für jeden Akteur i auf
\[s_i(t+dt(t))=s_i(t)+\frac{g_i(t)}{m_i}\]gesetzt und \(t\) wird durch \(t+dt(t)\) ersetzt. Nun wird überprüft, ob Akteure kollidieren. Falls das der Fall ist, formen sie einen neuen Knoten. Falls nur noch ein Akteur übrig ist, wird das Programm beendet, ansonsten werden die Schritte wiederholt.
Ein großer Nachteil vom herkömmlichen Gravitational Clustering ist, dass die stabilste Konfiguration in den meisten Fällen eine ist, wo nur noch sehr wenige Knoten existieren. Für das Borgia Clustering ist dies jedoch nicht wünschenswert. Stattdessen werden die Konfigurationen nicht nur durch die Zeit bewertet, sondern auch wie viele Gemeinschaften noch existieren. Hierbei gilt, sowohl Stabilität, als auch Größe werden belohnt. Berechnet wird dies mithilfe von:
\[R(Z)=SimulatedTime(Z)\cdot log(NumCommunities(Z))\]Abschließend wird der Algorithmus noch von Parametern beeinflusst, welche zuvor eingegeben werden. Zunächst ist es von Relevanz, welche der bereits vorgestellten Affinitätsfunktionen benutzt werden. Es kann durch die Selektion einer Funktion oder durch Kombinationen der Funktionen verschiedene Verhaltensmuster der Analyse hervorgerufen werden. Beispielsweise kann die Kombination von zwei Affinitäten so aussehen:
\[A_c(x,y)=\alpha \text{Aff1}_c(x,y)+(1-\alpha )\text{Aff2}_C(x,y)\]wobei \(\alpha\) ein frei wählbarer Parameter im Intervall \([0,1]\) ist und Aff1 und Aff2 zwei beliebige Affinitätsfunktionen sind.
Ein Vorteil des Borgia-Clusterings ist, dass im Vergleich zu anderen Algorithmen es nicht notwendig ist, den Algorithmus mehrmals auszuführen, da bei derselben Parameterwahl und derselben Datenmenge es immer in das gleiche Ergebnis resultiert.
Anwendung
Das Konzept des Borgia Clustering wurde zum jetzigen Standpunkt lediglich von den Autoren der Arbeit (Fumanal-Idocin et al., 2020) angewendet. Diese haben den Algorithmus ausführlich für die Analyse von literarischen Texten, wie bspw. „Game of Thrones“ genutzt. Außerdem hat das Borgia Clustering Anwendung auf den Abstimmungsergebnisse des Eurovision Song Contest und dem für Community Detection bekannten Datensatz „Zachary’s Karate Club“ gefunden. Eine detaillierte Auswertung dazu findet sich in der oben genannten Arbeit. Durch diese erfolgreichen Anwendungsbeispiele, steht es außer Frage, dass das Borgia Clustering auch in weiteren Datenmengen zur Gemeinschaftserkennung angewendet werden kann.
Nach der Leitfrage wird nun untersucht, inwieweit eine Anwendung des Algorithmus auf vorzeichenbehaftete Netzwerke möglich ist. Insbesondere wird dies am Beispiel des Abstimmungsverhaltens im Europäischen Parlament durchgeführt.
Problematik
Da das Borgia Clustering auf dem Gravitationsalgorithmus aufgebaut ist und es sich bei negativen Vorzeichen um entgegengesetzte Kräfte handelt, ist es möglich, dass der Algorithmus niemals den finalen Zustand erreicht. Also den Zustand, wo es nur noch einen Akteur gibt. Ein Beispiel, welches im Folgenden betrachtet wird, sind Abstimmungsergebnisse in einem Parlament. Die Kantengewichte in dem Netzwerk stellen die Ähnlichkeit der Abstimmungen der Abgeordneten (Knoten) dar. Dabei bedeutet ein hohes positives bzw. negatives Gewicht, dass die Abgeordneten sehr ähnlich bzw. fast ausschließlich gegensätzlich abstimmen. Eine zu überprüfende These ist die Folgende: Zwei Knoten, die Abgeordnete derselben Partei darstellen tendieren dazu über eine Kante verbunden zu sein, welche ein hohes positives Gewicht besitzen. Die Verbindung zwischen Abgeordneten zweier Parteien, die sich politisch gegenüberstehen, sollte dazu neigen ein negatives Gewicht zu haben. Im Borgia Clustering würde dies nun dazu führen, dass sich Abgeordnete einer Partei zu einem Akteur zusammenschließen. Nach dem Zusammenschluss zu den Partei-Akteuren ist es gut möglich, dass nun der oben genannte Fall eintritt, in dem sich die Akteure im physikalischen Sinne voneinander abstoßen und der Algorithmus somit nie terminiert.
Eine Terminierung ist erzwingbar, indem eine gewünschte Anzahl an Clustern festgelegt wird und der Algorithmus so lange laufen gelassen wird, bis die Anzahl der Akteure damit übereinstimmt. Da man im Voraus jedoch nicht sagen kann, mit welcher Anzahl von Akteuren das Borgia Clustering den Zustand erreichen wird, in dem eine Fusionierung der Akteure nicht mehr stattfindet, kann man diese Angabe nicht viel mehr als raten. Eine andere mögliche Lösung wäre die Festlegung der maximalen Anzahl von Iterationsschritten in einem Zustand. Dabei besteht jedoch die Möglichkeit den Algorithmus zu unterbrechen, während sich Akteure noch immer aufeinander zu bewegen, sollte die Anziehungen zwischen den beiden sehr niedrig sein.
Ein vielversprechenderer Ansatz wäre genau dann zu terminieren, wenn die Bewegung aller Knoten in eine größere Distanz zwischen den Knoten resultiert. Das bedeutet, der Algorithmus terminiert, wenn es keine Annäherung durch eine Bewegung mehr gibt.
Ein weiteres Problem des Algorithmus ist, dass es sich bei dem Resultat nicht um überlappende Gemeinschaften handelt. Akteure fusionieren immer vollständig mit anderen Akteuren. Das bedeutet, dass ein Akteur nicht Teil von zwei Gemeinschaften im Endresultat sein kann. Einen Akteur mehreren Gemeinschaften zuordnen zu können ist jedoch sehr wünschenswert, wie (Reid et al., 2013) zeigt. Dies wird auch im folgenden Experiment gezeigt.
Experiment
Um die Relevanz von OCDA an einem Praxisbeispiel vorzuführen, wurde die oben genannte Idee umgesetzt. Aus dem Abstimmungsverhalten der Abgeordneten des Europäischen Parlaments wurde ein Graph erstellt, auf den der Signed DMID Algorithmus angewendet wurde. (Shahriari & Klamma, 8252015). Bei diesem Algorithmus handelt es sich um eine andere Vorgehensweise, jedoch ist dieser für vorzeichenbehaftete Netzwerke entwickelt worden und wird somit aussagekräftige Resultate liefern. Insgesamt wurden die letzten 2984 Abstimmungen evaluiert (Stand 08.05.2021). Die Abstimmungsergebnisse stehen auf der Seite des Europaparlaments frei zur Verfügung (European Parliament, 2021). Wenn Abgeordnete gleich bzw. unterschiedlich abgestimmt haben bekommen sie für die Abstimmung eine Beziehung von 1 bzw. -1. Das Kantengewicht berechnet sich aus dem Durchschnitt der Beziehungen aller Abstimmungen.
Beispiel
A stimmt FÜR, GEGEN, GEGEN, FÜR, GEGEN, FÜR, FÜR
B stimmt FÜR, GEGEN, FÜR, FÜR, FÜR, GEGEN, GEGEN
dann ist das Kantengewicht:
Zusätzlich wurden alle Kantengewichte um den Durchschnitt reduziert, sodass eine allgemeine Übereinstimmung der großen Mehrheit in einigen Abstimmungen weniger als positive Verbindung gewertet wird. Außerdem wurden Kanten deren Kantengewicht in einem bestimmten Abstand zu Null sind ausgeschlossen, um Rechenaufwand zu verringern und einen übersichtlicheren Graphen zu erhalten. Jede überbleibende Kante hat also ein gewisses Maß an Bedeutung. Entweder stellen sie eindeutig gute oder schlechte Beziehungen dar. Die Daten und Skripte zur Auswertung befinden sich in diesem Git-Repository.
Das Ergebnis:
 Abbildung 1: Das Resultat des Signed DMID Algorithmus angewendet auf das Netzwerk, das das Europäsche Parlament modelliert. Geordnet nach Fraktionen und ihren Sitzplätzen im Parlament, beginnend mit der orangestichigen Fraktion unten links (GUE/NGL).
Abbildung 1: Das Resultat des Signed DMID Algorithmus angewendet auf das Netzwerk, das das Europäsche Parlament modelliert. Geordnet nach Fraktionen und ihren Sitzplätzen im Parlament, beginnend mit der orangestichigen Fraktion unten links (GUE/NGL).
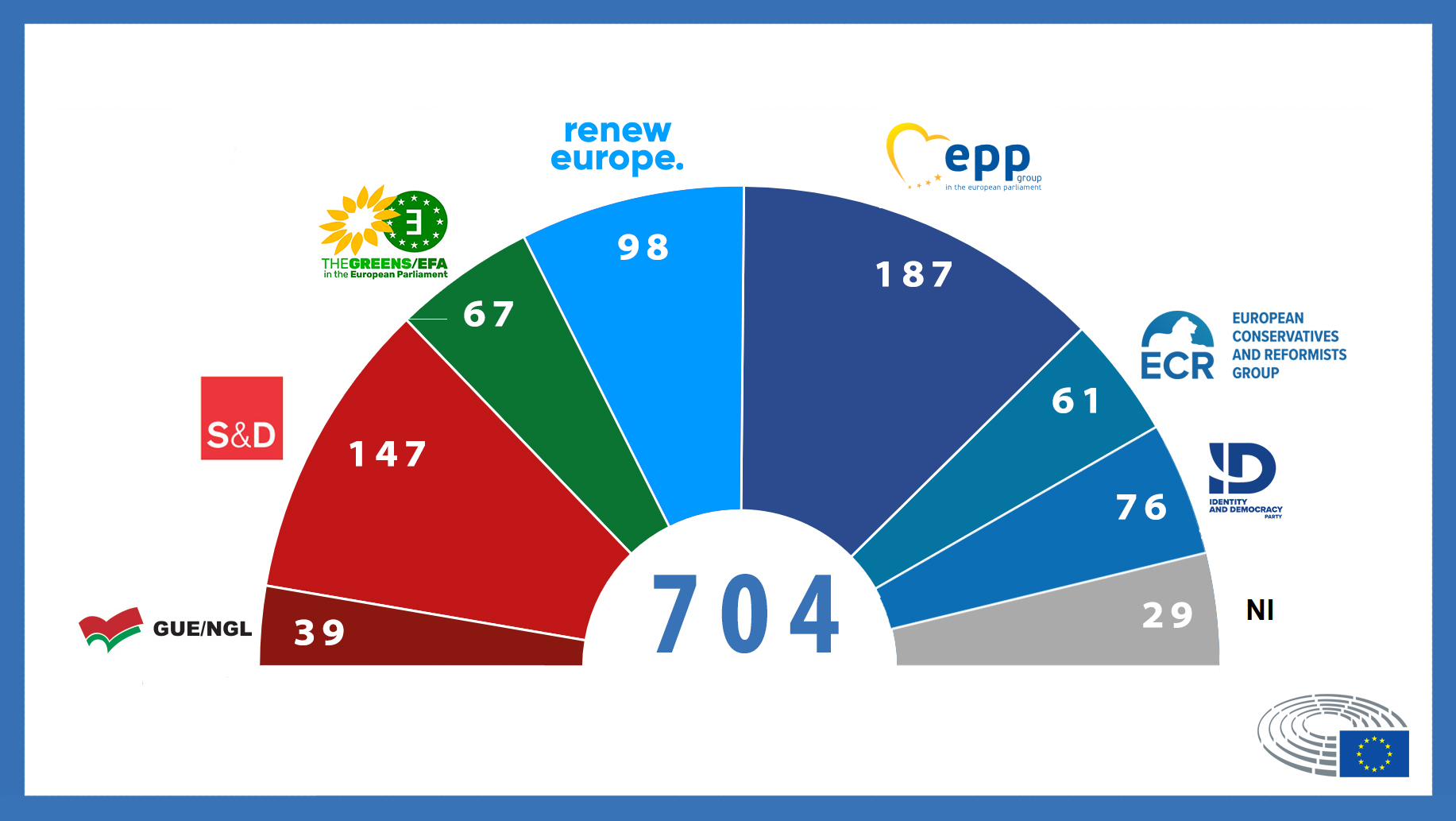 Abbildung 2: Die Sitzordnung im Europäschen Parlament. NI sind Parteilose
Abbildung 2: Die Sitzordnung im Europäschen Parlament. NI sind Parteilose
Evaluation des Ergebnisses
Das Verhältnis von GUE/NGL, S&D, GREENS/EFA zeigt sehr deutlich den Nutzen der Erkennung von überlappenden Gemeinschaften. Wie zu sehen ist, ist die Farbgebung von GREENS/EFA eine Mischung der anderen beiden. Wie auch an den Kanten zu sehen sind sich Mitglieder dieser Fraktion und der beiden anderen häufig einig oder uneinig. Da sie jedoch den gleichen Gemeinschaften zugeordnet werden, kann man davon ausgehen, dass sie sich einig sind. Diese klare Einigkeit besteht jedoch nicht zwischen S&D und GUE/NGL. Als Folge würde das Borgia Clustering an dieser Stelle alle Abgeordneten der drei Parteien einer Gemeinschaft zuordnen, oder sie in unterschiedliche Gemeinschaften aufteilen, was dazu führen würde, dass nicht mehr deutlich ist wie ähnlich diese Fraktionen abstimmen. Beziehungsweise würde die Kantenanzahl darauf hindeuten, jedoch würde diese allein keine Aussage über positive oder negative Beziehungen treffen.

Abbildung 3: Linke, Sozial-Demokraten und Grüne im Detail
Eine weitere Auffälligkeit die sich beobachten lässt, ist die Uneinigkeit innerhalb der rechtspopulistischen / EU-skeptischen Fraktionen. Während die Linken, Sozialisten, Grüne innerhalb ihrer Fraktion fast identisch den Gemeinschaften zugeordnet werden, zeichnet sich auf der anderen Seite des politischen Spektrums ein anderes Bild ab.

Abbildung 4: ID (Identität und Demokratie) und ECR (Europäische Konservative und Reformer) im Detail
Das gesamte Ergebnis wird von den Arbeiten zum Europaparlament von 1999 - 2004 (HIX & NOURY, 2009) und zum 6. Europaparlament (2014-2019) (Cherepnalkoski et al., 2016) unterstützt. Diese ergaben, dass sowohl Fraktionen am rechten Rand als auch die Fraktionslosen eine geringere Kohäsion bei Abstimmungen besitzen als alle Fraktionen im Durchschnitt.

Abbildung 5: Übereinstimmung bei Abstimmungen innerhalb der Parteien im Europäischen Parlament 2014-2019
Außerdem bestätigen Hix und Noury in ihrer Arbeit(HIX & NOURY, 2009) unser Beispiel der Kohäsion zwischen Grünen, Linken und Sozialdemokraten.
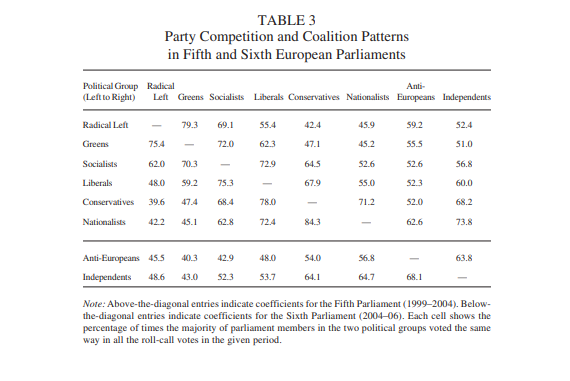
Es besteht sowohl zwischen Linken und Grünen und zwischen Grünen und Sozialdemokraten eine hohe Einigkeit mit einer Übereinstimmung von jeweils >70% (6. Europaparlament). Linke und Sozialdemokraten haben im gleichen Zeitraum eine min. 12% geringere Übereinstimmung mit 62%. Im 5. Europaparlament waren alle Werte höher, besonders die Kohäsion von Linken und Sozialdemokraten. Dies könnte einen weiteren zukünftigen Rückgang der Kohäsion zwischen diesen Fraktionen andeuten und die direkte Unabhängigkeit der beiden Parteien in unserem Ergebnis erklären. Dieser Rückgang wird tatsächlich in (Cherepnalkoski et al., 2016) bestätigt.
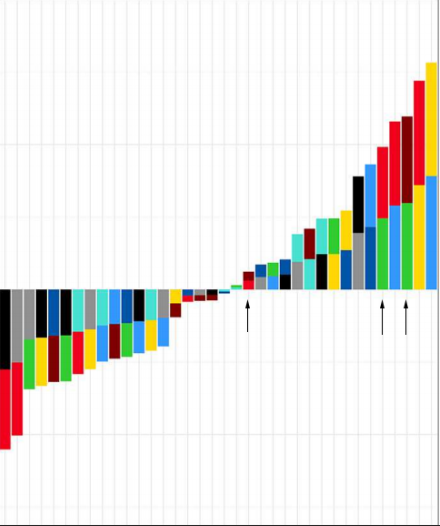
Abbildung 6: Für jedes Fraktionskombinationspaar gibt es eine Säule. Positive Werte entsprechen Einigkeit zwischen den entsprechenden Fraktionen, negative Werte Uneinigkeit
Fazit
Da die Richtigkeit des Ergebnisses des Signed DMID Algorithmus wissenschaftlich belegt werden kann, lässt sich sagen, dass die Analyse dieses Netzwerks korrekt war. Aus der hohen Bedeutung von überlappenden Gemeinschaften und negativen Kantengewichten lässt sich somit schließen, dass das Borgia Clustering, ohne essenzielle Erweiterungen nicht dazu geeignet ist, vorzeichenbehaftete Netzwerke zu analysieren. Außerdem ist es nur zur Analyse von einfacher Community Detection geeignet.
Zusammenfassung
Nach genauerer Betrachtung des Borgia Clustering werden Schwächen des Algorithmus ersichtlich, die dessen Anwendungsfeld einschränken. Die Anwendung des Signed DMID Algorithmus auf einem Netzwerk, dass das Europäische Parlament modellierte, zeigte, dass das Borgia Clustering weder geeignet für vorzeichenbehafteten Netzwerken ist, noch zur Overlapping Community Detection angewendet werden kann. Die Methodik des Borgia Clustering ermöglicht jedoch interessante Analysen von Netzwerken. Mit geeigneten Erweiterungen des Algorithmus könnte einen wertvollen Beitrag zu OCDA auf vorzeichenbehafteten Netzwerken leisten.
Referenzen
- Xie, J., Kelley, S., & Szymanski, B. K. (2013). Overlapping community detection in networks. ACM Computing Surveys, 45(4), 1–35. https://doi.org/10.1145/2501654.2501657
- Kim, H., & Kang, H. (2020). Graph Neural Network in Biologie (3rd ed.). http://ocd.git.dbis.rwth-aachen.de/Online-Buch/Auflage_3/GNN//index.html
- Shahriari, M., & Klamma, R. (8252015). Signed Social Networks. In J. Pei, F. Silvestri, & J. Tang (Eds.), Proceedings of the 2015 IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining 2015 (pp. 1608–1609). ACM. https://doi.org/10.1145/2808797.2809357
- Wright, W. E. (1977). Gravitational clustering. Pattern Recognition, 9(3), 151–166. https://doi.org/10.1016/0031-3203(77)90013-9
- Fumanal-Idocin, J., Alonso-Betanzos, A., Cordón, O., Bustince, H., & Minárová, M. (2020). Community detection and social network analysis based on the Italian wars of the 15th century. Future Generation Computer Systems, 113, 25–40. https://doi.org/10.1016/j.future.2020.06.030
- Schliewe, D., & Gries, F. (2020). Politische und Ökonomische Netzwerke (3rd ed.). http://ocd.git.dbis.rwth-aachen.de/Online-Buch/Auflage_3/PON/index.html
- Robin De Baets. (2020). Gravitational Clustering Visualization. https://www.youtube.com/watch?v=0SHRdmkzgJM
- Gupta, M. M., & Qi, J. (1991). Theory of T-norms and fuzzy inference methods. Fuzzy Sets and Systems, 40(3), 431–450. https://doi.org/10.1016/0165-0114(91)90171-L
- Reid, F., McDaid, A., & Hurley, N. (2013). Partitioning Breaks Communities. In T. Özyer, Z. Erdem, J. Rokne, & S. Khoury (Eds.), Mining Social Networks and Security Informatics (pp. 79–105). Springer Netherlands. https://doi.org/10.1007/978-94-007-6359-3\textunderscore 5
- European Parliament. (2021). Results of votes. https://www.europarl.europa.eu/plenary/en/votes.html?tab=votes
- HIX, S. I. M. O. N., & NOURY, A. B. D. U. L. (2009). After Enlargement: Voting Patterns in the Sixth European Parliament. Legislative Studies Quarterly, 34(2), 159–174. https://doi.org/10.3162/036298009788314282
- Cherepnalkoski, D., Karpf, A., Mozetič, I., & Grčar, M. (2016). Cohesion and Coalition Formation in the European Parliament: Roll-Call Votes and Twitter Activities. PloS One, 11(11), e0166586. https://doi.org/10.1371/journal.pone.0166586