Abstract

Soziale Medien gewannen in den letzten Jahren immer mehr an Bedeutung, damit auch ihre Communities sowie das Erkennen bzw. Betrachten dieser. Aber auch andere Felder, die große Mengen an verknüpften Datenpunken verwenden, wie zum Beispiel die Biologie und Physik profitieren davon untere Netzwerke schnell und verlässlich zu finden. Die hier vorgestellte Methode Modularity Optimization, ist das Maximieren der Modularität im Netzwerk, was bedeutet, die Gruppen so zu wählen, dass die Punkte möglichst eng vernetzt sind. Der Algorithmus verwendet Modularity Optimization, indem er die Punkte in andere Gruppen verschiebt und prüft, ob eine Verbesserung der Modularität stattgefunden hat. Dabei werden viele Umstände berücksichtigt, die die Laufzeit verbessern, um selbst bei größeren Netzwerken noch schnell Lösungen zu finden. Bei der Modularity Optimization ist eine hohe Auflösung eine häufig vernachlässigte Eigenschaft, da diese die Laufzeit deutlich erhöht. Wir berücksichtigen dies und können unseren Algorithmus leicht modifizieren, um deutlich höhere Auflösungen zu erziehlen, gegen genannte Nachteile.

1) Einleitung

In den vergangenen Jahren und Jahrzehnten wurden komplexe Systeme ein immer wichtiger werdendes Thema in nahezu allen Bereichen der Wissenschaft. Zur Darstellung dieser wurden, egal ob Biologie(Gavin et al., 2006)(Krogan et al., 2006), Informatik(Smith & Kollock, 1999) oder Soziologie(Pizzuti, 2008), Netzwerke benutzt, welche mathematisch als Graph dargestellt werden können. Dabei werden Verbindungen und Interaktionen zwischen den Komponenten eines Systems als Kanten (edges) und die Komponenten als Knoten (nodes) vertreten. Praktische Anwendungen sind beispielsweise Hyperlinks auf Webseiten(Smith & Kollock, 1999), Verbindungen zwischen Neuronen im Gehirn(Ahn et al., 2010) oder auch Interaktionen zwischen Teilnehmern eines sozialen Netzwerks [1,6]. Sie alle können als ungerichteter Graph dargestellt und modelliert werden. Basierend auf der naheliegenden Hypothese, dass die Interaktionen der Komponenten das charakteristische Merkmal eines Netzwerks sind, wurden immer wieder Algorithmen entwickelt, um Communities in solchen Netzwerken zu finden. Eine bekannte Methode, um Communities in solchen Netzwerken zu finden ist es, die Modularität in einem Netzwerk(Newman, Mark E. J. & Girvan, 2004) zu berechnen und aufgrund dessen den Graph zu analysieren und herauszufinden, welche Menge von Knoten in dem Netzwerk eine Community darstellen könnte. Dabei ist es wichtig zuallererst zu definieren, was eine Community ist. Da es zum jetzigen Stand der Wissenschaft keine allgemeingültige Definition(Maoguo Gong et al., 2012) gibt benutzen wir hier die Definition von Girvan und Newman(Girvan & Newman, 2002), welche eine Community als Gruppe von Knoten, welche eine höhere Interaktion innerhalb der Gruppe vorweisen und eine niedrigere Interaktion außerhalb der Gruppe (Abbildung 1). Mit dieser Definition können wir nun auch das Problem definieren: Einen Algorithmus, der ein Netzwerk so optimiert, dass alle Communities gefunden und voneinander getrennt dargestellt werden können. Von solchen Algorithmen, die Netzwerke optimieren um Communities zu entdecken, gibt es bereits viele gute und effiziente Algorithmen(Fortunato, 2010). Die Algorithmen, die dabei auf der Modularität, definiert nach Girvan und Newman(Newman, Mark E. J. & Girvan, 2004), basieren spielen in der Familie der Optimierungsalgorithmen bereits eine große Rolle. Die Modularität wird dabei als ein Qualitätsmerkmal gesehen, welches die Konzentration von Kanten in einer Community mit der Konzentration von Kanten in einem zufälligen Graphen vergleicht. Ein höherer Wert der Modularität ist demnach ein Zeichen dafür, dass sich eine Community stärker von einem zufälligen Graphen abhebt und sich somit eine bessere Struktur von Communities innerhalb des Netzwerks finden lässt. Um dieses Ziel zu erreichen muss das Problem als kombinatorisches Problem definiert werden, mit dem Ziel, die Modularität zu maximieren. In einem Graph \(G = (V, E)\) mit der Adjazenzmatix A kann die Modularität folgendermaßen mathematisch dargestellt werden: \(Q = ∑_{(c=1)} [lc/m - (dc/2m)]\)
wobei m die Summe aller Kanten im Graph, k die Communities des Netzwerks, \(lc\) die Anzahl an Kanten in der Community \(c\) und dc die Summe der Grade aller Knoten in der Community c darstellt. Auch wenn die Optimierung von Netzwerken durch Modularität eine derjenigen Methoden ist, die am weitesten verbreitet ist und am besten funktioniert, gibt es einige Einschränkungen hinsichtlich des Findens von Communities(Good et al., 2010). So passiert es oft, dass Gruppen als Communities gezählt werden, auch wenn sie hinsichtlich der Größe in Relation zum Netzwerk zu klein sind, um eine Community darzustellen. Mit dem hier vorgestellten Algorithmus versuchen wir, dieses Problem anzugehen und trotzdem noch Ergebnisse erzielen, die hinsichtlich der Effizienz und der Menge an benötigten Ressourcen mit anderen aktuellen Community-Algorithmen konkurrieren können.

2) Algorithmus / Algorithmen als Pseudo-Code

Der hier vorgestellte Algorithmus verwendet die Modularität nach Girvan und Newman (Newman, Mark E. J. & Girvan, 2004) und benötigt eine Adjazenzmatrix mit allen Knoten des sozialen Netzwerks, welche für \(A_ij\) 1 ist, wenn eine Kante zwischen den beiden Knoten besteht und ansonsten 0 ist. Er basiert auf dem MA-Net Algorithmus von Naeni, Berretta und Moscato(Moslemi Naeni et al., 2014).

Eingabe: Adjazenzmatrix \(A_ij\) Maximale Anzahl an Versuchen ohne eine Verbesserung: \(x\)

Resultat Adjazenzmatrix \(A_ij\) with added communitylabels.

laenge          <-      |Knoten| im sozialen Netzwerk.
anzahlKanten    <-      |kanten| im sozialen Netzwerk.
tbd             <-      Anzahl der zu generierenden Lösungen. Eine höhere Anzahl bedeuted mehr Vielfalt.
loesungen       <- 	    Initialisiere die loesungen indem Knoten zufällige Community labels bekommen.
loesungen.migriere() 	Jeder Knoten schaut ob er in einer Nachbar-Community besser aufgehoben wäre.

while (ausfallkriterium_nicht_erfüllt) do {
    loesungen.kreuze()      <-  Nehme jeweils zwei Lösungen und behalte deren besten Communities und löse die Schlechtesten auf.
    loesungen.mutiere()	    <-  Jeder Knoten kann ohne Verbesserung zu einer Nachbar Community wechseln.
									Die Wahrscheinlichkeit steigt mit jedem Durchlauf ohne Verbesserung.
    if(loesungen habens sich für x versuche nicht verbessert)
	    ausfallkriterium_nicht_erfüllt <- false
}

2.1) Initialisierung und Darstellung:

Das Netzwerk wird als Adjazenz Matrix aller Knoten im Netzwerk dargestellt, in der \(A_ij\) 1 ist, falls eine Kante zwischen den Knoten besteht und ansonsten 0 ist. Außerdem initialisieren wir die Variablen length mit der Anzahl aller Knoten im Netzwerk, numberOfEdges mit der Anzahl aller Kanten im Netzwerk, tbd mit der Anzahl der gewünschten Initiallösungen und solutions initialisieren wir mit einer Menge von Netzwerken, die zufällig gewählte Communities beinhalten. Dementsprechend benötigt der vorgestellte Algorithmus keine Annahmen darüber, wieviele Communities es gibt, könnte diese allerdings auch nicht verwerten. Außerdem muss gesagt werden, dass die zufällig gewählten Communities keine qualitativ hochwertigen Communities darstellen, sondern lediglich als erste Startannahmen dienen, damit auf diesem Netzwerk, mit bereits bestehenden Communities, verschiedene Methoden laufen können, um die Communities zu verbessern und zu optimieren.

2.2) Migration:

Die Migrationsmethode (solutions.migrate) schaut für jeden Knoten, ob sich die Modularität im Netzwerk erhöht, wenn dieser in die Community des Nachbarknoten migriert. Sollte dies der Fall sein, so geschieht das auch, wenn nicht, dann bleiben die Knoten in deren herkömmlichen Communities.

2.3) Mutation:

Knoten können auch zum Nachbarn migrieren, ohne eine Verbesserung der Modularität zu bekommen. Dazu gibt es eine gewisse adaptive Wahrscheinlichkeit, dass Knoten \(a\) in eine Community seines Nachbarknotens \(b\) migriert. Diese adaptive Wahrscheinlichkeit erhöht sich mit jedem Mal, bei dem eine Migration keine Erhöhung der Modularität erzeugt.

2.4) Kombination der Communities:

Um aus der Menge an Netzwerken eine Verbesserung herzustellen muss man diese miteinander kombinieren. Da man durch die vorherige Migrationsmethode davon ausgehen kann, dass sich nun Communities mit relativ hoher Qualität in den Netzwerken befinden werden diese miteinander kombiniert. Dazu nimmt man zwei zufällige Netzwerke und vereint diese. Das Netzwerk, welches herauskommt, beinhaltet dann die jeweils besten Communities der beiden ursprünglichen Netzwerke.

3) Ergebnisse

Hier stellen wir unsere Ergebnisse vor, die der Algorithmus auf verschiedenen Netzwerken erzielt hat. Implementiert wurde der Algorithmus in Java 8 und getestet auf einem AMD Ryzen 7 1800X mit 4.0GHz und 8 Kernen. Der RAM war 16GB groß. Um ein genaueres Ergebnis zu erzielen haben wir den Algorithmus mehrmals auf den einzelnen Netzwerken getestet. Dabei haben wir die Netzwerke Les Misérables (Universität Koblenz) und Facebook (NIPS) (Universität Koblenz) benutzt.

3.1) Les Misérables:

Dieses Netzwerk von der Universität in Koblenz besitzt eine Größe von 77 Knoten. Die Knoten werden durch 254 ungerichtete Kanten verbunden. Dieses Netzwerk stellt die Charaktere aus der Novelle von Victor Hugo „Les Misérables“ dar. Die einzelnen Charaktere werden dabei als Knoten dargestellt und es besteht eine Verbindung zwischen diesen, wenn die beiden Charaktere gleichzeitig im Buch vorkommen.

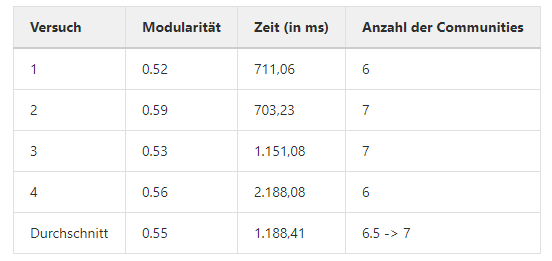
3.2) Facebook (NIPS):

Dieses Netzwerk der Universität Koblenz besitzt eine Größe von 2.888 Knoten, die durch 2.981 ungerichtete Kanten verbunden werden. Das Netzwerk stellt ein soziales Netzwerk (Facebook) dar. Ein Knoten stellt einen Nutzer dar und eine Kante stellt eine Freundschaft zwischen diesen Nutzern dar.

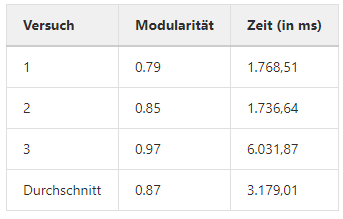
3.3) Vergleichen:

Wir vergleichen nun also die Ergebnisse dieses Algorithmus‘ mit anderen Algorithmen, die auf Modularität basieren. Dabei beziehen wir uns auf das Netzwerk Facebook (NIPS), auf welchem wir die Ergebnisse bereits oben dargestellt haben. Da die Algorithmen auf unterschiedlichen Rechnern gelaufen sind, können wir die Zeitkomponente leider nicht mit einbeziehen.

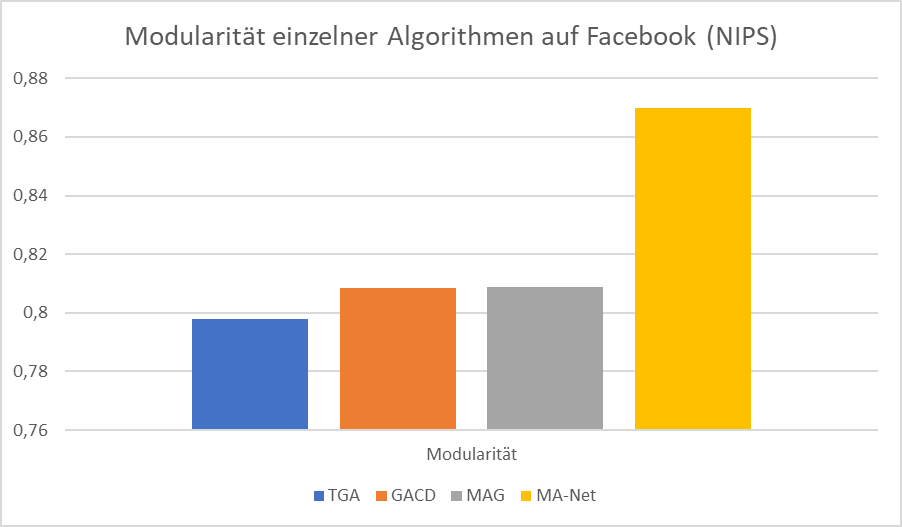
Wir beziehen uns hierbei auf die Algorithmen aus dem Buch From Security to Community Detection in Social Networking Platforms(Karampelas et al., 2019). Dabei kann man erkenne, dass der vorgestellte Algorithmus MA-Net eine deutlich höhere Modularität auf demselben Netzwerk erzeugt, als andere aktuelle Algorithmen.

4) Ausblick

Man kann davon ausgehen, dass Netzwerke und Algorithmen, um Communities in solchen zu identifizieren auch in Zukunft ein immer wichtiger werdendes Themenfeld werden wird. Die Probleme, die dabei auftreten, werden unzählig sein und sind jetzt noch nicht absehbar. Mit unserem Algorithmus haben wir nicht nur einen Algorithmus entwickelt, der bessere Ergebnisse als herkömmliche Algorithmen liefert, sondern zudem noch sehr simpel und effizient ist. Mit einigen wenigen Methoden ist es gelungen, eine gute Basis für zukünftige Algorithmen herzustellen und zudem noch eines der größten Probleme, das Finden und Bilden von kleinen Communities, zu verringern. Dieses Problem gilt es auch in Zukunft weiterhin zu lösen. Außerdem muss daran gearbeitet werden, die Effizienz dieses Algorithmus‘ auf großen Netzwerken noch zu erhöhen, damit die immer größer werdenden Netzwerke auch in Zukunft in einer passablen Zeit in einzelne Communities unterteilt werden können.

5) Referenzen

Gavin, A.-C., Aloy, P., Grandi, P., Krause, R., Boesche, M., Marzioch, M., Rau, C., Jensen, L. J., Bastuck, S., Dümpelfeld, B., Edelmann, A., Heurtier, M.-A., Hoffman, V., Hoefert, C., Klein, K., Hudak, M., Michon, A.-M., Schelder, M., Schirle, M., … Superti-Furga, G. (2006). Proteome survey reveals modularity of the yeast cell machinery. Nature, 440(7084), 631–636. https://doi.org/10.1038/nature04532
Krogan, N. J., Cagney, G., Yu, H., Zhong, G., Guo, X., Ignatchenko, A., Li, J., Pu, S., Datta, N., Tikuisis, A. P., Punna, T., Peregrín-Alvarez, J. M., Shales, M., Zhang, X., Davey, M., Robinson, M. D., Paccanaro, A., Bray, J. E., Sheung, A., … Greenblatt, J. F. (2006). Global landscape of protein complexes in the yeast Saccharomyces cerevisiae. Nature, 440(7084), 637–643. https://doi.org/10.1038/nature04670
Smith, M. A., & Kollock, P. (Eds.). (1999). Communities in Cyberspace. Routledge.
Pizzuti, C. (2008). GA-Net: A Genetic Algorithm for Community Detection in Social Networks. In G. Rudolph, T. Jansen, N. Beume, S. Lucas, & C. Poloni (Eds.), Parallel Problem Solving from Nature – PPSN X (pp. 1081–1090). Springer Berlin Heidelberg.
Ahn, Y.-Y., Bagrow, J. P., & Lehmann, S. (2010). Link communities reveal multiscale complexity in networks. Nature, 466(7307), 761–764. https://doi.org/10.1038/nature09182
Newman, Mark E. J., & Girvan, M. (2004). Finding and Evaluating Community Structure in Networks. Physical Review, 69(026113).
Maoguo Gong, Qing Cai, Yangyang Li, & Jingjing Ma. (2012). An improved memetic algorithm for community detection in complex networks. 2012 IEEE Congress on Evolutionary Computation, 1–8. https://doi.org/10.1109/CEC.2012.6252971
Girvan, M., & Newman, M. E. J. (2002). Community structure in social and biological networks. Proceedings of the National Academy of Sciences, 99(12), 7821–7826. https://doi.org/10.1073/pnas.122653799
Fortunato, S. (2010). Community detection in graphs. Physics Reports, 486(3-5), 75–174. https://doi.org/10.1016/j.physrep.2009.11.002
Good, B. H., de Montjoye, Y.-A., & Clauset, A. (2010). Performance of modularity maximization in practical contexts. Physical Review. E, Statistical, Nonlinear, and Soft Matter Physics, 81(4 Pt 2), 046106. https://doi.org/10.1103/PhysRevE.81.046106
Moslemi Naeni, L., Berretta, R., & Moscato, P. (2014). MA-Net: A reliable memetic algorithm for community detection by modularity optimization (Springer-Verlag Berlin Heidelberg, Ed.). https://www.researchgate.net/profile/Leila_Naeni/publication/269519801_MA-Net_A_Reliable_Memetic_Algorithm_for_Community_Detection_by_Modularity_Optimization/links/5577e5fa08aeacff200051ef/MA-Net-A-Reliable-Memetic-Algorithm-for-Community-Detection-by-Modularity-Optimization.pdf
Karampelas, P., Kawash, J., & Özyer, T. (Eds.). (2019). From Security to Community Detection in Social Networking Platforms. Springer International Publishing. https://doi.org/10.1007/978-3-030-11286-8