Random Walks auf vorzeichenbehafteten Netzwerken
| Malte Knuth | Mohammad Mahdi Khalily | ||
|---|---|---|---|
| RWTH Aachen University | RWTH Aachen University | ||
| malte.knuth@rwth-aachen.de | mahdi.khalily@rwth-aachen.de |
Abstract
Vor allem in der Politik und Wirtschaft spielen soziale Netzwerke eine immer größere Rolle im Bezug auf Ideenaustausch und Meinungsmache. Durch das hohe Interesse und durch die Aussagekraft sozialer Netzwerke über die Gesellschaft nimmt die Relevanz von Algorithmen zur Analyse solcher Netzwerke weiter zu. Außerdem besteht das Interesse daran Inhalte bzw. Werbeanzeigen gezielt gewünschten Communities nahe zu bringen. Auf Grund der Größe von echten vorzeichenbehafteten Netzwerken ist die Erkennung von Communities in diesen Netzwerken sehr rechenaufwendig. In diesem Kapitel gehen wir darauf ein wie ein solcher Algorithmus bei dem Prozess zu Findung von Communities effizienter entwickelt werden kann. Anschließend werden wir mit Hilfe von konkreten Beispielen den Unterschied zwischen der Erweiterung und den Vorgängermodellen veranschaulichen sowie die Vorteile des Sigend Random Walk with Restart im Vergleich mit ähnlichen Algorithmen hervorheben.
Inhaltsverzeichnis
1.Einleitung
Durch die Einführung von positiven und negativen Beziehungen in sozialen Netzwerken, ist ein weiterer interessanter Punkt zur Findung von Communities in Netzwerken zu beachten. Mit Hilfe der gewerteten Beziehungen ist es möglich eine bessere Darstellung und Bewertung zwischen Personen zu entwickeln. Eine solche Bewertung kann als eine geeignete Rangstruktur dargestellt werden, die Beziehungen einer Person mit allen Personen im sozialen Umfeld einstuft. Mit dieser Rangstruktur kann man wissen welchen Einfluss eine bestimmte Person auf andere hat und das ist besonders für Bereiche im Marketing und der Politik sehr wertvoll, aber auch in der Suche nach Communities können diese Informationen hilfreich sein.
Betrachtet man die Personen und ihre Beziehungen als einen gewichteten Graphen, so gibt es einige Algorithmen, die ein solches Ranking berechen. Die bekanntesten Algorithmen die auf einem random-walk basieren sind der PageRank und der Random Walk with Restart. Diese wurden bereits in Auflage 2 dieses Buches betrachtet, sie liefern allerdings kein hinreichendes Ergebnis auf Netzwerken mit gewichteten Beziehungen und betrachten nur positive Verbindungen. Im Folgenden betrachten wir den Signed Random Walk with Restart(SRWR), ein neuer Random Walk basierender Algorithmus, der die gewichteten Beziehungen einbezieht und eine und damit eine sinnvolle Rangstruktur entwickelt. Dabei betrachten wir zwei Varianten dieses Algorithmuses mit dem SRWR-ITER einer iterativen Version und dem SRWR-PRE eine Version zur schnellen Findung eines geeigneten Ergebnisses.(Jung et al., 2020)
Übersicht über unsere Variabeln in den folgenden Abschnitten
2.Verwandte Arbeiten
Random Walk Algorithmen auf ungewichteten Graphen.
Da die meisten Algorithmen für gewichtete Graphen Erweiterungen von Algorithmen sind, die auf ungewichteten Graphen arbeiten, kann man in diesem Bereich viele originale Algorithmen finden. Zum Beispiel SALSA(The Sochastic approach for link-structure analysis) oder auch Page Rank und Random Walk, die auch in diesem Buch in der Auflage 2 betrachtet wurden. Diese Algorithmen sind allerdings für ungwichtete Graphen entwickelt und damit nicht für gewichtete Graphen geeignet(Backstrom & Leskovec, 2011).
Signed-PageRank
Neben dem Signed Random Walk wiht Restart gibt es auch andere Algorithmen deren Ziel ist eine Rankstruktur zu erstellen. Eine ähnliche Randowm Walk Variante ist der Signed-PageRank mit dem Ziel zu erkennen welche Personen den maximalen Einfluss vor allem im Bereich Marketing hat. Dabei wird die Art der Informationsverbreitung in sozialen Medien mit der Ausbreitung von Krankheiten verglichen und Modelle für die Krankheitsausbreitungen modifiziert und auf soziale Netzwerke für Marketingzwecke angepasst(Yin et al., 2019).
3.Methodik
In diesem Abschnitt betrachten wir den Algorithmus Signed Random Walk with Restart(SRWR) entwickelt bei (Jung et al., 2020). Dabei gehen wir zuerst auf die generelle Idee ein und werfen dann einen Blick auf die zwei Varianten den SRWR-ITER und den SRWR-PRE.
Signed Random Walk with Restart
Für diesen Algorithmus betrachten wir soziale Netzwerke als gewichtet Graphen, mit dem Ziel eine Rangstruktur zu entwickeln zur Bewertung wie sehr der Startknoten allen anderen Knoten vertraut.
Die Eingabe für den Algorithmus ist ein gewichteter Graph sowie ein Startknoten s für den eine Rangstruktur entwickelt wird.
Als Idee wird ein sogenannter Random-Surfer(Jung et al., 2020) eingeführt, dieser Surfer startet an dem Knoten s und wählt einen zufälligen
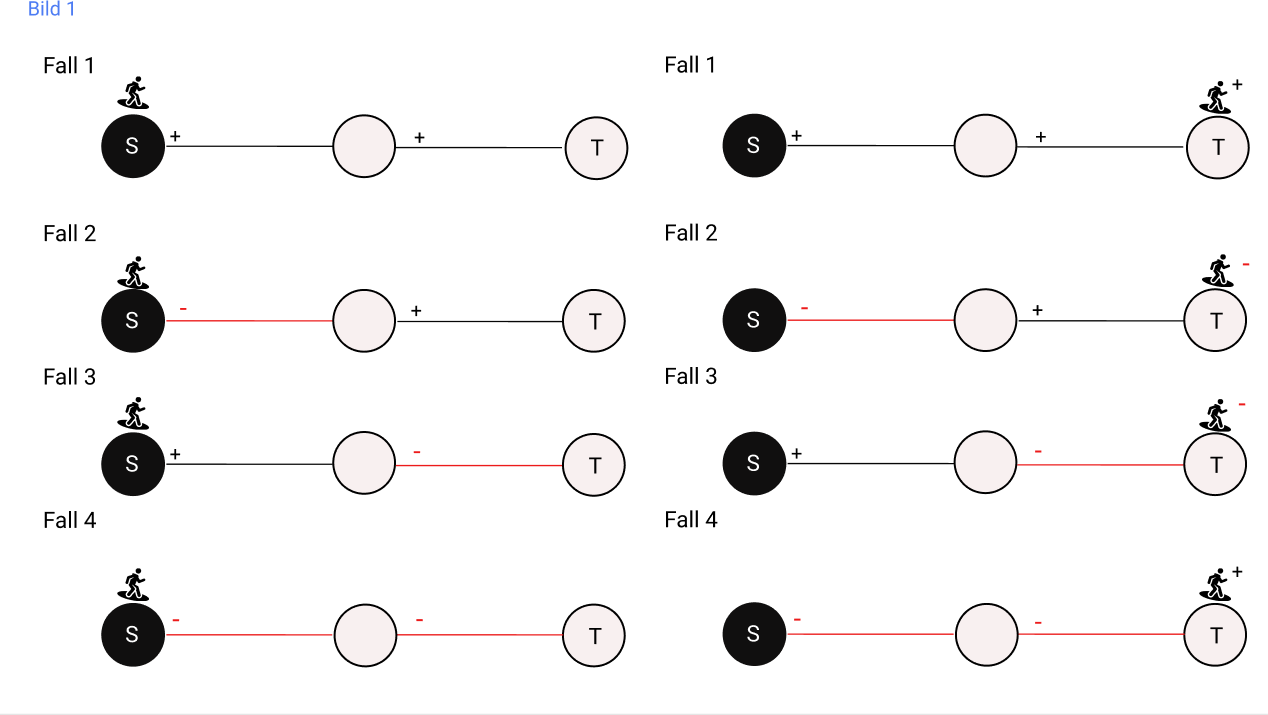
Weg zu einem Nachbarn von s. Hierbei sind 4 Fälle zu betrachten je nach freundlicher oder feindlicher Einstellung zum Nachbarn wie in Bild 1 aufgeführt.
Fall 1: Freund eines Freundes; Fall 2: Freund eines Feindes; Fall 3:Feind eines Freundes; Fall 4: Feind eines Feindes.
In allen Fällen ist die Strategie eine Änderung der Einstellung des Surfers immer wenn er einen negativen Pfad passiert, der Surfer startet mit einer positiven
Einstellung und ändert diese sobald die erste negative Beziehung betrachtet wird.
So wird als Beispiel im Fall 4 der Feind eines Feindes als Freund betrachtet, aber in Fall 2 der Freund eines Feindes als Feind.
Um zu berechnen inwiefern der Knoten s einem Knoten t vertraut wird ausgewertet wie oft der Knoten t vom Surfer
mit einer positiven Einstellung im Vergleich zu einer negativen Eistellung besucht wurde.
Der SRWR besteht aus zwei Aktionen dem zufälligen Bewegen des Surfers zu einem Nachbarn und dem Restart,
der Restart wird mit einer Wahrscheinlichkeit c festgelegt und bringt den Surfer mit positiver Einstellung zurück zum Startknoten(Jung et al., 2020).
Die zwei wichtigsten Messwerte, die zu betrachten sind, sind die Wahrscheinlichkeiten für einen Knoten vom Surfer mit positiver \(r^+\) oder negativer \(r^-\) Einstellung besucht zu werden.
Dabei können beide Werte einzelnd betrachtet werden oder ein Vertrauenswert \(r = r^+ - r^-\) für jeden Knoten berechnet werden. Der Wert r kann also drei Fälle beschreiben:
Wird der Knoten t nur oder hauptsächlich mit positiver Einstellung des Surfers besucht, so vertraut s dem Knoten t.
Ist die Einstellung des Surfers bei Besuchen von t in der Anzahl von negativen und positiven ausgeglichen(einem Wert zwischen -1 und 1(Jung et al., 2020)) wird eine neutrale Haltung von s zu t eingenommen. Und zuletzt wenn der Knoten t überwiegend mit einer negativen Einstellung besucht wird, so schenkt s dem Knoten t kein Vertrauen.
Mathematische Formulierung für SRWR
Wir beschreiben die Werte für \(r^+\) und \(r^-\) dabei betrachten wir ein Beispiel in Bild 2.
Sei \(r^{+}_u(t+1)\) die Wahrscheinlichkeit, dass der Surfer von dem Knoten s gestartet ist und zum Zeitpunkt t+1 mit positiver Einstellung bei u ankommt und \(r^{-}_u(t+1)\) analog für eine negative Einstellung.
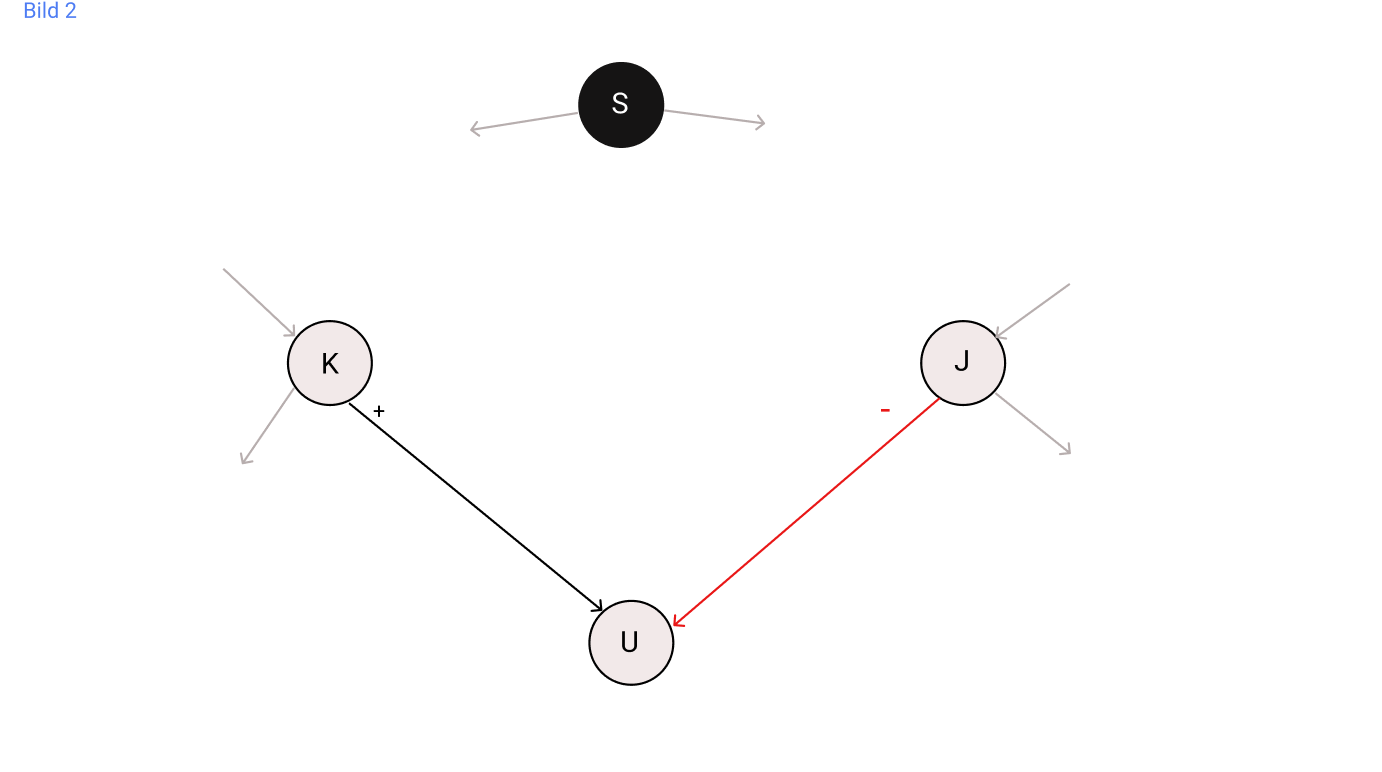
Nun muss zum Zeitpunkt t der Surfer bei einem Nachbarn von u sein und für jeden Nachbarn mit einer positiven Beziehung zu u nehmen wir die Wahrscheinlichkeit, dass der Surfer mit positiver Einstellung dort am Zeitpunkt t ist (für Nachbarn mit negativer Beziehung wird der Surfer mit negativer Einstellung betrachtet). Jetzt muss noch die Wahrscheinlichkeit, ob der Surfer vom Nachbarn auch zu u übergeht, einbezogen werden. Im Beispiel hat j zwei ausgehende Pfade und eine negative Einstellung zu u d.h. wir schauen, wie wahrscheinlich ist zum Zeitpunkt t der negative Surfer bei dem Nachbarn j beschrieben durch \(r^{-}_j\) und mit welcher Wahrscheinlichkeit begibt sich der Surfer im nächsten Schritt t+1 zu u, da wir 2 Pfade von j haben ist dies
0,5. Damit erhalten wir für den Nachbarn j den Wert \(\frac{r^{-}_j}{2}\) dieser Wert muss mit dem Wert aller anderen Nachbarn summiert werden und dadurch erhalten wir folgende Formeln.
\(r^{+}_{u}(t+1) = (1-c) \Big(\frac{r^{-}_j(t)}{2} + \frac{r^{+}_k(t)}{2}\Big) + c1(u =s)\)
\(r^{-}_{u}(t+1) = (1-c) \Big(\frac{r^{+}_j(t)}{2} + \frac{r^{-}_k(t)}{2}\Big)\)
Wobei (1-c) die Möglichkeit eines Restarts und c1(u=s) den Fall, dass der Startknoten betrachtet wird ist.
Allgemein erhalten wir dann:
\(r^{+}_{u}(t+1) = (1-c) \Big(\sum\limits_{v\in \overleftarrow{N^{+}_v}}\frac{r^{-}_v(t)}{\vert\overrightarrow{N_v}\vert} +\sum\limits_{v\in \overleftarrow{N^{-}_v}} \frac{r^{-}_v(t)}{\vert \overrightarrow{N_v}\vert}\Big) + c1(u =s)\)
\(r^{-}_{u}(t+1) = (1-c) \Big(\sum\limits_{v\in \overleftarrow{N^{-}_v}}\frac{r^{+}_v(t)}{\vert\overrightarrow{N_v}\vert} + \sum\limits_{v\in \overleftarrow{N^{+}_v}} \frac{r^{-}_v(t)}{\vert \overrightarrow{N_v}\vert}\Big)\)
(Jung et al., 2020)
Mit \(\overleftarrow{N_v}\) als der Menge der eingehenden Nachbarn von v und \(\overrightarrow{N_v}\) die Menge der ausgehenden Nachbarn von v.
SRWR-ITER
Die Variante des Signed Random Walk with Restart SRWR-ITER nutzt eine iterative Strategie, um diese recursiven Formeln zu lösen. Dabei geht SRWR-ITER in zwei Phasen vor:
Die erste Phase ist die Normalisierungsphase:
Zuerst wird eine Matrix D berechnet, die die Anzahl an Nachbarn für jeden Knoten in A bestimmt. Mithilfe der Matrix D wird eine teilweise-Zeilennumirung \(\tilde{A}\) bestimmt und anschließend in
eine positive \(\tilde{A_+}\) und negative \(\tilde{A_-}\) Matrix geteilt mit \(\tilde{A} = \tilde{A_+} - \tilde{A_-}\)(Jung et al., 2020).

Die zweite Phase ist die Iterationsphase:
In dieser Phase werden die Werte für \(r^{+}\) und \(r^{-}\) berechnet, dafür werden zwei Variabel \(\gamma , \beta\) zum ausbalancieren und eine Errortolleranz \(\epsilon\) eingeführt.
Zum Beginn dieser Phase wird der Startvektor q von dem Startknoten s gesetzt sowie \(r^{+} = q\) und \(r^{-} = 0\). Darauf folgt der iterative Teil in dem \(r^{+}\) und \(r^{-}\) immer wieder neu berechnet werden worauf ein h mit Hilfe einer vertikalen Verbindung von \(r^{+}\) und \(r^{-}\) berechnet wird. Dieses h wird mit dem h’(dem h aus der Iteration bevor) verglichen und wenn das Ergebnis schlechter als die vorgegebene Errortolleranz ist wird die Iteration beendet und ein \(r = r^{+} - r^{-}\) ausgegeben.

SRWR-PREP
Der SRWR-PREP ist eine Variante zur schnellen Findung von Ergebnissen für r. Vor allem der tausch von Startknoten kann sehr aufwändig werden.
Die Idee ist eine Berechnung von Werten ohne Iterationen. Auch diese Variante arbeitet in zwei Phasen:
Die Preprocessingphase:
In dieser Phase wird der gegebene gewichtet Graph in mehrere Untergraphen überführt, die in der Queryphase als Eingabe benötigt werden.
Zu Beginn wird A mit der hub, spoke Methode neugeordnet, sodass A einfach zu invertieren ist. Und dann werden wie im SRWR-ITER \(\tilde{A_+}\) und \(\tilde{A_-}\) berechnet.
Aus diesen Werten berechnen wir ein \(\vert H\vert = I - (1-c)(\tilde{A_+}^T + \tilde{A_-}^T)\) und ein \(T =I - (1-c)(\gamma \tilde{A_+}^T - \beta \tilde{A_-}^T)\).
\(\vert H\vert\) und T werden unterteilt in \(\vert H\vert_{11}\), \(\vert H\vert_{12}\), \(\vert H\vert_{21}\), \(\vert H\vert_{22}\) und \(T_{11}\), \(T_{12}\),
\(T_{21}\), \(T_{22}\) und berechnen jeweils \(\vert H\vert^{-1}_{11}\) und \(T^{-1}_{11}\).
Im nächsten Schritt werden die Schur Komplimente gebildet mit \(S_{\vert H\vert}= \vert H\vert_{22} - \vert H\vert_{21} \vert H\vert^{-1}_{11} \vert H\vert_{12}\) und
\(S_T = T_{22} - T_{21} T^{-1}_{11} T_{12}\)
Als letzter Schritt werden die LU Faktoren invertiert: \(S^{-1}_{\vert H\vert} = U^{-1}_{\vert H\vert} L^{-1}_{\vert H\vert}\), \(S^{-1}_{T} = U^{-1}_{T} L^{-1}_{T}\).
Und damit haben wir geeignete Teilmatrizen für den zweiten Teil des SRWR-PREP Algorithmuses mit \(U^{-1}_{\vert H\vert}, L^{-1}_{\vert H\vert} ,\vert H\vert^{-1}_{11},\vert H\vert_{12}\) und \(\vert H\vert_{21}\) aus \(\vert H \vert\) und \(U^{-1}_{T}, L^{-1}_{T},T^{-1}_{11} ,T_{12}\) und \(T_{21}\) aus T.

Die Queryphase
In dieser Phase wird aus den gegebenen Teilmatrizen die Vertrauenswerte \(r^+\) und \(r^-\) für einen Startknoten s berechnet.
Zuerst wird ein Vektor q erstellt der nur für den Startknoten den Wert 1 und sonst 0 einnimmt, q wird dann in \(q_1\) und \(q_2\) aufgeteilt.
Im nächsten Schritt werden \(p_1\) und \(p_2\) und aus dessen Verbindung p bestimmt mit:
\(p_2 = c(S^{-1}_{\vert H\vert}(q_2 -\vert H\vert_{21}(\vert H\vert^{-1}_{11}(q_1))))\) und
\(p_1 = \vert H\vert^{-1}_{11}(c q_1 - \vert H\vert_{12}p_2)\)
Damit berechnet man ein \(t = \tilde{A_-}^T p\) und teilt diese T wieder in ein \(t_1\) und \(t_2\) auf.
Zur Bestimmung von \(r^-\) wird nun \(r^-_1\) und \(r^-_2\) berechnet:
\(r^-_2 = (1-c)(S^{-1}_T(t_2 - T_{21}(T^{-1}_11(t_1))))\) und
\(r^-_1 = T^{-1}_{11}((1-c)t_1 - T_{12}r^-_2)\)
Aus \(r^-\) und \(p\) können wir \(r^+ = p - r^-\) berechnen und damit liefert der Algorithmus ein \(r\) aus \(r = r^+ - r^-\).
Das heißt mit dieser Variante können wir schnell eine Idee für den Vertrauenswert für verschiedene Konten gewinnen.

4.Evaluierung und Experimente des Algorithmuses
4.1 Vergleich SRWR und RWR
Wir vergleichen die Ergebnisse der SRWR und RWR anhand der folgenden Beispiele:
1.Ein Teilgraph der Slashdot dataset, der nur positiven Kanten enthält (Knoten 0 bis 20)
2.Ein Teilgraph der Slashdot dataset, der gemischte negative und positive Kanten enthält (Kanten 0 bis 40)
Zu erwähnen ist allerdings, dass wir bei dem zweiten Beispiel für RWR die negativen Kanten aus dem Graph entfernt haben. Deshalb kann man nicht davon ausgehen, dass es sich um zwei ganz identischen Graphen handelt.
Die verwendeten Parameter sind c=0.15, \(\epsilon\)=1e-9, \(\beta\)=0.5, \(\gamma\)=0.5.
1.Ein Teilgraph mit nur positiven Kanten:
| Knoten | SRWR | RWR |
|---|---|---|
| 0 | 3.809472e-01 | 3.809472e-01 |
| 1 | 1.619025e-02 | 1.619026e-02 |
| 2 | 1.619025e-02 | 1.619026e-02 |
| 3 | 5.023289e-02 | 5.023290e-02 |
| 4 | 2.077749e-02 | 2.077750e-02 |
| 5 | 1.963068e-02 | 1.963069e-02 |
| 6 | 1.619025e-02 | 1.619026e-02 |
| 7 | 1.619025e-02 | 1.619026e-02 |
| 8 | 6.553762e-02 | 6.553763e-02 |
| 9 | 7.667902e-02 | 7.667902e-02 |
| 10 | 2.815696e-02 | 2.815697e-02 |
| 11 | 1.619025e-02 | 1.619026e-02 |
| 12 | 1.619025e-02 | 1.619026e-02 |
| 13 | 1.619025e-02 | 1.619026e-02 |
| 14 | 1.619025e-02 | 1.619026e-02 |
| 15 | 3.287634e-02 | 3.287634e-02 |
| 16 | 1.619025e-02 | 1.619026e-02 |
| 17 | 1.077705e-01 | 1.077706e-01 |
| 18 | 2.733165e-02 | 2.733165e-02 |
| 19 | 2.815696e-02 | 2.815697e-02 |
| 20 | 1.619025e-02 | 1.619026e-02 |
Hier sieht man gut, dass die Ergebnisse von RWR und SRWR bis mindestens. 5 stelle gleich sind. Die Ergebnisse sind identisch, da die Ungenauigkeit ab 5. Stelle mit Ungenauigkeiten beim Rechnen mit float-Werte zu erklären sind. SRWR und RWR liefern identische Ergebnisse, wenn der Graph keinen negativen Kanten enthält.
2.Teilgraph mit gemischten Kanten:
| Knoten | SRWR | RWR |
|---|---|---|
| 0 | 3.959041058911486610e-01 | 3.907254e-01 |
| 1 | 1.175854169361516093e-02 | 1.383819e-02 |
| 2 | 1.175854169361516093e-02 | 1.383819e-02 |
| 3 | 3.085248101643757457e-02 | 3.664979e-02 |
| 4 | 1.427364274132391156e-02 | 1.677881e-02 |
| 5 | 1.427364274132391156e-02 | 1.677881e-02 |
| 6 | 1.175854169361516093e-02 | 1.383819e-02 |
| 7 | 1.175854169361516093e-02 | 1.383819e-02 |
| 8 | 4.230824897967594422e-02 | 5.099944e-02 |
| 9 | 4.774719966707474672e-02 | 5.655818e-02 |
| 10 | 1.719954088323734018e-02 | 2.019026e-02 |
| 11 | 1.175854169361516093e-02 | 1.383819e-02 |
| 12 | 1.175854169361516093e-02 | 1.383819e-02 |
| 13 | 1.175854169361516093e-02 | 1.383819e-02 |
| 14 | 1.175854169361516093e-02 | 1.383819e-02 |
| 15 | 1.582694660082479762e-02 | 1.859219e-02 |
| 16 | 1.175854169361516093e-02 | 1.383819e-02 |
| 17 | 7.676478345997791997e-02 | 9.168632e-02 |
| 18 | 1.777104584109039445e-02 | 2.106311e-02 |
| 19 | 1.910698127261850968e-02 | 2.241905e-02 |
| 20 | 1.175854169361516093e-02 | 1.383819e-02 |
| 21 | 1.175854169361516093e-02 | 1.383819e-02 |
| 22 | 1.719954088323734018e-02 | 2.019026e-02 |
| 23 | 1.175854169361516093e-02 | 1.383819e-02 |
| 24 | 1.175854169361516093e-02 | 1.383819e-02 |
| 25 | -1.168592331333961204e-02 | 0.000000e+00 |
| 26 | -1.175854169361516093e-02 | 0.000000e+00 |
| 27 | -1.175854169361516093e-02 | 0.000000e+00 |
| 28 | -1.175854169361516093e-02 | 0.000000e+00 |
| 29 | -1.427364274132391156e-02 | 0.000000e+00 |
| 30 | 1.034743145120747138e-02 | 1.238694e-02 |
| 31 | 1.299715378813615617e-02 | 1.522966e-02 |
| 32 | 9.706884212704052113e-04 | 1.160572e-03 |
| 33 | 5.451850645009909471e-03 | 6.407811e-03 |
| 34 | 8.004877236158467217e-04 | 9.571728e-04 |
| 35 | 8.004877236158467217e-04 | 9.571728e-04 |
| 36 | 1.388192289896302695e-02 | 1.654385e-02 |
| 37 | 8.004877236158467217e-04 | 9.571728e-04 |
| 38 | 8.004877236158467217e-04 | 9.571728e-04 |
| 39 | 8.004877236158467217e-04 | 9.571728e-04 |
| 40 | 8.004877236158467217e-04 | 9.571728e-04 |
Beide Varianten von Random Walk with restart verhalten sich auch bei dem Graph mit gemischten Kanten ähnlich. Der Startnote hat immer den größten Vertrauenswert r. Obwohl die beiden r-Vektoren unterschiedliche r-Werte haben, stehen sie aber im gleichen Verhältnis zueinander. In dem Beispiel bedeutet es, wenn \(r_{33}\) kleiner ist als \(r_{34}\) beim SRWR, dann ist auch beim RWR \(r_{33}\) kleiner als \(r_{34}\). Außerdem fallen die r-Werte beim SRWR kleiner als RWR, wenn negative Kanten im Graph vorgekommen sind, da die negativen Kanten die Vertrauenswerte dämpfen, weil der Surfer bei negativen Kanten seinen Vorzeichen ändert und auf dem Lauf über diese negative Kante den r- Vektoren erhört. Da gibt es ab der negativen Kante den Fall „Freund von Feind“.
Hier kann man zusammenfassen, dass SRWR ein realistischeres Bild von dem Netzwerk darstellt. In dem Fall ignoriert RWR alle „Feind von Freund“-, „Freund von Feind“- und „Feind von Feind“- Fälle. Den verwendeten Code können sie hier finden.
4.1 Beispiel SRWR
Beispielgraph:
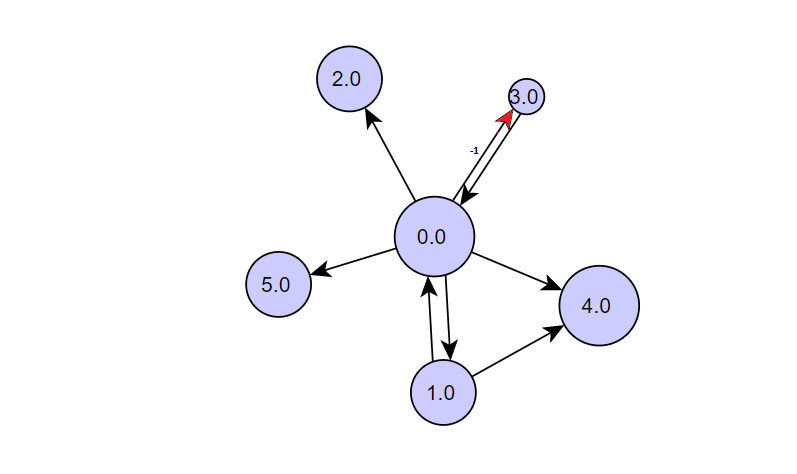
Wir begleiten ein Beispiel durch SRWR-ITER. Betrachten wir die gewichteten Kantenmatrix:
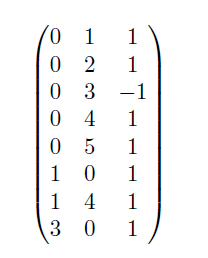
Erst erzeugen wir aus dieser Input-Matrix die Adjazenz Matrix A:
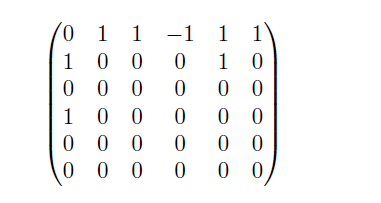
Wir geben A in den Normalisierungsalgorithmus und wir berechnen zuerst \(D^{-1}\):

Dann berechnen wir aus \(D^{-1}\) und A die Semi-row-normilized-matrix \(\tilde{A}\):

Weiter Teilen wir \(\tilde{A}\) in \(\tilde{A}_+\) und \(\tilde{A}_-\):
\(\tilde{A}_+\):

\(\tilde{A}_-\):
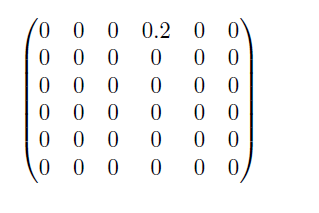
Hier sind wir mit der Normalisierung fertig. Im SRWR-ITER initialisierten wir \(r_+\) und \(r_-\) mit Nullen und setzten \(r_+\) an der Stelle der Startknoten mit 1 also:
\[r_+ = (1, 0, 0, 0, 0, 0)\] \[r_- = (0, 0, 0, 0, 0, 0)\]Weiter werden wir mit \(r_+\) und \(r_-\) und anderen Startparamter (c=0.15, \(\epsilon\)=1e-9, \(\beta\)=0.5, \(\gamma\)=0.5) in den rekursiven Formen einsetzen. Wir wiederholen diesen Teil und berechnen in jedem Schritt H‘ und berechnen den Fehler zwischen H(vom letzten Schritt) und H‘. Wir brechen ab, sobald der Fehler das \(\epsilon\) erreicht oder wir eine festgesetzte maximale Iterationsanzahl (in unserem Fall 300) erreicht haben. Bei diesem Beispiel erreichen wir \(\epsilon\) an 76. Iteration und brechen hiermit ab. Abschließend berechnen wir aus \(r_+\) und \(r_-\) Vektor den r.
Vertrauenswert r:
| Knoten | r |
|---|---|
| 0 | 4.463850822392118611e-01 |
| 1 | 8.2161746103442258378e-02 |
| 2 | 8.2161746103442258378e-02 |
| 3 | -8.2161746103442258378e-02 |
| 4 | 1.184141982140466953e-01 |
| 5 | 8.2161746103442258378e-02 |
5. Schlussfolgerung
Das Ziel der Arbeit ist Signed Random Walk with Restart, der personalisierte Vertrauensverhältnisse herausfinden kann, vorzustellen und ihn mit dem Vorgängermodell(RWR) zu vergleichen. Der Algorithmus hat eine iterative und eine preprocessing Variante, wobei der iterative Algorithmus nicht als Endprodukt geeignet ist, da der SRWR-PRE die Ergebnisse viel effizienter berechnen kann. Im Allgemeinen haben wir gezeigt, dass sich der SRWR auf Graphen ohne negativen Kanten immer noch gleich verhält im Vergleich zum RWR. Selbst wenn negative Beziehungen vorhanden sind, bleibt das Verhältnis zwischen den Ergebnissen gleich. Allerdings haben die negativen Kanten einen dämpfenden Einfluss auch auf positive Vertrauenswerte. Daher ist der SRWR eine verallgemeinerte Version vom RWR und gibt gleichzeitig realitätsnähere Ergebnisse.
6.Referenzen
- Jung, J., Jin, W., & Kang, U. (2020). Random walk-based ranking in signed social networks: model and algorithms. Knowledge and Information Systems, 62(2), 571–610. https://doi.org/10.1007/s10115-019-01364-z
- Backstrom, L., & Leskovec, J. (2011). Supervised random walks: predicting and recommending links in social networks. In I. King, W. Nejdl, & H. Li (Eds.), WSDM 2011 Hong Kong (pp. 635–644). ACM.
- Yin, X., Hu, X., Chen, Y., Yuan, X., & Li, B. (2019). Signed-PageRank: An Efficient Influence Maximization Framework for Signed Social Networks. IEEE Transactions on Knowledge and Data Engineering, 1. https://doi.org/10.1109/TKDE.2019.2947421
IV. J. Leskovec, D. Huttenlocher, J Kleinberg: Signed Networks in Social Media. 28th ACM Conference on Human Factors in Computing Systems (CHI), 2010.
