Spectral Clustering
| Rene Evertz | Sven Büge |
| RWTH Aachen University | RWTH Aachen University |
| rene.evertz@rwth-aachen.de | sven.buege@rwth-aachen.de |
Abstract
Seit einiger Zeit existiert das Interesse, Datensätze in kleinere Gruppen zu unterteilen, sie zu Clustern, um die Datensätze leichter auszuwerten oder zu verarbeiten. Die Anforderung an die für diesen Zweck eingesetzten Cluster-Alogrithmen sind Schnelligkeit, Zuverlässlichkeit und Konstanz. Mit steigender Größe und Komplexität der Datensätze, wird es zunehmend schwerer den Anforderungen gerecht zu werden und komplexe Strukturen aus den Datensätzen zu erkennen. Wir haben untersucht, wie Spectral Clustering funktioniert und sich in den benannten Belangen schlägt. Spectral Clustering kann aufgrund seiner Vielseitigkeit die meisten Datensätze erfolgreich clustern, jedoch benötigt es einiges an Erfahrung, um die besste Art des Spectral Clustering oder der benötigten Parameter auszuwählen, da noch keine bewiesenen allgemeingültigen Vorgehensweisen existieren, sondern nur ungefähre Vorgehensweisen. Es benötigt Forschung, um diese Beweise zu finden.
1. Einleitung
In unserer heutigen Zeit wird der Austausch von Informationen immer mehr digitalisiert. Aufgrund der menschlichen Verlustangst wurden alle als relevant angesehenen Informationen gespeichert.
Weiterhin ermöglichte die rasante Weiterentwicklung der Computer die Verarbeitung dieser riesiger Datenmengen. Das eröffnete die Möglichkeit, riesige Datenmengen auszuwerten.
Eine Auswertungsart dieser riesigen Datenmenge ist die Gruppenbildung in sozialen Netzwerken. Mithilfe solcher Auswertungen können beispielsweise Empfehlungssysteme erstellt oder Experten identifiziert werden.
Die Auswertung erfolgt per Cluster-Algorithmen.
Einer dieser Cluster-Alorithmen ist Spectral Clustering.
Die Idee des Spectral Clusterings entstand in den 1970er durch W.E.Donath und A.J.Hoffman (1973)(Donath & Hoffman, 2003) und M.Fiedler (1973)(Fiedler, 1973), die die Eigenschaften von Laplace-Matrizen und ihren Eigenvektoren untersuchten.
Dies wurde zu der Zeit jedoch nicht beachtet.
Anfang der 2000er wurde die Idee des Spectral Clusterings in leicht verändertert Form aufgegriffen (Shi & Malik, 2000), (Meila & Shi, 2001), (Ng et al., 2002).
Man benutzte anstatt der unnormalisierten Laplace-Matrix die normalisierte. Im folgenden stieg der Bekanntheitsgrad vom Spectral Clustering und es wird heutzutage häufig angewendet.
Da noch nicht alle Unwissenheiten ums Spectral Clusterings beseitigt wurden, wird immernoch aktiv daran geforscht.
Im Rahmen “Algorithmen für die Entdeckung von Communities in sozialen Netzwerken” untersuchen wir Spectral Clustering auf die dahinterstehende Theorie, wie ein Algorithmus funktioniert,
wie leicht sich Spectral Clustering anwenden lässt und wie gut es sich für den gegebenen Anwendungsbereich eignet.
2. Verwandte Arbeiten
Diese Paper basiert zu größten Teilen auf der Arbeit “A Tutorial on Spectral Clustering” von Ulrike von Luxburg(Von Luxburg, 2007).
3. Theorie Spectral Clustering
Ist eine Sammlung an Datenpunkten \(x_{i}, ... ,x_{n}\) gegeben, die über Ähnlichkeitswerte \(s_{ij}\) miteinander verbunden sind, so möchte man Gruppen bilden, in denen die Punkte innerhalb einer Gruppe durch hohe Ähnlichkeitswerte verbunden sind, jedoch eine geringe Verbindung zu Punkten aus anderen Gruppen haben. Um besser mit den Datenpunkten arbeiten zu können, notieren wir diese als Graphen \(G=(V,E)\). Dieser Graph \(G\) besitzt die Knoten \(v_{i}\), von denen jeder einen Datenpunkt \(x_{i}\) repräsentiert. Kanten von verbundnenen Knoten \(v_{1}\) und \(v_{j}\) werden mit den Ähnlichkeitswerten \(s_{ij}\) gewichtet, daher nennen wir den Graph Ähnlichkeitsgraph. Möchte man nun diesen Ähnlichkeitsgraphen in Gruppen unterteilen, so sollten die Kanten zwischen verschienenen Gruppen ein niedriges Kantengewicht haben, also möglichst unterschiedlich zueinander sein, und Kanten innerhalb einer Gruppe ein hohes Kantengewicht haben, also möglichst ähnlich zueinander sein. Um im Verlauf dieses Papers besser mit diesen Graphen zu arbeiten, legen wir im Folgenden einige Graphennotationen fest.
Graphennotation
Sei \(G=(V,E)\) ein ungerichteter Graph mit der Menge an Knoten \(V={v_{1}, ... ,v_{n}}\). Die Kanten des Graphen sind nicht negativ gewichtet. Sind die Knoten \(v_{i}\) und \(v_{j}\) mit einer Kante verbunden, so trägt diese das Gewicht \(w_{ij} \ge 0\). Daraus wird die gewichtete Adjazenzmatrix \(W=(w_{ij})_{i,j=1,...,n}\) gebildet. Existiert keine Kante zwischen zwei Knoten \(v_{i}\) und \(v_{j}\) so ist \(w_{ij}=0\). Da G ungerichtet ist, gilt \(w_{ij}=w_{ji}\). Der Grad eines Knoten \(v_{i} \in V\) ist definiert als \(d_{i}= \sum\limits_{j=1}^n {w_{ij}}\), die Summe der Gewichte aller Kanten, die an \(v_{i}\) anliegen. Die Grad-Matrix ist eine Diagonalmatrix mit den Einträgen \(d_{ii}=d_{i}\) und \(d_{ij}=0\) für \(i \neq j\). Das Komplement \((V \setminus A)\) einer Untergruppe \(A \subset V\) wird als \(\bar{A}\) geschrieben. Wir definieren den zu \(A\) gehörigen Inzidenzvektor \(i_{A}=(f_{1},...,f_{n})^t \in R^n\) mit den Einträgen \(f_{i}=x,x=konst.,x \neq 0\) falls \(v_{i} \in A\) ist, ansonsten \(f_{i}=0\).
Die nicht leeren Teilmengen \(A_{1},...,A_{k}\) bilden eine Partition, wenn \(A_{i}\) und \(A_{j}\) disjunkt sind und die Vereinigung von \(A_{i},...,A_{j}=V\) ist. Eine Untergruppe A heißt zusammenhängend, falls es zwischen den Knoten \(v_{i}\) und \(v_{j}\) einen Weg gibt, der ausschließlich Knoten aus \(A\) enthält. Außerdem heißt eine Untergruppe \(A\) Zusammenhangskomponente, wenn kein Knoten \(v_{i} \in A\) mit einem Knoten \(v_{j} \in \bar{A}\) verbunden ist.
Erstellung Ähnlichkeitsmatrix
Damit die Datenpunkte \(x_{i}, ... ,x_{n}\) verwendet werden können, müssen sie in einen Ähnlichkeitsgraphen umgeformt werden. Für diese Umformung gibt es vier häufig benutzte Vorgehensweisen. Hier sollte man beachten, dass die Datenpunkte entweder durch Ähnlichkeitswerte \(s_{ij}\) verbunden sein können, oder durch ihre Entfernung zueinander. Welche der folgenden Methoden sich am besten eignet erläutern wie im Punkt Anwendung.
\(\epsilon\)-Nachbarschaftsgraph
Zuerst wird ein \(\epsilon\) gewählt. Als nächstes werden alle Kanten miteineander verbunden, deren Ähnlichkeitswert größer \(\epsilon\) ist, bzw. deren Distanz zueinander kleiner als das dementsprechend gewählte \(\epsilon\) ist. Da nun die Kantengewichte sich ungefähr in der selben Größenordnung \(\epsilon\) befinden, kann man alle Kanten mit 1 gewichten. Tut man dies nicht so sei zu beachten, dass im Falle von mit der Distanz gewichteten Kanten, diese Gewichte in Ähnlichkeitswerte umgeformt werden müssen, da große Kantengewichte beim Spectral Clustering für eine starke Verbindung stehen.
K-Nächste-Nachbarn Graph (KNN Graph)
Hierbei schauen wir und die k nächsten Nachbarn eines Knoten \(v_{i}\) an, also die Knoten, mit denen \(v_{i}\) am stärksten verbunden ist, sprich die höchsten
Ähnlichkeitswerte bzw. niedrigsten Distanzen zu den benachbarten Knoten.
Es werden alle Knoten miteinander verbunden, für die gilt:
- \(v_{j}\) ist unter den k nächsten Nachbarn von \(v_{i}\)
- \(v_{i}\) ist unter den k nächsten Nachbarn von \(v_{j}\)
und den jeweiligen Kanten die entsprechenden Ähnlichkeitswerte zugewiesen. Man kann hier leicht sehen, dass jeder Knoten mindestens mit k anderen Knoten
verbunden ist.
gemeinsamer KNN Graph
Die Vorgehensweise entspricht der, des KNN Graphen, mit dem Unterschied, dass beide Bedingungen gelten müssen, damit Knoten \(v_{i}\) und \(v_{j}\) miteinander verbunden werden. Folglich sind Knoten maximal mit k anderen Knoten verbunden.
voll verbundener Graph
Es werden grundsätzlich alle Knoten miteinander verbunden und den Kanten wird ein Gewicht zugeteilt, welches durch eine Ähnlichkeitsfunktion ermittelt wird, wie zB. der gaußschen Ähnlichkeitsfunktion \(s(x_{i},x_{j})=exp(− \frac{‖xi−xj‖^2}{2 \sigma ^2})\), bei der das \(\sigma\) steuert, ab wann höhere Werte drastisch fallen. Die gußsche Ähnlichkeitsfunktion kann generell genutzt werden, um Distanzen in Ähnlichkeitswerte umzuwandeln.
Laplace-Matrix
Die Laplace-Matrix mit ihren Eigenschaften ist der Grund dafür, dass Spectral Clustering existiert. Da es verschiedene Arten von Laplace-Matrizen gibt, werden wir im folgenden zuerst die Laplace-Matrix definieren, von der wir sprechen und daraufhin ihre für Spectral Clustering wichtigen Eigenschaften darlegen.
unnormalisierte Laplace-Matrix
diese wird wiefolgt definiert: \(L=D-W\)
Die wichtigste Eigenschaft ist: \(f^tLf = \frac{1}{2} \sum\limits_{i,j=1}^n {w_{ij}(f_{i}-f_{j})^2}\)
Beweis:
\(f^tLf=f^tDf-f^tWf\)
Aufgrund der Definition von \(D\) können wir nun schreiben
\(= \sum\limits_{i=1}^n {d_{i}f_{i}^2} - \sum\limits_{i,j=1}^n {f_{i}f_{j}w_{ij}}\)
Wir verwenden quadratische Ergänzung und \(d_{i}= \sum\limits_{j=1}^n {w_{ij}}\)
\(= \frac{1}{2}( \sum\limits_{i=1}^n {( \sum\limits_{j=1}^n {w_{ij}})f_{i}^2} - 2 \sum\limits_{i,j=1}^n {f_{i}f_{j}w_{ij}} + \sum\limits_{j=1}^n {( \sum\limits_{i=1}^n {w_{ij}})f_{i}^2})\)
\(= \frac{1}{2}( \sum\limits_{i,j=1}^n {w_{ij}(f_{i}-f_{j})^2}\)
Daraus ist zu schließen, dass \(L\) positiv semidefinit ist(Von Luxburg et al., 2008). Da sowohl \(D\) als auch \(W\) per Definition Symmetrisch sind, ist \(L\) auch symmetrisch.
0 ist ein Eigenwert von \(L\), mit einem konstanten Eigenvektor, da die Summe jeder Reihe aus \(L=0\) ist, aufgrund der Definiton von \(D\) in abhängigkeit von \(W\).
Aus den vorherigen Eigenschaften lässt sich folgern, dass die Eigenwerte \(0 = \lambda_{1} \le \lambda_{2} \le ... \le \lambda_{n}\) sind.
Sei \(G\) ein ungerichteter Graph mit nicht-negativen Gewichten, dann entspricht die Anzahl der Eigenwerte 0 der Anzahl Zusammenhangskomponenten
\(A_{1},...,A_{k}\) im Graphen. Die zu diesen Eigenwerten dazugehörigen Eigenvektoren entspechen den Inzidenzvektoren von \(A_{1},...,A_{k}\).
Beweis:
Für \(k=1\):
Der Graph ist voll verbunden. Sei \(f\) der Eigenvektor mit dem Eigenwert 0.
Daraus folgt \(0=f^tLf = \frac{1}{2} \sum\limits_{i,j=1}^n {w_{ij}(f_{i}-f_{j})^2}\).
Da \(w_{ij} \ge 0\) und \((f_{i}-f_{j})^2\) sind, kann die Summe nur 0 ergeben, wenn alle Therme 0 ergeben. Sind \(v_{i}\) und \(v_{j}\) verbunden,
so muss \(f\) an der Stelle \(i=f_{j}\) sein.
Alle Knoten, die über Wege miteinander verbunden sind, müssen folglich den gleichen Eintrag in \(f\) haben. Da in einer Zusammenhangskomponente
alle Knoten über Wege miteinander verbunden sind, muss \(f\) über alle Einträge der entsperchenden Knoten konstant sein. Unter der Annahme \(k=1\)
sehen wir, dass alle Einträge in \(f\) in diesem Fall konstant sind.
Für \(k=x\) mit \(x \geq 2\):
Nehmen wir zur Verdeutlichung an, die Knoten seien den Zusammenhangskomponenten entsprechend angeordnet. In diesem Fall wird unsere Adjazenzmatrix
\(W\) blockdiagonal und dementsprechend wird das auch unsere Laplace-Matrix \(L\):
\(L =\) \(\left(\begin{matrix}L_{1} & & & \\ & L_{2} & & \\\ & & \ddots & \\ & & & L_{x}\end{matrix}\right)\)
Jeder Block ist eine Laplace-Matrix zu der entsprechenden Zusammenhangskomponente. Wie für alle Diagonalmatrizen gültig, besteht das Spektrum von \(L\)
aus der Vereinigung der Spektren von \(L_{i}\), und die dazugehörigen Eigenvektoren von \(L\) sind die Eigenvektoren von \(L_{i}\) mit 0 an den Stellen \(j\), mit\(j \in \bar{A}\),
den Inzidenzvektoren von \(A_{i}\). Da jedes \(L_{i}\) eine Laplace-Matrix zu einem voll verbundenen Graphen ist und vorher gezeigt wurde,
dass jede solcher Laplace-Matrizen den Eigenwert 0 genau einmal besitzt. Der dazugehörige Eigenvektor ist ein konstanter Vektor über die i-te
Zusammenhangskomponente.
Folgerlich hat eine Matrix \(L\) sooft den Eigenwert 0, wie es Zusammenhangskomponenten in \(G\) gibt und die dazugehörigen Vektoren sind Inzidenzvektoren der Zusammenhangskomponenten.
normalisierte Laplace-Matrix
Es gibt zwei häufig verwendete normalisierte Laplace-Matrizen, die verknüpfte Eigenschaften aufweisen.
symmetrische Laplace-Matrix \(L_{sym} := D^{- \frac{1}{2}}LD^{- \frac{1}{2}} = I - D^{- \frac{1}{2}}WD^{- \frac{1}{2}}\)
random Walk Laplace-Matrix \(L_{rw} := D^{-1}L = I - D^{-1}W\)
Es gilt: \(f^tL_{sym}f = \frac{1}{2} \sum\limits_{i,j=1}^n {w_{ij}} ( \frac{f_{i}}{\sqrt{d_{i}}} - \frac{f_{j}}{\sqrt{d_{j}}})^2\).
\(\lambda\) ist ein Eigenwert von \(L_{rw}\) mit dem Eigenvektor \(u\), genau dann wenn \(\lambda\) ein Eigenwert von \(L_{sym}\) ist, mit dem Eigenvektor \(w = D^{ \frac{1}{2}}u\)
Multipliziert man \(D^{- \frac{1}{2}}\) von links an die Eigenvektorgleichung \(L_{sym}w = \lambda w\), muss man nur noch \(D^{- \frac{1}{2}}w\) durch \(u\) ersetzen.
0 ist ein Eigenwert von \(L_{rw}\) mit einem konstanten Vektor \(f\) als Eigenvektor. 0 ist ein Eigenwert von \(L_{sym}\) mit dem Eigenvektor \(D^{ \frac{1}{2}}f\).
Aus diesen beiden Eigenschaften ist zu folgern, dass die Eigenwerte von \(L_{sym}\) und \(L_{rw}\) \(0 = \lambda_{1} \le \lambda_{2} \le ... \le \lambda_{n}\) sind.
Wie bei der unnormalisierten Laplace-Matrix ist die Anzahl der Eigenwerte 0 in Abhänigkeit der Zusammenhangskomponenten und die dazugehörigen
Eigenvektoren sind für \(L_{rw}\) die Inzidenzvekoren von \(A_{i}\), bei \(L_{sym}\) dementsprechend \(D^{\frac{1}{2}}f_{A_{i}}\).
Unnormalisierter Spectral Clustering Algorithmus
Als Eingabeparameter werden n Punkte \(x_{i},...,x_{n}\) und \(k\), die Anzahl der zu bildenen Gruppen übergeben.
- Bilde aus den Punkten \(x_{i},...,x_{n}\) einen Distanzgraphen.
- Reduziere den Graphen mithilfe der genannten Methoden.
- Erstelle eine Ähnlichkeitsmatrix aus dem Graphen.
- Berechne die unnormalisierte Laplace-Matrix (\(L = D - W\)).
- Berechne die \(k\) kleinsten Eigenvektoren von \(L\).
- Sei \(U \in R^{n \times k}\) die Matrix mit den Einheitsvektoren als Spalten aneinander gereiht.
- Sei \(y_{i} \in R^k\) mit \(i=1,...,n\) der Vektor, der der i-ten Zeile von \(U\) entspricht.
- Cluster die Koordinaten \((y_{i})_{i=1,...,n} \in R^k\) mit dem k-means oder ähnlichen Clusteralgorithmen
in k Gruppen \(C_{1},...,C_{n}\) und gib diese aus.
Auf den ersten Blick wirkt es komisch, dass man hier k-means anwendet, warum benutzt man nicht gleich k-means.
Stellen wir uns vor unser Graph besteht aus 3 Kreisen, ein großer, ein mittelgroßer und ein kleiner Kreis und diese liegen ineinander, sind aber nicht miteinander verbunden.
Nur k-means würde diesen Graphen, wie einen Kuchen, in drei ungefähr gleichgroße Gruppen unterteilen.
Gibt man jedoch k-means die Zeilen der Eigenvektormatrix als Eingabe, also wendet Spectral Clustering an, so wird k-means die einzelnen Kreise als Gruppen ausgeben.
Das liegt daran, dass die Eigenvektormatrix die Punkte in deutlichere Gruppen aufteilt, in unserem Beispiel werden Knoten aus der ersten Gruppe die Koordinaten \(\begin{pmatrix} x \\ 0 \\ 0 \end{pmatrix}\) haben,
die Knoten aus der zweiten Gruppe \(\begin{pmatrix} 0 \\ y \\ 0 \end{pmatrix}\) und die aus der dritten \(\begin{pmatrix} 0 \\ 0 \\ z \end{pmatrix}\) mit \((x,y,z \neq 0)\).
Wir wissen dies dank der beschriebenden Eigenschaften der Laplace-Matrix. Für k-means bereiten diese drei gebildeten Gruppen kein Problem mehr sie zu unterteilen und wir bekommen unser gewünschtes Ergebnis.
4. Anwendung
Nun schauen wir uns die Anwendung von Spectral Clustering auf 2-Dimensionalen Netzwerke an. Dazu haben wir das Programm “Spectral Visual” mittels C# entwickelt. Das Programm dient zu Erstellung/Laden von Datensätzen und zum Auswerten dieser Datensätze mittels Spectral Clustering Implementierung mittels Java.
Datensätze
Ein Datensatz besteht aus 3 Komponenten. Das ist zunächst der Name des Datensatzes. Weiterhin beinhaltet es die Konten und die gewichteten Kanten in Form einer Adjazenzmatrix. Datensätze können per Auswahl “Temp Daten” in der Datensatzauswahl erstellt werden. Hierzu öffnet sich ein neues Fenster “Graph Creator”, wo man auf einer Fläche mit 800x800 Pixeln Knoten einzeichnen kann. Beim Erstellen werden die Distanzen zwischen den Punkten berechnet und es wird die Adjazentmatrix gebildet.
Geeignete Auswahl der Parameter
Sobald ein Datensatz festgelegt ist, muss man nun geeignete Parameter finden. Diese Aufgabe ist fern weg von trivial. Spectral Clustering ist sehr flexibel, was auch zur Folge hat, dass eine schlechte Wahl von Parametern zu katastrophalen Ergebnissen führen kann.
Ähnlichkeitsfunktion
Der erste wichtige Parameter ist die Ähnlichkeitsfunktion selber. Sie soll Knoten, welche sich nah beeinander befinden, als möglichst ähnlich beschreiben. Beliebt ist hier die Gaussische Ähnlichkeitsfunktion \(s(x_{i},x_{j})=exp(− \frac{‖xi−xj‖^2}{2 \sigma ^2})\). Es lässt dich jedoch keine generel geeignete Auswahl treffen, da die Funktion vom Datensatz abhändig ist.
Graphreduzierungsart
Die nächste wichtige Entscheidung ist die Auswahl der Graphreduzierungsart. Wir schauen uns nun ein paar Beispiele an.
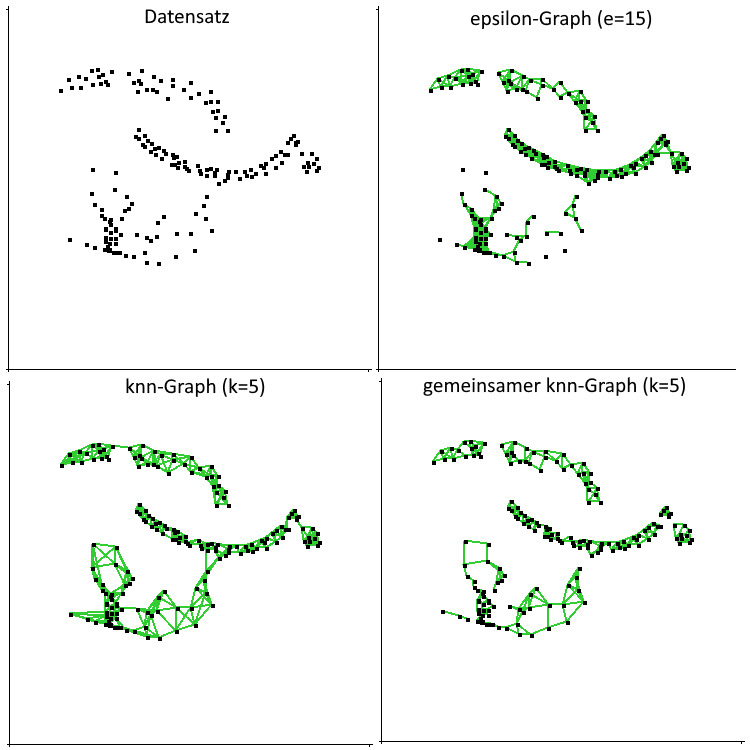 Abbildung 1: Verschiedene Graphreduzierungsarten
Abbildung 1: Verschiedene Graphreduzierungsarten
In Abbildung 1 sehen wir, dass verschiedene Verfahren zu verschiedenen Ergebnissen führen.
Beim \(\epsilon\)-Nachbarschaftsgraphen sehen wir, dass unten mehrere einzelne Punkte nicht verbunden sind. Das Problem mit dem \(\epsilon\)-Nachbarschaftsgraphen besteht darin, dass der Graph nicht mit verschiedenen Skalierungen auf dem Graph klar kommt.
Die KNN-Graphen kommen hingegen mit verschiedenen Skalierungen besser klar. Wir sehen, dass die einzelnen Punkte mit den restlichen Punkten verbunden sind. Das ist eine generelle und nützliche Eigenschaft von KNN-Graphen. Wir wollen uns nochmal an folgende Eigenschaft von KNN-Graphen erinnern: Jeder Knoten hat mindestens k Kanten.
Der gemeinsamen KNN-Graph hat die Eigenschaft, Knoten innerhalb von Bereichen mit hoher Dichte zu verbinden. Jedoch verbindet er keine Gruppen mit verschiedenen Dichten. Der gemeinsame KNN-Graph eignet sich daher zum Clustern von Gruppen mit unterschiedlichen Dichten.
Der vollverbundene Graph wird sehr häufig in Verbindung mit der Gausschen Ähnlichkeitsfunktion verwendet. Hier spielt der Parameter \(\sigma\) eine ähnliche Rolle zu dem \(\epsilon\) bei dem \(\epsilon\)-Nachbarschaftsgraphen. Hier haben Kanten in Gruppen hohe Werte, während weit entfernte Knoten zwar einen positiven, aber sehr kleinen Wert. Jedoch erhalten wir am Ende keinen reduzierten Graphen. Diese Methode ist nur auf Distanzmatrizen anzuwenden, da die Kantengewichte umgekehrt werden.
Abschließend raten wir, den KNN-Graphen zu verwenden. Er ist einfach zu verwenden, das Resultat ist eine reduzierte Adjazenmatrix und es hat weniger Parameter, als andere Graphen.
Geeignetes Sigma für die Ähnlichkeitsfunktion
Das \(\sigma\) in der gaußschen Ähnlichkeitsfunktion spielt eine ähnliche Rolle wie das \(\epsilon\). Es sollen starke Verbindungen zu den nächsten Nachbarn bestehen, während die Verbindungen zu Knoten aus anderen Gruppen gegen 0 gehen sollen. In der Praxis ist dies mit Distanzmatrizen als Eingabe schwer umzusetzen, da die Graphen unterschiedlich skaliert sein können und das \(\sigma\) dementsprechend angepasst werden muss. Für diese Anpassung haben wir jedoch keine allgemeingültige Formel bilden können.
Auswertung
Zum Auswerten haben wir unser Programm (“Spectral Visual”) verwendet. Schauen wir uns nun einige Beispielauswertung an.
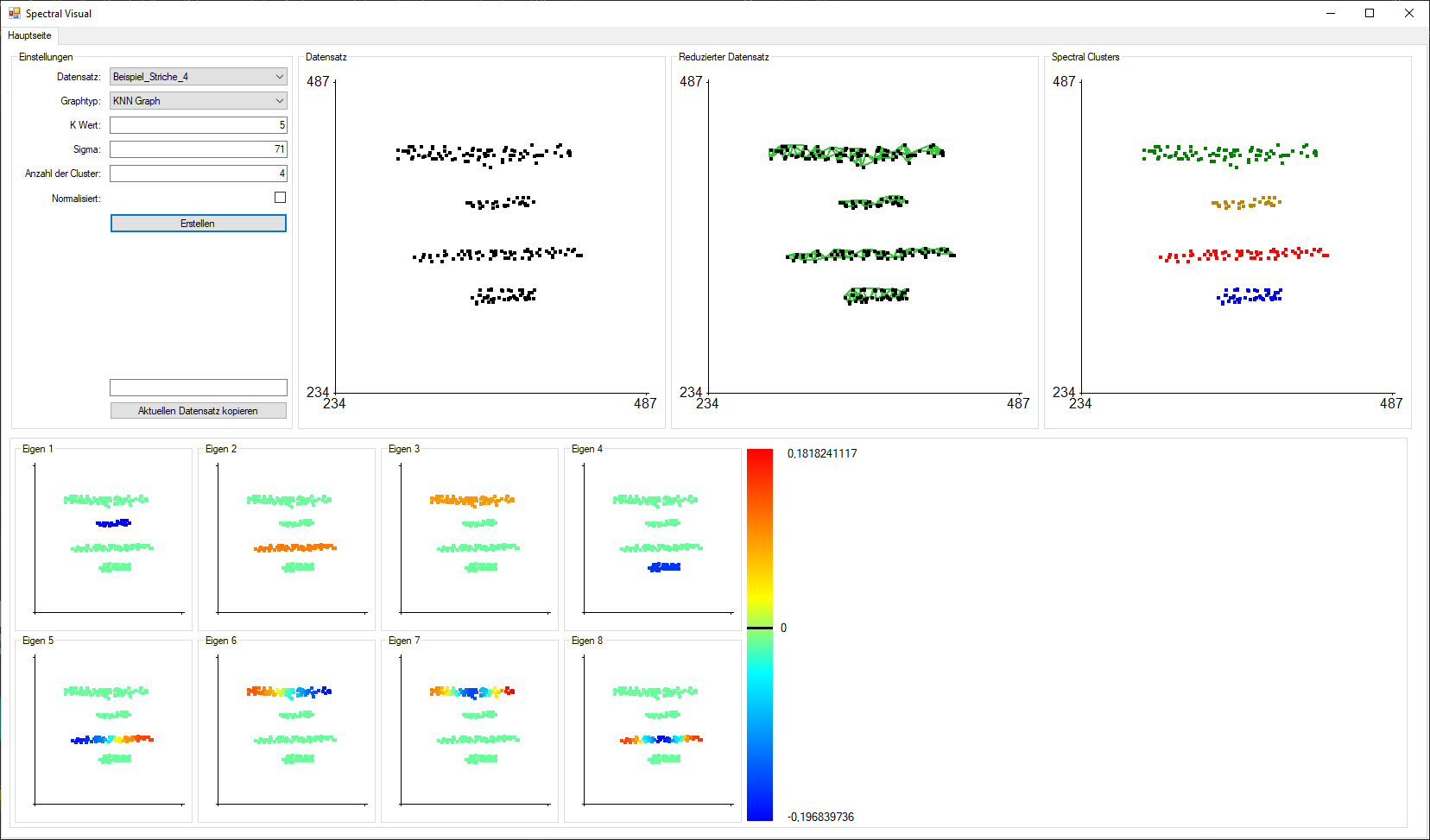 Abbildung 2: Spectral Visual(Graphtyp: KNN, K Wert: 5, Sigma: 71, Clusteranzahl: 4)
Abbildung 2: Spectral Visual(Graphtyp: KNN, K Wert: 5, Sigma: 71, Clusteranzahl: 4)
In Abbildung 2 sehen wir oben links die Einstellung der Auswertung. Auf dem Graph daneben befinden sich die Punkte des Datensatzes. Der Graph “Reduzierter Datensatz” zeigt alle Verbindungen, die nach der Graphreduzierung noch erhalten geblieben sind. Und ganz rechts sehen wir die Auswertung per Spectral Clustering. Unten links sieht man die Werte der 8 Eigenvektoren. Die i-ten Punktes steht für den i-ten Eintrag des Eigenvektors. Das Sigma wurde hier Pi Mal Daumen berechnet.
Hier sieht man auch deutlich, dass durch die Reduzierung vier Zusammenhangskomponenten entstanden sind. Das hat wie oben beschrieben die Folge, dass die ersten vier Eigenvektoren Inzidenzvektoren dieser vier Zusammenhangskomponenten sind. Das wird dadurch deutlich, dass jeweils eine Zusammenhangskomponente ungleich 0 ist und die Restlichen gleich 0.
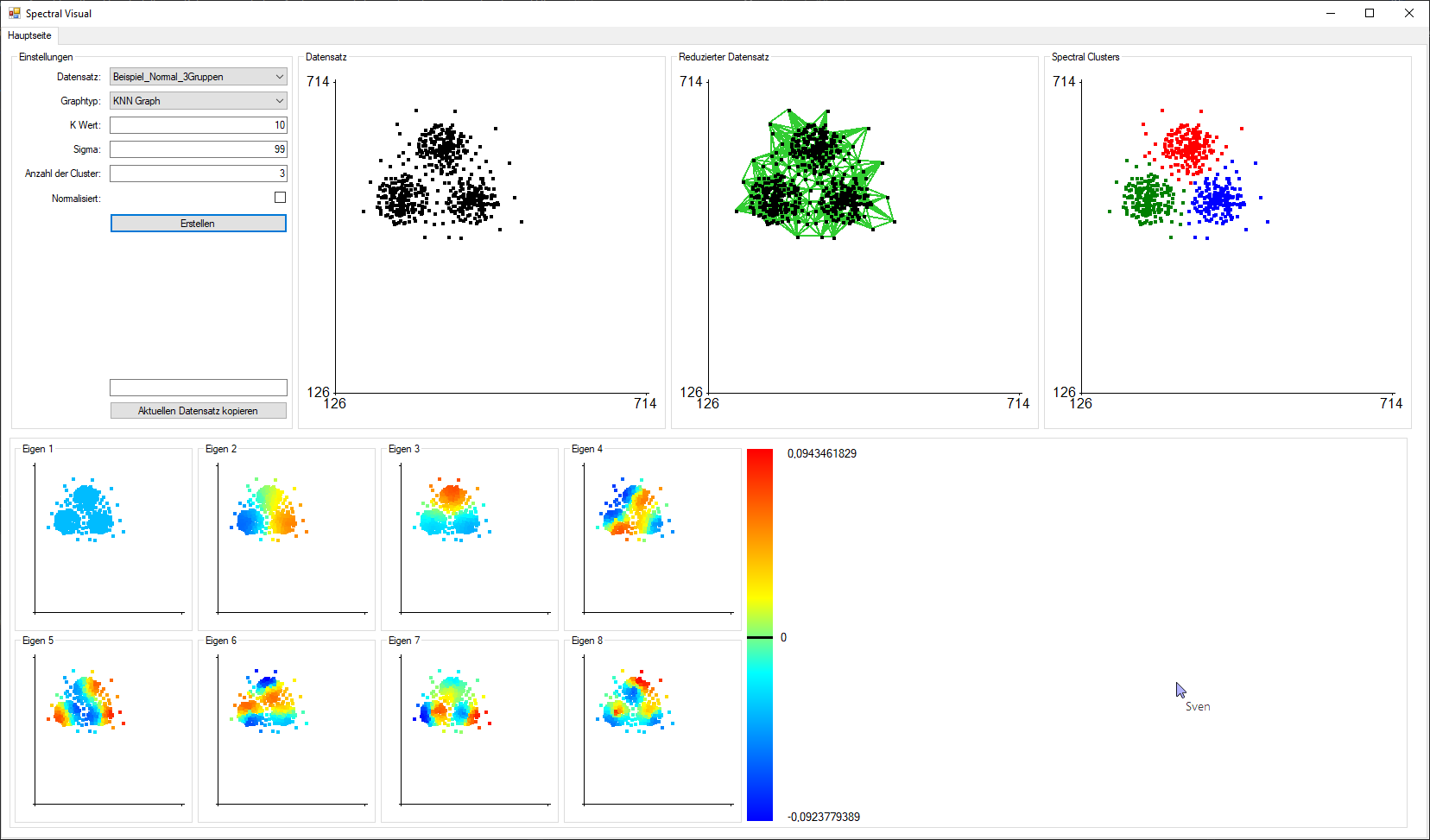 Abbildung 3: Spectral Visual(Graphtyp: KNN, K Wert: 10, Sigma: 99, Clusteranzahl: 3)
Abbildung 3: Spectral Visual(Graphtyp: KNN, K Wert: 10, Sigma: 99, Clusteranzahl: 3)
In Abbildung 3 betrachten wir nun einen Graphen, welcher aus einer Zusammenhangskomponente besteht. Hier sieht man, dass der erste Eigenvektor konstant ist. Beim zweiten kann man erkennen, dass die Gruppe unten rechts durch positive Werte hervorsticht und unten links durch negative. Beim dritten Eigenvektor trennt sich die obere Gruppe durch positive Werte vom Rest ab, welcher negative Werte besitzt.
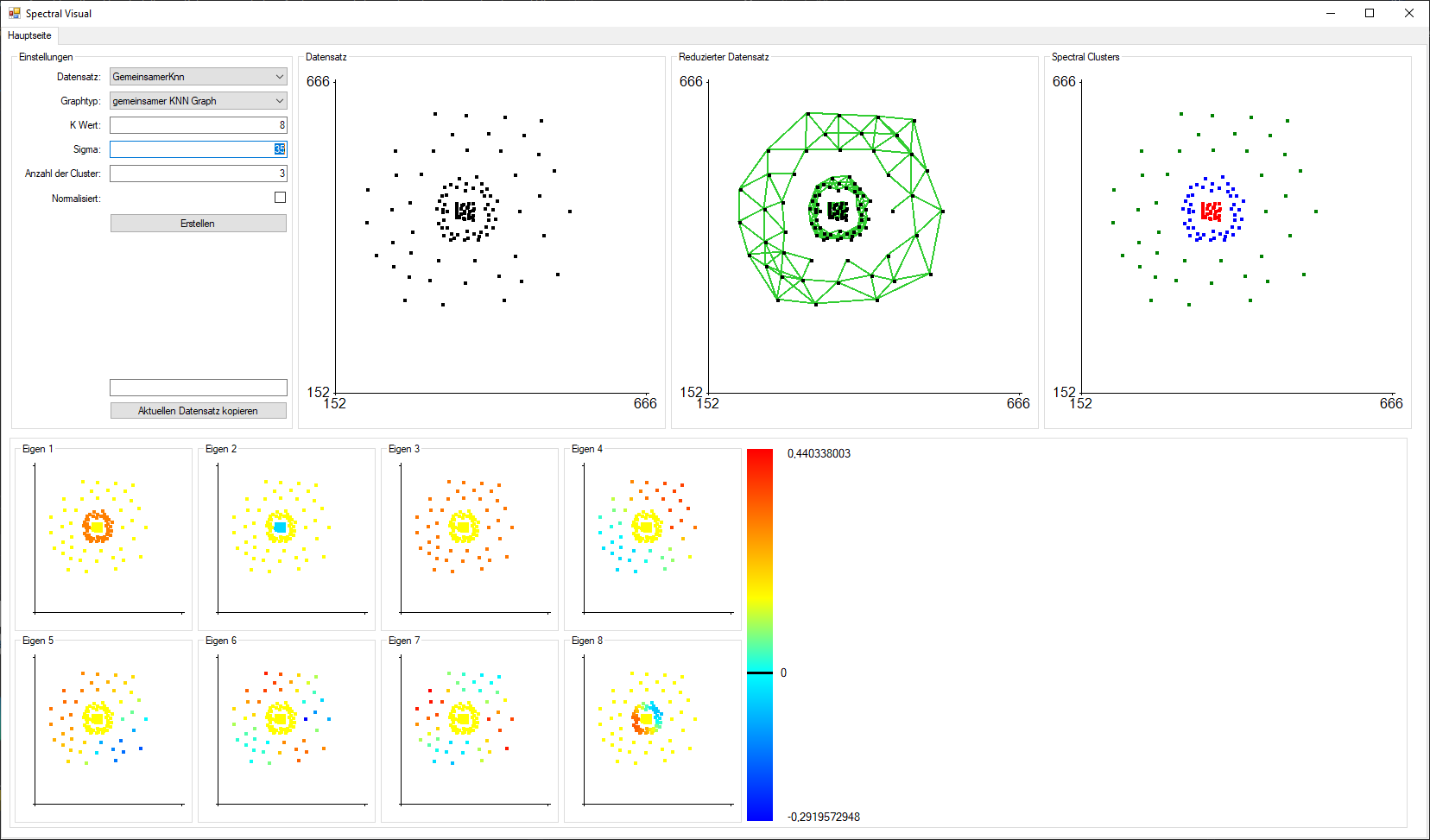 Abbildung 4: Spectral Visual(Graphtyp: GKNN, K Wert: 8, Sigma: 35, Clusteranzahl: 3)
Abbildung 4: Spectral Visual(Graphtyp: GKNN, K Wert: 8, Sigma: 35, Clusteranzahl: 3)
In Abbildung 4 wird mittels Gemeinsamer KNN nach der Dichte geclustert.
Hier sind noch ein paar Beispiele von den Möglichkeiten von Spectral Clustering.
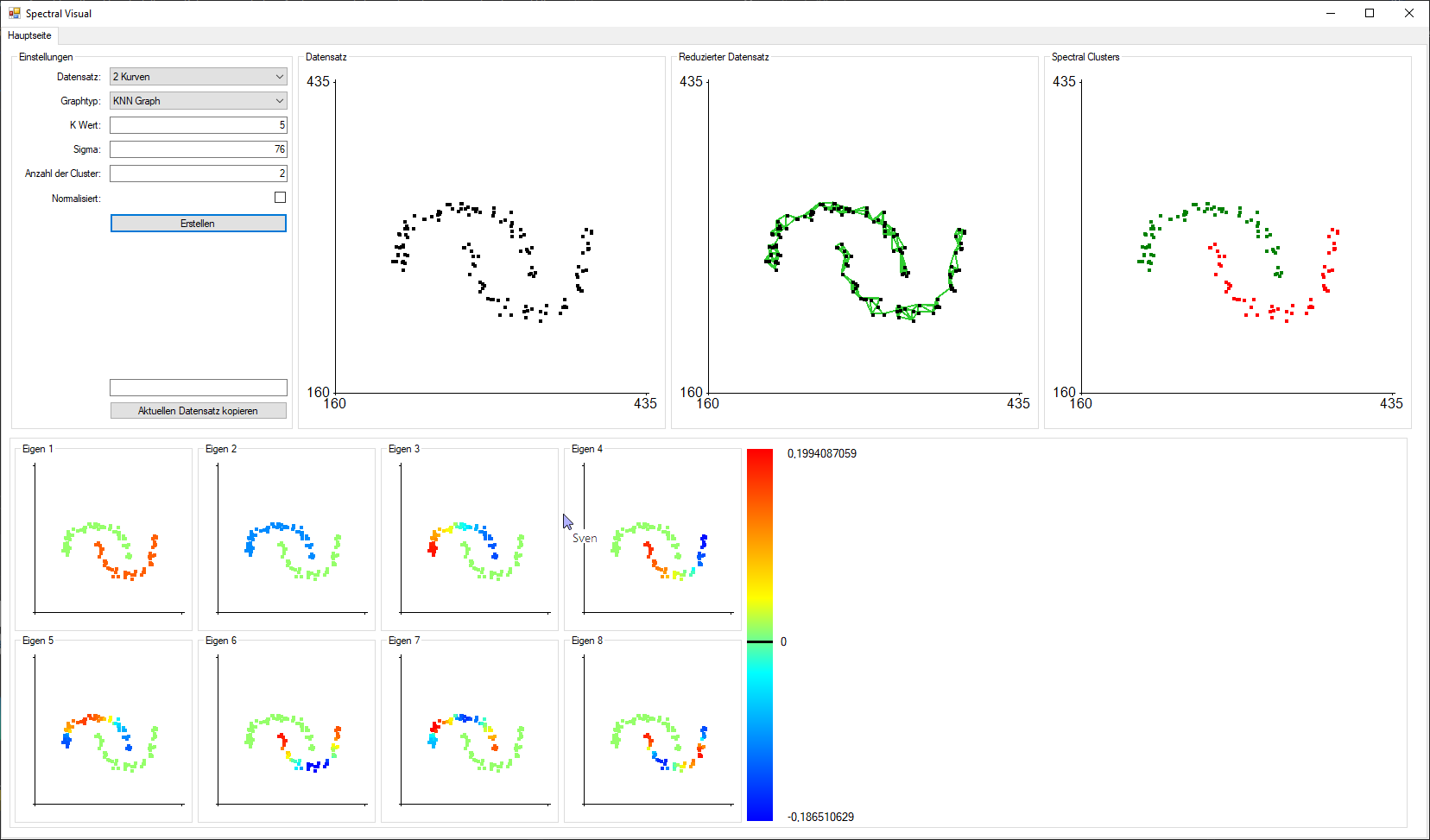 Abbildung 5: Spectral Visual(Graphtyp: KNN, K Wert: 5, Sigma: 76, Clusteranzahl: 2)
Abbildung 5: Spectral Visual(Graphtyp: KNN, K Wert: 5, Sigma: 76, Clusteranzahl: 2)
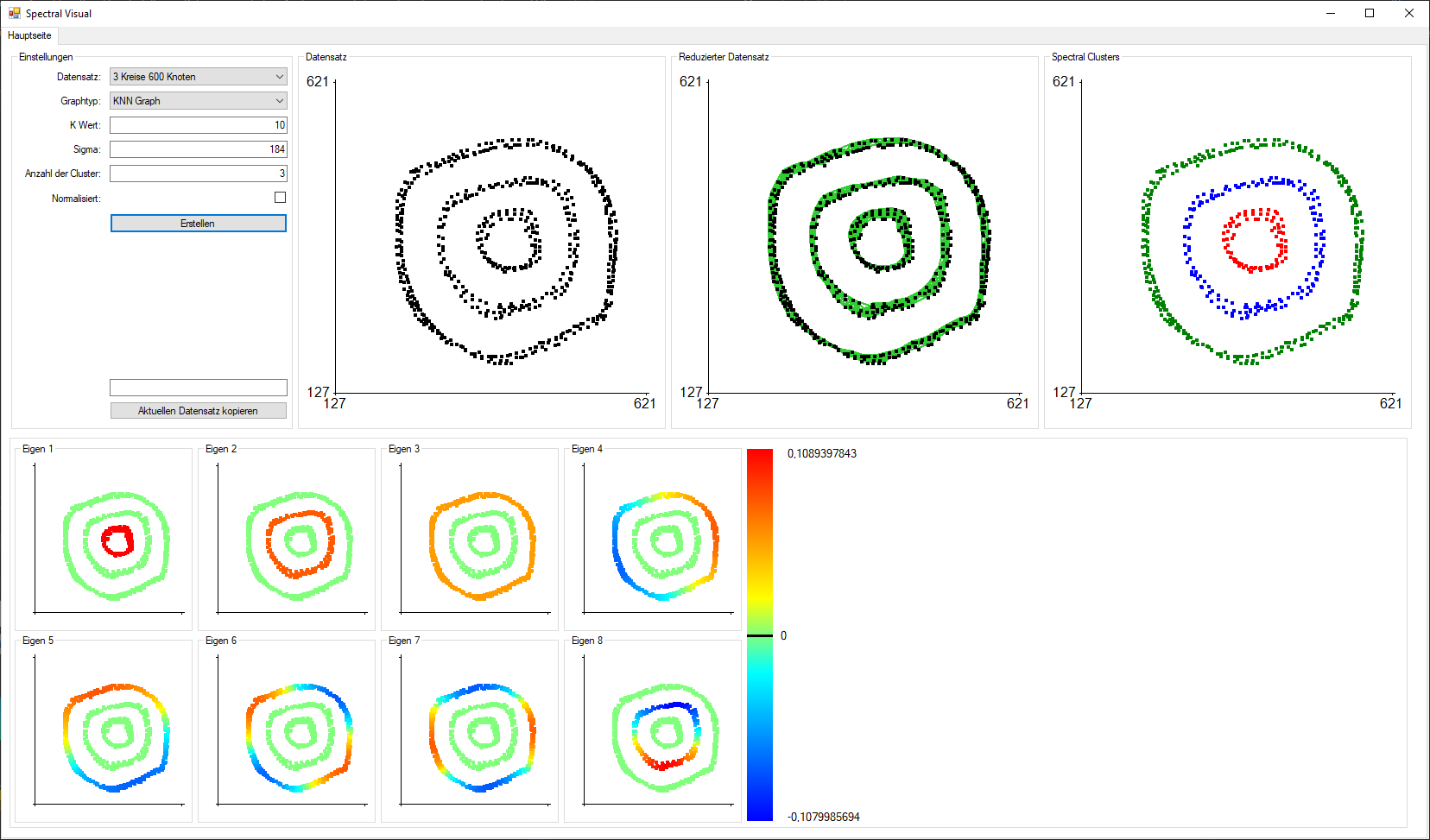 Abbildung 6: Spectral Visual(Graphtyp: KNN, K Wert: 10, Sigma: 184, Clusteranzahl: 3)
Abbildung 6: Spectral Visual(Graphtyp: KNN, K Wert: 10, Sigma: 184, Clusteranzahl: 3)
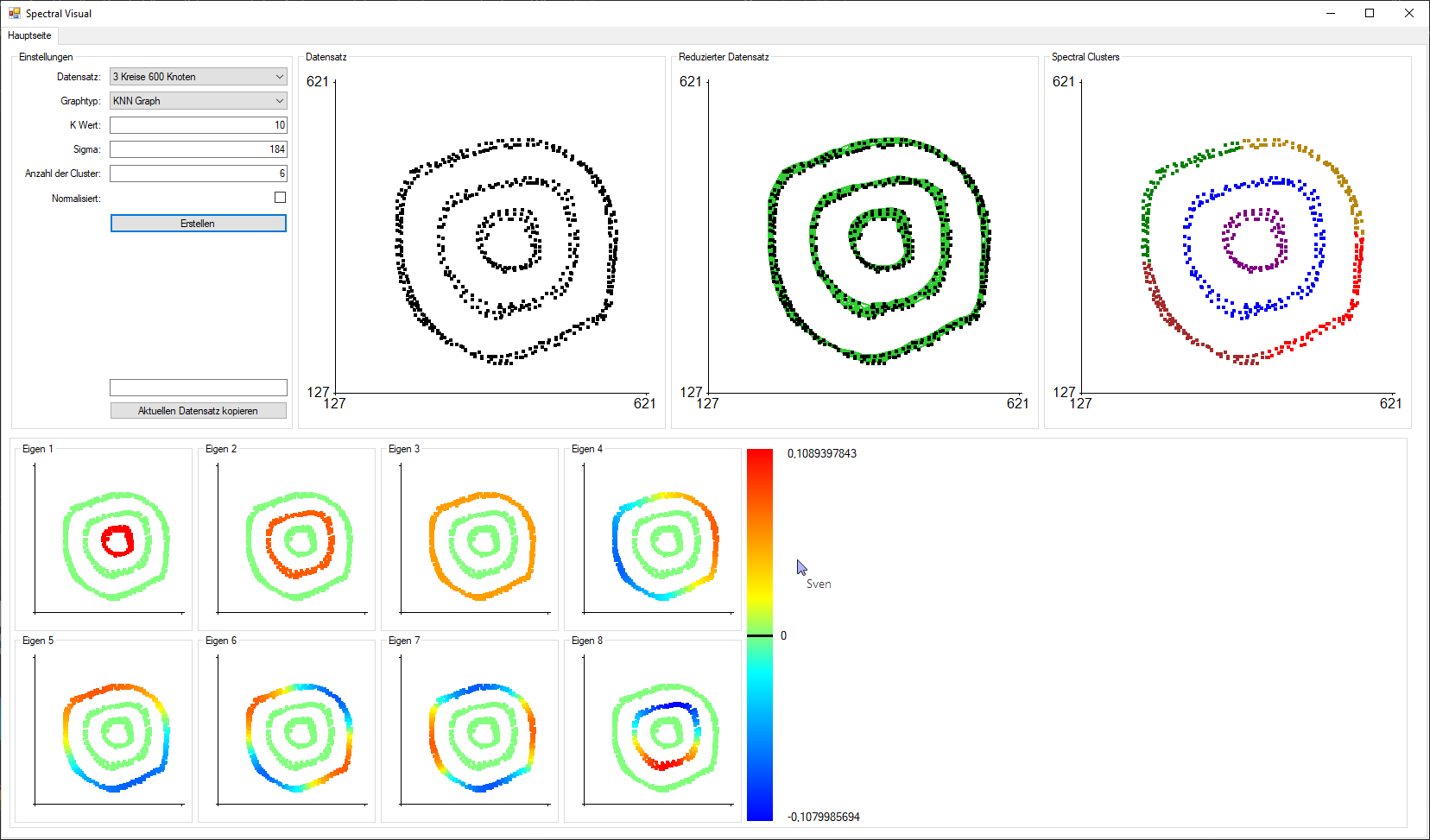 Abbildung 6: Spectral Visual(Graphtyp: KNN, K Wert: 10, Sigma: 184, Clusteranzahl: 6)
Abbildung 6: Spectral Visual(Graphtyp: KNN, K Wert: 10, Sigma: 184, Clusteranzahl: 6)
Bewertung
Spectral Clustering ist ein sehr flexibler Algorithmus für das Bilden von Cluster.
Es benötigt einiges an Erfahrung, um Spectral Clustering voll auszureitzen, dafür liefert es dann sehr genaue und konstante Lösungen.
Verwendet man Spectral Clustering in einem Bereich mit Graphen, die ähnliche Eigenschaften, wie Dichte, aufweisen, z.B. Soziale Netzwerke, so
entfällt größenteils das Problem mit den zu wählenden Parametern, weshalb sich hier Spectral Clustering sehr gut eigenet.
5. Zusammenfassung und Ausblick
Spectral Clustering ist eine komplexe aber richtig angewendet zuverlässige Art um Gruppen aus verstrickten Datenmengen zu bilden. Dank seiner Komplexität lässt sich diese Clustermethode vielseitig einsetzen,
muss jedoch richtig bedient werden.
Wir sehen großes Potential im Bereich des Spectral Clustering, bei all den Details, zu denen es keine genauen Aussagen zu geben scheint.
6. Referenzen
- Donath, W. E., & Hoffman, A. J. (2003). Lower bounds for the partitioning of graphs. In Selected Papers Of Alan J Hoffman: With Commentary (pp. 437–442). World Scientific.
- Fiedler, M. (1973). Algebraic connectivity of graphs. Czechoslovak Mathematical Journal, 23(2), 298–305.
- Shi, J., & Malik, J. (2000). Normalized cuts and image segmentation. IEEE Transactions on Pattern Analysis and Machine Intelligence, 22(8), 888–905.
- Meila, M., & Shi, J. (2001). A Random Walks View of Spectral Segmentation.
- Ng, A. Y., Jordan, M. I., & Weiss, Y. (2002). On spectral clustering: Analysis and an algorithm. Advances in Neural Information Processing Systems, 849–856.
- Von Luxburg, U. (2007). A tutorial on spectral clustering. Statistics and Computing, 17(4), 395–416.
- Von Luxburg, U., Belkin, M., & Bousquet, O. (2008). Consistency of spectral clustering. The Annals of Statistics, 555–586.