Beispiele von Multilayer-Netzwerken
| Elizabeth Kublanov | Henri Nagel | Lars Dirschauer | ||
|---|---|---|---|---|
| RWTH Aachen University | RWTH Aachen University | RWTH Aachen University | ||
| elizabeth.kublanov1@rwth-aachen.de | henri.nagel@rwth-aachen.de | lars.dirschauer@rwth-aachen.de |
1. Abstract
Multilayernetzwerke können in vielen verschiedenen Bereichen, wie beispielsweise in den menschlichen oder auch tierischen Interaktionen, in biologischen Thematiken, wie dem Innenleben des menschlichen Genoms, die dort vorherrschenden Beziehungen, in Form eines Graphen darstellen. Mithilfe der Darstellung in Form von Multilayernetzwerken Erkenntnisse gezogen und Vorhersagen getroffen werden.
Aufgrund der Vielfältigkeit von Multilayernetzwerken und deren Anwendungen in den unterschiedlichsten Bereichen, kann es schnell unübersichtlich werden. Da das Thema zudem relativ jung ist, können nicht viele geeignete Ansätze für eine Klassifizierung dieser verschiedenen Möglichkeiten gefunden werden. Um einen generellen Überblick über die Vielfältigkeit von Multilayernetzwerken und deren Anwendungsbereichen zu verschaffen, werden im Laufe der folgenden Arbeit verschiedene Beispiele von Multilayernetzwerken aufgegriffen und anhand von bestimmten Charakteristika voneinander abgegrenzt. Zudem werden Vor- und Nachteile dieser Darstellung erläutert und deren Anwendungsbereiche erörtert.
___
Inhaltsverzeichnis
1. Einleitung
Es ist üblich, die Beziehungen zwischen Einheiten in realen Systemen anhand eines einfachen Graphen zu modellieren. Die Realität wird jedoch besser durch mehrere voneinander abhängige Teilsysteme (oder Schichten) dargestellt. Motiviert durch dieses Problem wurde kürzlich das Konzept eines mehrschichtigen Netzwerkmodells (Multilyernetzwerk) im Bereich der Graphentheorie entwickelt. Hierbei werden Knoten auf mehrere Ebenen aufgeteilt und mit inter- sowie intraschichtlichen Kanten verbunden. Die Art nach denen man diese Netzwerke konfiguriert, also wie man Knoten und Kanten auf Schichten aufteilt, ist sehr vielfältig. Knoten können nur zu bestimmten Schichten gehören oder jede Schicht beinhaltet alle Knoten. Es können inter-schichtliche Kanten geben oder nicht. Sichten können beliebig aufgeteilt werden, zum Beispiel kann man Knoten oder Kanten nach bestimmte Eigenschaften kategorisieren und nach diesen auf Schichten aufteilen. Zudem können auch Abhängigkeiten zwischen Knoten im Kontext des zu modellierenden Systems dargestellt werden oder nur deren Verbundenheit. Aufgrund dieser Vielfältigkeit und der laufenden, schnellen Erforschung solcher komplexen Netzwerke fehlen standardisierter Namenskonventionen, da verschiedene Gruppen überschneidende und widersprüchliche Terminologie verwenden, um bestimmte Netzkonfigurationen zu beschreiben. Dies erschwert die Forschung auf diesem Gebiet, weshalb wir in dieser Arbeit schon eingeführte Konventionen für verschiedene Multilayernetzwerk Implementaionen zusammenfassen und diese anhand von entsprechenden Beispielen präsentieren. Hierdurch soll die Charakteristik und der Anwendungsbereich der verschiedenen Arten hervorgeholt werden, was ein reibungsloseres Finden verwandter Arbeiten ermöglicht und folglich einen größereren Grundstein im Bereich der Forschung mit und um Multilayernetzwerken aufbaut.
2. Verwandte Arbeiten
Multilayernetzwerke spielen seit den letzten Jahren eine große Rolle in der Forschung um und mithilfe der Grafentheorie. Aus dieser Bewegung heraus haben viele Arbeiten versucht eine Einführung in das Konzept der Multilayernetzwerke zu geben und diese formal zu definieren, um einen Grundstein für weitere Forschung zu legen (Kivela et al., 2014), (Marcello Tomasini, 2015), (Porter, 2018). Dieser Grundstein ist jedoch sehr vage, da das Thema noch sehr jung ist und sich noch nicht viele Konventionen konstruktiv durchgesetzt haben. Terminologien sind meist verschieden, obwohl gleiche Prinzipien angewandt werden oder es gibt sehr schwimmende Grenzen zwischen verschiedenen Arten von Multilayernetzwerken (Hammoud & Kramer, 2020). Motiviert durch dieses Problem haben Hammoud, Z. und Kramer F. (Hammoud & Kramer, 2020) versucht Konventionen zusammenzufassen und diese festzuhalten. Hierbei wurde vor allem der Fokus darauf gelegt verschiedene Arten von Multilayernetzwerken zu kategorisieren und klare Grenzen zwischen diesen zu ziehen, auf welche wir in unserer Arbeit primär beziehen werden. Hammoud, Z. und Kramer F. haben hierbei Arten von Multilayernetzwerken in fünf verschiedenen Implementationen klassifiziert, welche sich auf zwei Hauptaspekte einteilen lassen (siehe Tabelle 1).
| Aspekt | Implementation | Anwendungsbeispiel |
|---|---|---|
| Edge-colored | Multiplex | (Cardillo et al., 2013) |
| Multilevel | (Zhao & Lei, 2019) (Odri et al., 1993) | |
| Node-colored | Interconnected | (Hammoud & Kramer, 2020) |
| Interdependent | (Kong et al., 2019) | |
| Multitype | (Allard et al., 2009) | |
| Hypernetzwerke | (Hammoud & Kramer, 2020) |
Tabelle 1: Klassifikation verschiedener Multilayernetzwerk Implementationen aufgeteilt auf zwei Aspekte (Hammoud & Kramer, 2020)
Andere Arbeiten verwenden Multilayernetzwerke verschiedener Natur um neue Forschungsergebnisse zu erzielen (Cardillo et al., 2013). Hierbei finden Multilayernetzwerke Anwendung in einem breiten Spektrum von Bereichen: Biologie (Hammoud & Kramer, 2020), Neurologie (Odri et al., 1993), Datenwissenschaften (Kong et al., 2019) und vielen weiteren. Diese Arbeiten und andere beschäftigen sich weiterführend damit, warum sie besonders in diversen Anwendungsbereichen geeignet sind, welche Herausforderungen sie mit sich bringen und wie man mit ihnen möglichst präzise Ergebnisse erzielen kann (Cardillo et al., 2013). Aus diesem Becken der Anwendungen von Multilayernetzwerken werden wir für die verschiedenen Implementationen Beispiele schöpfen und anhand dieser die Anwendungsbereiche, Charakteristik sowie Vor- und Nachteile dieser darstellen.
3. Methodik
3.1 Edge-Colored (Kanten gefärbte) Graphen
Im folgenden Abschnitt werden verschiedene Arten von Multilayernetzwerken behandelt, die sich auf edge-colored Graphen zurückführen lassen. Edge-colored Graphen stellen Systeme mit heterogenen Verbindungen dar (Hammoud & Kramer, 2020). Hiermit ist gemeint, dass es im Graphen mehrere Arten von Knotenpunkten gibt, zwischen denen unterschieden werden kann. Im Folgenden werden diese Graphen einmal formal definiert, hierbei stützen wir uns auf die Arbeiten von (Hammoud & Kramer, 2020) und (Wang & Li, 2009):
Sei \(G = (V,E,C: E \rightarrow N)\) ein edge-colored Graph, wobei \(N\) eine Teilmenge der natürlichen Zahlen darstellt (Hammoud & Kramer, 2020),(Wang & Li, 2009). Die Abbildung \(C\) dient zur Kantenfärbung. Sie bildet jede Kante auf ein Element \(c \in N\) ab. Jedes \(c\) kategorisieren die Kanten und können Grafisch Beispielhaft durch Farben dargestellt werden (Hammoud & Kramer, 2020),(Wang & Li, 2009). Lässt sich \(G\) eine solche Abbildung \(C\) zuordnen, nennt man \(G\) einen edge-colored (kanten gefärbten) Graphen (Wang & Li, 2009). Ein Teilgraph \(M_c = (V, \{\forall e \in E : C(e) = c, c \in N\})\) von \(G\) beschreibt somit den Teilgrafen mit allen Kanten der Farbe \(c\). Diese Art edge-colored Graphen aufzuteilen wird im Verlauf dieses Abschnittes an Bedeutung gewinnen.
3.1.1 Multiplexe Multilayernetzwerke
Multiplexe Netzwerke sind edge-colored Graphen, wobei jede Schicht des Netzwerkes alle Knote beinhaltet. Die Kanten sind hierbei je nach ihrem Typ den verschiedenen Schichten zugeordnet. Hierdurch visualisieren Multiplex-Netzwerke die Interkonnektivität desselben Systems in mehreren Kanälen, die durch die Schichten dargestellt werden. (Hammoud & Kramer, 2020)
Ein Anwendungsbeispiel für ein solches Netzwerk ist die graphische Repräsentation des europäischen ATN (“Aeronautical telecommunication network” zu Deutsch: Luftfahrt-Telekommunikations Netzwerk). In der Arbeit von Cardillo, A. et al. (Cardillo et al., 2013) stellen 37 Schichten verschiedene kommerzielle europäische Flugunternehmen dar, wobei die Knoten jeder Schicht alle europäischen Flughäfen zeigen. Hierbei bleiben die Knoten auf jeder Ebene gleich, auch wenn sie vom Grad 0 sind, also keine Kanten von ihnen aus gehen. Dies hebt die multiplexe Charakteristik des Netzwerkes hervor. In der Arbeit von Cardillo, A. et al., aus der wir dieses Beispiel beziehen, wurde der Fokus auf das schrittweise zusammenführen von Schichten und wie sich verschiedene strukturelle Maßen durch dieses Prozedere entwickeln gelegt (Cardillo et al., 2013). Dies zeigt eine Möglichkeit, wie mit Multiplexen Multilayer Netzwerken analytisch umgegangen werden kann, weitreichend wird sich diese Arbeit jedoch nicht mit dieser Methodik beschäftigen, da dies den Rahmen überschreiten würde.
Jedoch werden wir, um genauer auf das Beispiel einzugehen nun eine auf zwei Schichten reduzierte Repräsentation des europäischen ATN betrachten (Fig. 3.1.1). Die Schichten stellen hierbei jeweils eine Teilmenge der verschiedenen Flugunternehmen dar: einmal die Zusammenführung von größeren Fluggesellschaften (c) und von kostengünstigen (d).
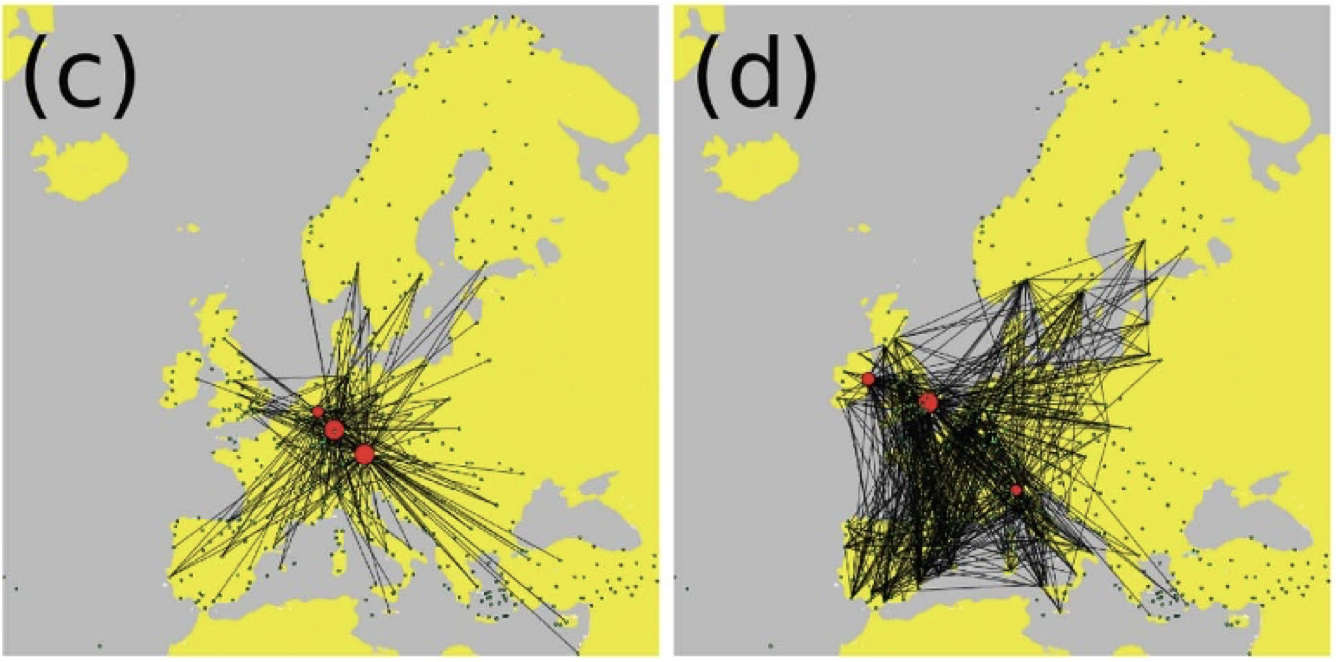
Beispiel 2: multiplexes Multilayernetzwerk zur Modellierung des ATN (Cardillo et al., 2013)
In der Studie von Cardillo, A. et al. (Cardillo et al., 2013) wurde durch den Vergleich dieser beiden Schichten gezeigt, dass die topologischen Eigenschaften des ATN sich nicht in einzelnen Schicht auftreten, sondern mit der Multilayer Charakteristik des Systems zusammenhängen. Akzentuiert wird durch diese Erkenntnis, dass es wichtig ist, den Multiplex-Charakter der meisten realen vernetzten Systeme zu berücksichtigen, um präzisere Ergebnisse erzielen zu können. Auch folgt aus der Arbeit, dass das verschiedene Verschmelzen von mehren Schichten in qualitativen Differenzen in den Gesamtnetzen resultiert (Cardillo et al., 2013). Dies zeigt die Bedeutsamkeit der Betrachtung von Schichten eines Netzwerkes als relevante Einheit für dieses. Dies kann zu einem besseren Verständnis und einer besseren Modellierung von dynamischen Prozessen auf der Ebene des Gesamtnetzes beitragen.
Aus dem präsentierten Beispiel lässt sich die Charakteristik und der Anwendungsbereich von Multiplex Netzwerken gut zeigen. Sie lassen sich direkt aus einem edge-colored Graphen übersetzen, ohne dass dabei weitere Daten benötigt werden (z.B. Kanten zwischen den Schichten). Auch kann man Schichten frei wählen und nach Belieben komprimieren, diese ist zwar nicht verlustfrei doch vereinfacht die Komplexität der Analyse. Durch diese beiden Punkte zeigt sich, dass Multiplex Netzwerke sehr flexibel und einfach (ohne das Benötigen von weiteren Daten) anwendbar sind, um präzisere und den zu modellierenden Prozessen näheren Ergebnisse zu erzielen.
3.1.2 Multilevel Multilayernetzwerke
Ein Multilevel Network besteht, wie der Name schon hergibt, aus mehreren Levels.
Das im Folgenden aufgegriffene Beispiel basiert auf der Arbeit von Jie Zhao und Xiujuan Lei (Zhao & Lei, 2019) .
Proteine sind Teile eines Proteinkomplexes, also einer Zusammenlagerung mehrerer Proteine.Jedes dieser Proteine besitzt bestimmte Funktionen, welche in der GO-Annotation (Gene Ontology) festgehalten wird.
Um diese Strukturen nun in einem Multilayer Netzwerk festzuhalten,welches in diesem Falle zusätzlich noch ein overlapping Multilayer Network ist, wird zunächst ein gewichtetes PPI Netzwerk(Protein-Pprotein Interactions Network) erstellt. Besitzen nun 2 Proteine mehrere gemeinsame GO-Annotationen, wird die Wertigkeit der Verbindung mithilfe der Formel:
\[W_{v_i,w_j}=\frac{|GO_{v_i}\cap GO_{v_j}|}{min(|GO_{v_i}|,|GO_{v_j}|)}\]Berechnet.
Die obere Berechnung gleicht der Anzahl derjenigen GO-Annotationen, die gleich sind.Diese wird daraufhin durch die minimale Anzahl der GO-Annotationen also der kleineren Gesamtanzahl der Funktionen der zwei Proteine geteilt. Überschreitet das Ergebnis einen Wert von \(0.6\), wird die Verbindung zwischen diesen beiden Proteinen im PPI-Network festgehalteAndernfalls wird es aus dem PPI-Network gelöscht.
Das erstellte PPI-Netzwerk ist in Form eines Graphen \(G(V, E)\) dargestellt,in dem V für die Proteine und E für deren Verbindungen steht.
In dem Multilayer-Netzwerk stellt dieser Graph G den obersten Layer dar. Um die darauffolgenden Layer zu kreieren, erfolgen 2 zusammenhängende Schritte. Im ersten Schritt wird ein Maximum Complete Subgraph erstellt.In diesem Verfahren wird ein Knoten \(v_i\) und die Verbindung dessen zu seinen Nachbarn betrachtet.So versucht man einen größtmöglich zusammenhängenden Graphen zu erstellen,in welchem jeder Knoten eine Verbindung zu jedem der Nachbarknoten und dem Knoten \(v_i\) besitzt. Dies wird für jeden einzelnen Knoten \(v_i\) gemacht, sodass mehrere Maximum Complete Subgraphs entstehen.
Im nächsten Schritt werden nun die einzelnen Subgraphs als Knoten dargestellt.Dabei besteht zwischen zwei Knoten genau dann eine Verbindung,wenn innerhalb der zwei Subgraphs eine Überschneidung der Proteine stattfand.
Der so entstandene Graph G1 stellt in dem Multilayer-Netzwerk den zweiten Layer dar. Das zuvor beschriebene Verfahren wird so lange angewendet, bis keine Bildung eines Maximum Complete Subgraphs mehr möglich ist.
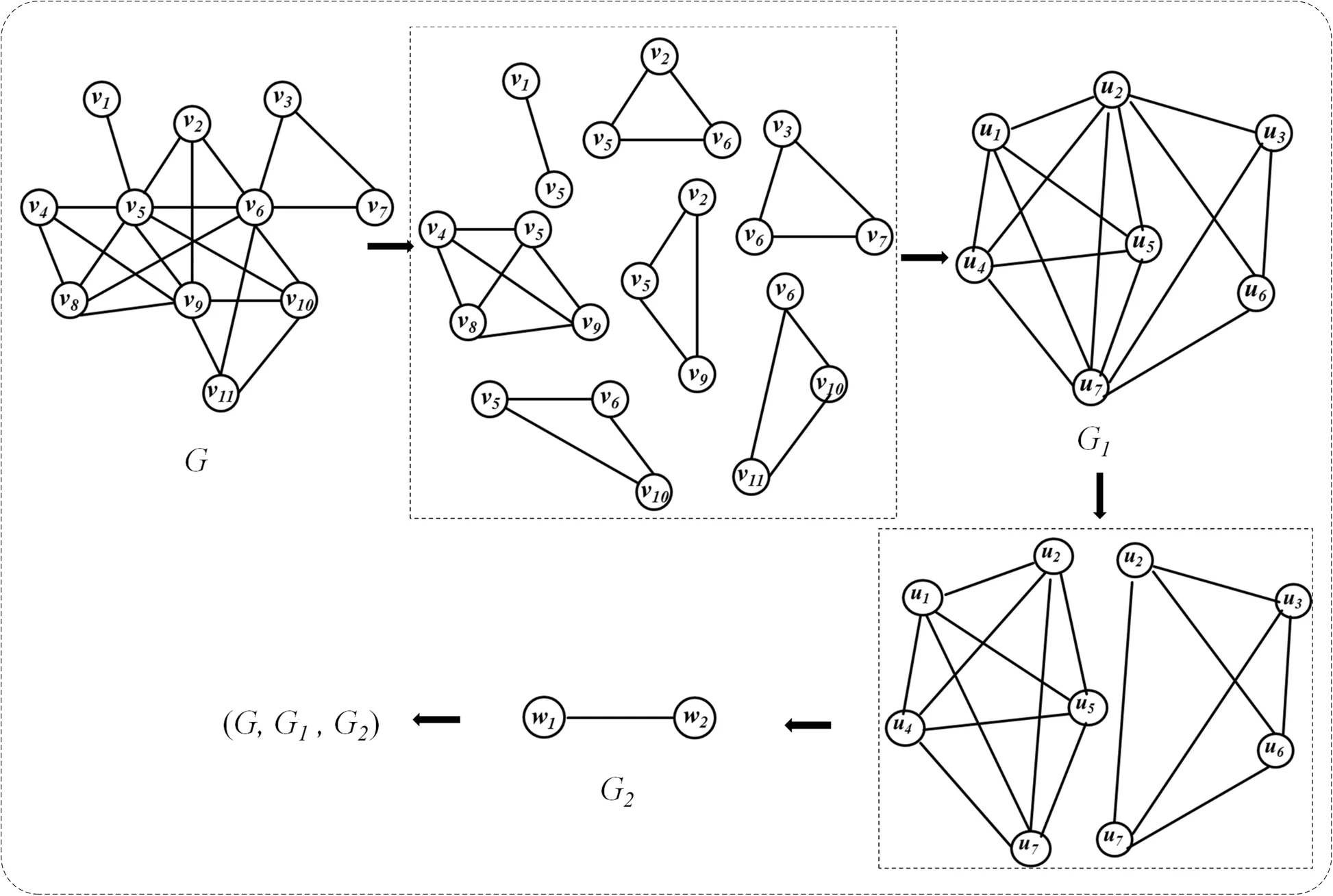
Multilayer Netzwerk: Beispiel 1; (Zhao & Lei, 2019)
Als weiteres Beispiel für ein Multilayer-Netzwerk kann das Multilayer Neural Network aus dem Artikel ”Multilayer motif analysis of brain networks” (Odri et al., 1993), dienen. Dieses befasst sich im Groben mit der Darstellung und Analyse der neuronalen Gegebenheiten, beim Erlernen neuer Fähigkeiten. Auch hier ist das Netzwerk ein Graph \(G(V, E)\), in dem V die Neuronen und E die Verknüpfungen zwischen diesen demonstriert. Den ersten Layer stellt der Input Layer dar. Durch diesen Layer werden Daten gewichtet in das Netzwerk eingefügt, welche im Fortschreiten durch die darauffolgenden Layer weiter verarbeitet werden. Der Hidden Layer repräsentiert das Vorgehen eines biologischen Neurons. Diese Neuronen sind mit einem bestimmten vorgegebenen Wert (Bias) assoziiert. Für jedes eintreffende Signal wird ein a mithilfe der Formel \(a=(\text{Eingabe} \cdot \text{Gewichtung})\). Sei nun \(a_i\) ein Signal, dass in Neuron B ankommt und \(\sum_{i=0}^{k} a_i\) die Summe alles Signale, die in einem Neuron B ankommen. So kann die activationfunction mithilfe der Formel: \(\sum_{i=0}^{k} a_i + (\text{Gewichtung})\) berechnet werden, welche angibt, ob ein Neuron aktiv ist, oder nicht. Im Falle einer Aktivierung leitet dieses die Signale zu den Neuronen des darauffolgenden Layers weiter. Im Output Layer erfolgt eine Vorhersage, welche Neuronen aktiv und welche inaktiv waren.
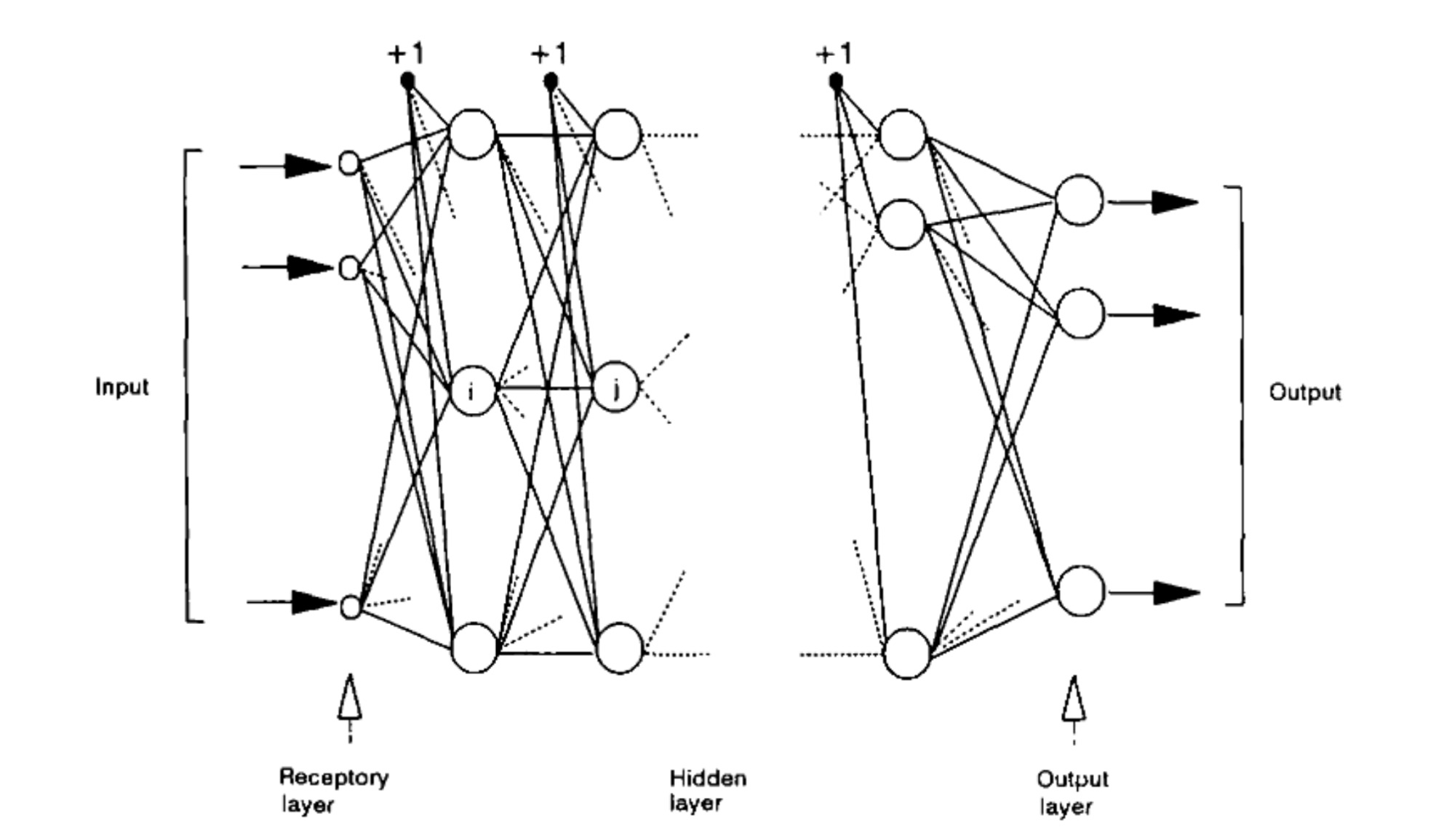
Multilayer Netzwerk: Beispiel 2; (Odri et al., 1993)
3.2 Node-Colored (Knoten gefärbte) Graphen
Node-colored Graphen beschreiben Graphen mit heterogenen Knoten. Multilayernetzwerke die aus diesen Grapen erzeugt werden können werden im folgenden Abschnitt behandelt, weshalb wir hier diese Art der Graphen einmal formal definieren.
Analog zu edge-colored Graphen wird ein node-colored Graph \(G\) durch ein Triplet definiert mit \(G = (V, E, C)\). \(V\) stellt hierbei die Menge der Knoten und \(E\) die Menge der Kanten dar. Die Abbildung \(C : V \rightarrow N\) bildet die Knoten auf einen Menge aus natürlichen Zahlen ab. Die Elemente \(c\) aus \(N\) stellen hierbei wieder kategoriene dar, nachdenen jedoch die Knoten und nicht Kanten eingeordnet werden. Diese können wieder durch Farben graphisch dargestellt werden.
3.2.1 Interdependente Multilayernetzwerke
Für die Konvention der Interdependenten Multilayernetzwerken lässt sich schwer ein klarer Konsens finden. In dieser Arbeit beziehen wir uns auf die Rahmenvereinbarungen von Hammoud, Z. et al. (Hammoud & Kramer, 2020) und Castet et al. (Castet & Saleh, 2013). Interdependenten Multilayernetzwerken beschreibt hier das in Abhängigkeit setzten von mehreren monoplexen Netzwerken (Hammoud & Kramer, 2020),(Castet & Saleh, 2013). Abhängigkeit bzw. Interdependenz beschreibt im Kontext der Graphen eine bidirektionale Interaktion zwischen zwei Knoten (Kong et al., 2019). Bei interdependenten Multilayernetzwerken werden die monoplexen Netzwerke durch die verschiedenen Schichten repräsentiert, wobei Kanten zwischen diesen die einzelnen Netzwerke verbinden. Dadurch zeigt sich, dass es sich um ein Knoten gefärbtes Netzwerk handelt, denn Konten jeder Schicht können, projiziert auf ein monoplexes Netzwerk, heterogen durch ein Schlüsselmerkmal (zum Beispiel Zugehörigkeit eines Subsystems) unterschieden werden. Die Menge der Knoten verschiedener Schichten müssen keine Schnittmenge haben, können also komplett disjunkt sein.
Zur Visualisierung dieser Art von Multilayernetzwerken haben wir ein Beispiel aus einer Arbeit von Kong, J. et al. (Kong et al., 2019) gewählt (siehe Fig. 3.2.1). In dieser wurde beispielhaft eine soziale Infrastruktur modelliert. Subsysteme dieser sind jeweils auf die Schichten aufgeteilt. Kanten zwischen den Schichten stellen hierbei eine Abhängigkeit von zwei Knoten aus verschiedenen Systemen dar. Wichtig zu beachten hierbei ist, dass Knoten abhängig von Knoten aus beliebigen Schichten sein können.
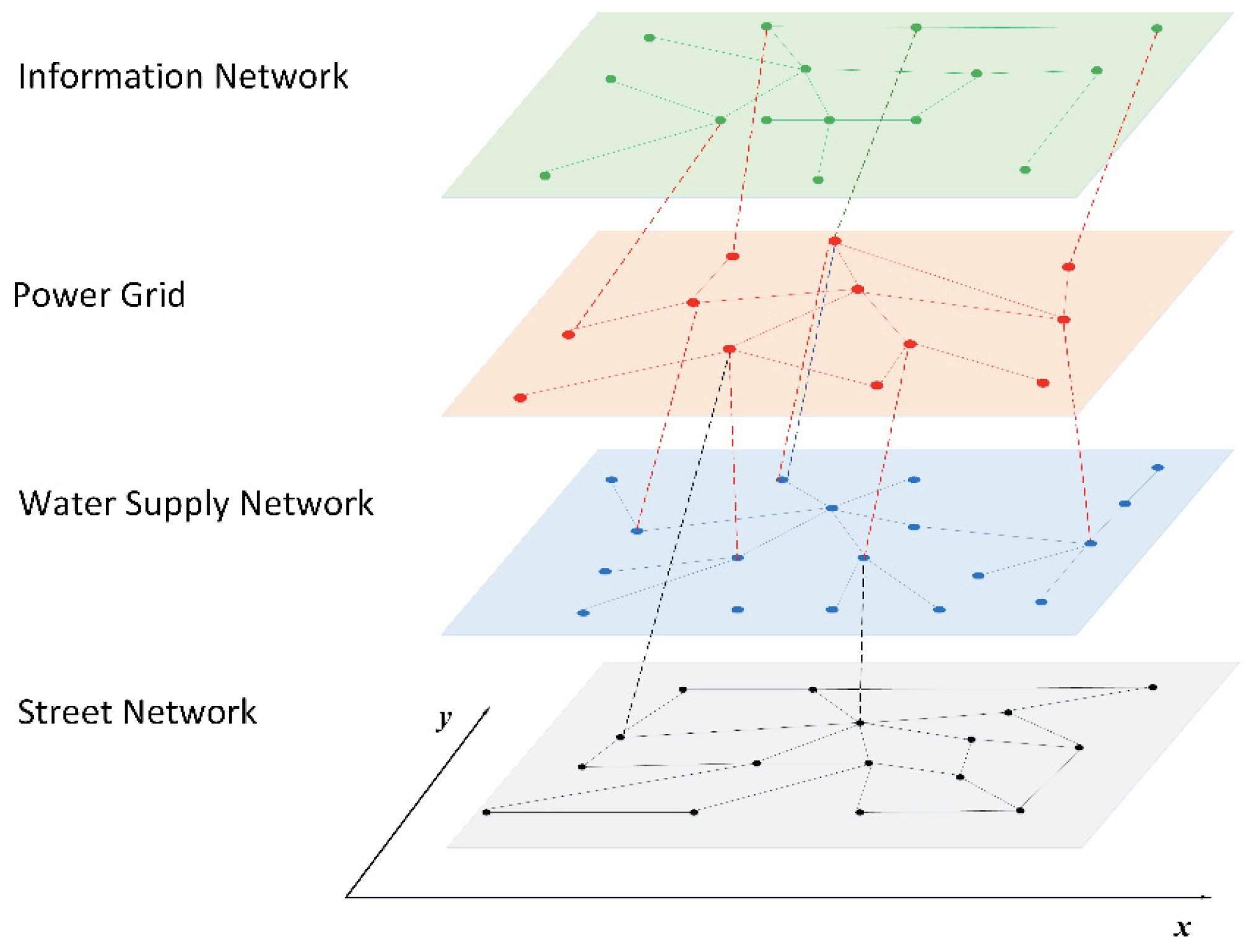
Fig. 3.2.1: interdependentes Multilayernetzwerk zur Modellierung einer (sozialen) Infrastruktur (Kong et al., 2019)
Wie man an dem Beispiel sehen kann, eigenen sich interdependente Multilayernetzwerke besonders gut, um die Abhängigkeit zwischen verschiedenen Subsystemen eines komplexen Systems zu visualisieren, ohne diese dabei zu abstrahieren (Kong et al., 2019),(Hammoud & Kramer, 2020). Durch diese Abhängigkeit zwischen verschiedenen Schichten haben diese Art von Netzwerke eine starke Kaskadenfehleranfälligkeit (Hammoud & Kramer, 2020). Kaskadenfehler beschreiben, wie der Ausfall eines Knotens oder eines kleinen Teils von Knoten in einem Netz den Ausfall anderer Knoten im Netz verursacht (Wang et al., 2014). Damit wie man interdependente (multilayer) Netzwerke robuster gestalten kann ist ein laufendes Thema in der Netzwerktheorie (Hammoud & Kramer, 2020),(Wang et al., 2014),(Kong et al., 2019).
3.2.2 Interconnectedte Multilayernetzwerke
Das folgende Beispiel eines Interconnected Networks besteht aus mehreren Monoplex-Netzwerken, welche miteinander agieren. Die Knoten dieser Netzwerke können sowohl Intrakanten als auch Zwischenkanten besitzen, welche die Knoten verbinden.(Hammoud & Kramer, 2020) Interconnected Networks können sowohl in Monoplex-Ansicht als auch in Multilayer-Ansicht dargestellt werden. Die Zwischenkanten \(E\) definieren die Wechselwirkungen zwischen den \(L\) verschiedenen Monoplex-Netzwerken, welche von voneinander abhängigen Netzwerken abhängig sind. Das mehrschichtige Modell, welches aus den einzelnen Netzwerken besteht, ist sowohl knotenfarben als auch schichtdisjunkt und wird gebildet durch das einbetten der verschiedenen Monoplex-Netzwerke in jeweils eine einzelne Schicht und dem anschließenden Verbinden mit ihren Zwischenkanten. Diese Netzwerke tragen dazu bei, eine globale Synchronisation zwischen verschiedenen Subsystemen zu erreichen.(Hammoud & Kramer, 2020)
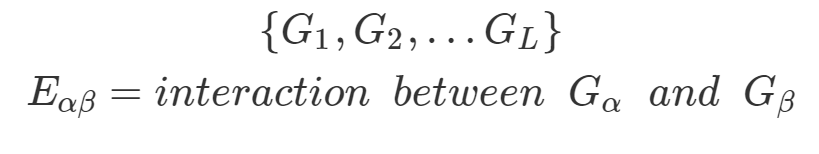
Gleichung 2: Interconnected Network (Hammoud & Kramer, 2020)
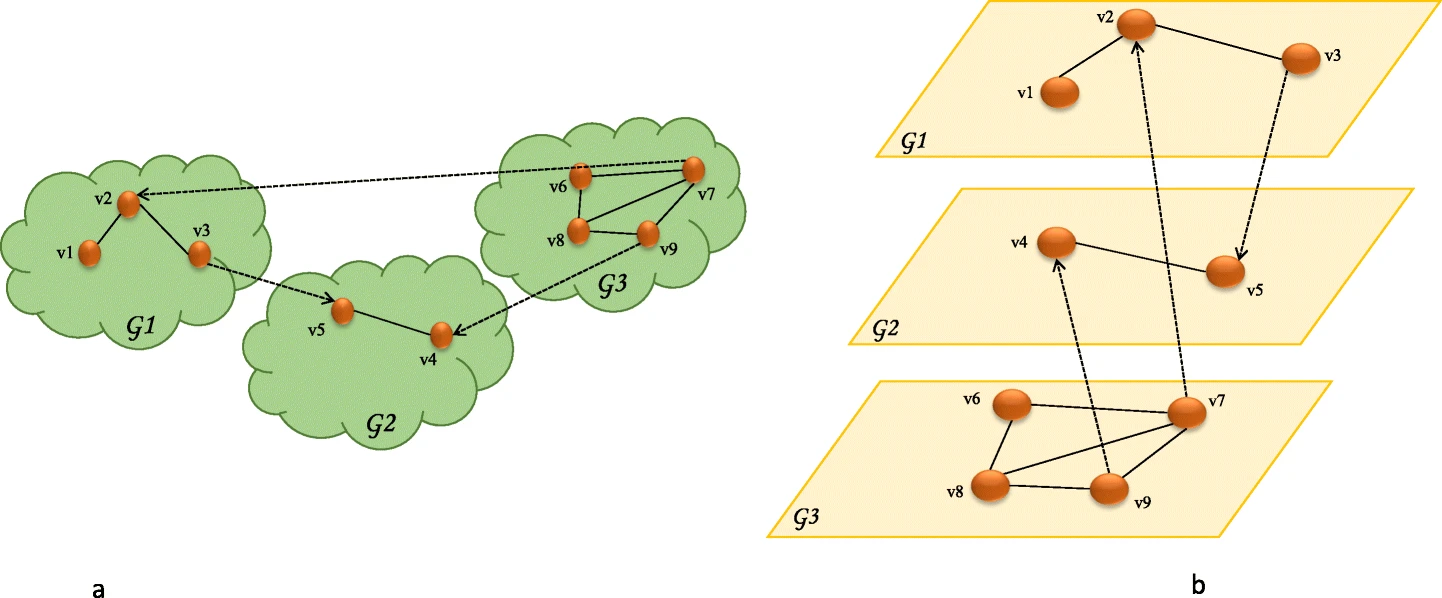Abbildung: Interconnected Network (Hammoud & Kramer, 2020)
Solche Netzwerke werden unter anderem für Transportnetze, für die Telekommunikation, für Stromnetze und auch für soziale Netzwerke verwendet. Gerade ein Infrastrukturnetz ist ein im Normalfall ein gutes Beispiel für ein Interconnected Network, denn dieses benötigt Strom um zu funktionieren, d. h. alle einzelne Netzwerke sind vom Strom abhängig, ein Ausfall kann das gesamte Netzwerk beeinträchtigen.(Hammoud & Kramer, 2020) Ein ähnliches Beispiel ist der folgende Graph. Hier sind mehrere local und main switches in einem local Area Network abhängig von dem Central switch, fällt dieser aus, kann man nicht mehr über die switches auf den Router zugreifen und das local Area Network wird lahmgelegt, folglich kann man nicht mehr in das Internet gehen oder im LAN über den Central Switch Daten austauschen.[Fig.3]
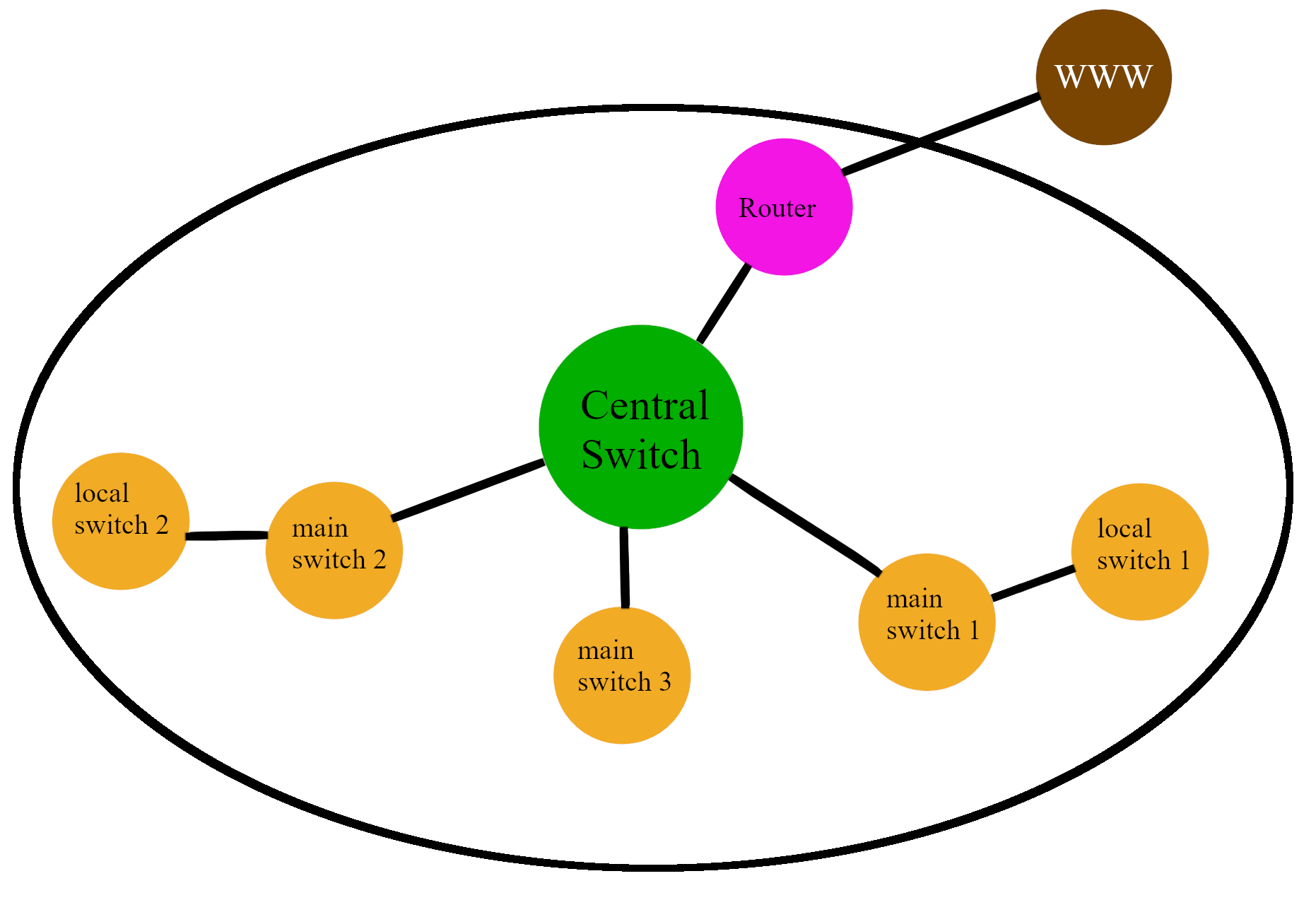
Abbildung: Local Area Network, an Interconnected Network; eigene Graphik
3.2.3 Multitype Multilayernetzwerke
Ein Multitype Network ist ein Colored-Node Network, in welchem die unterschiedlichen Typen der Knoten hervorgehoben werden.
Das folgende Beispiel wird sich auf die in der Arbeit von Funk, Sebastian und Jansen, Vincent A. A. (Allard et al., 2009) thematisierte Darstellung von Multitype Netzwerken beziehen.
So gibt es in einem solchen, wie auch in Fig. 1 repräsentiert, \(N\) Nodes, \(M\) Typen und Type-\(i\) Nodes, welche ein Teil \(w(i)\) des Netzwerks besetzen.
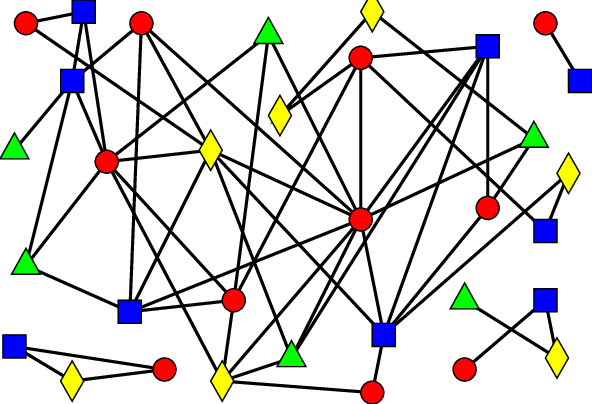
Schematic representation of an undi-rected multitype network with M= 4, N= 33, w1=311 ,w2=13,w3=211 and w4=733 where types 1,2,3 and 4 re-fer to squares, circles, triangles and diamonds respectively.Edges running between nodes are bidirectional and can thusbe followed in either directions. (Allard et al., 2009)
Bestehende Verbindungen der Type-i Nodes werden durch die Funktion \(P_i(k_1,k_2,\dots,k_n)=P_i(k)\) angegeben, welche die Wahrscheinlichkeit einer Verbindung eines belibig gewählten Type-i Knotens und einem \(K_1\) Type-1, Knoten, einem \(K_2\) Type-2 Knoten, etc. angibt. Des Weiteren wird ein \(z_{ij}\) als Kante von Type \(i\) zu Type \(j\) definiert und lässt sich mithilfe von \(P_i(k)\) berechnen, durch die Funktion:
\[z_{ij}=\sum_{k_1=0}^{\infty}\dots \sum_{k_M=0}^{\infty} k_j P_i (k_1,\dots,k_M) \equiv \sum_{k=0}^{\infty} k_j P_i(k)\]$$w=\begin{bmatrix} w_{1} & 0 & \dots & 0 \\ 0 & w_2 & \dots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \dots & w_M \end{bmatrix}$$ $$z=\begin{bmatrix} z_{11} & z_{12} & \dots & z_{1M} \\ z_{21} & z_{22} & \dots & z_{2M} \\ \vdots & \vdots & \ddots & \vdots \\ z_{M1} & z_{M2} & \dots & z_{MM} \end{bmatrix}$$
Bond occupation probability matrix:
\[T=\begin{bmatrix} T_{11} & T_{12} & \dots & T_{1M} \\ T_{21} & T_{22} & \dots & T_{2M} \\ \vdots & \vdots & \ddots & \vdots \\ T_{M1} & T_{M2} & \dots & T_{MM} \end{bmatrix}\]In dieser Matrix stellt \(T_{ij}\) die Wahrscheinlichkeit der Besetzung der Kante \(i \rightarrow j\) dar.
Die Nutzung von Multitype Netzwerken ermöglicht eine Vermischung von Knoten, wie beispielsweise das Clustering, oder Assortative mixing, bei welchem Knoten eine Verbindung mit denjenigen Knoten eingehen, die ähnliche Eigenschaften besitzen.
Durch die bond occupation probability können Korrelationen zwischen den Besetzungswahrscheinlichkeiten der Kanten und den durch sie verbundenen Knoten, erzeugt werden.
3.2.4 Multi-Hypernetworks
Hypernetzwerke sind Multilayernetzwerke, welche von verschiedenen sich überschneidenden Gemeinschaften oder Teilnetzwerken gebildet werden. Im Gegensatz zu normalen Netzwerken, besitzen Kanten in Hypernetzwerken sog. Hyperkanten, diese können mehrere Knoten gleichzeitig verbinden. Hierbei liegt der Fokus bei den Knoten, welche untereinander verbunden sind. Knoten in derselben Teilmenge werden einer Schicht mit vollständig verbundenen Knoten zugeordnet. Ein Multi-Hypergraph (Gleichung 1) wird durch ein Paar \((X, H)\) definiert, wobei \(X\) die Menge von Knoten ist und H eine Multimenge von Teilmengen von \(X\), die die Kanten sind.(Hammoud & Kramer, 2020)
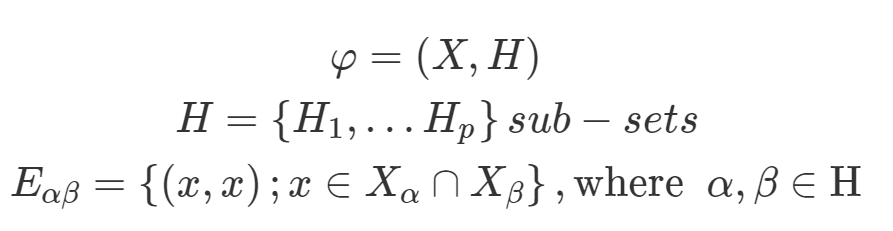
Gleichung 1: Multi-Hypergraph (Hammoud & Kramer, 2020)
Hypernetzwerke sind optimale Darstellungen von Netzwerken mit n-stelligen Beziehungen, da sie Hyperkanten ermöglichen, die mehr als 2 Knoten gleichzeitig verbinden.(Hammoud & Kramer, 2020)
Ein einfaches Beispiel für diese Art von Netzwerk ist ein Netzwerk, welches den Fokus auf die Familie und das Arbeitsleben legt. Hier hat eine Person (Knoten 1) eine Verbindung mit allen Familienmitgliedern, welche sich alle untereinander kennen, und eine Verbindung mit allen Arbeitskollegen, welche sich alle untereinander kennen. Die gesamte Familie bildet die erste Schicht, da alle Knoten (Personen) aufgrund der Bekanntschaft miteinander verknüpft sind. Die zweite Schicht sind die Arbeitskollegen, welche ebenfalls alle miteinander verknüpft sind. Die Familienmitglieder und die Arbeitskollegen kennen sich nicht, daher sind zwischen diesen keine Kanten vorhanden. Der Knoten 1 ist der einzige Knoten, der in beiden Ebenen existiert, da er mit allen Personen eine Beziehung hat. Knoten welche dieser Eigenschaft entsprechen, werden schichtübergreifend miteinander verbunden.(Fig.1)
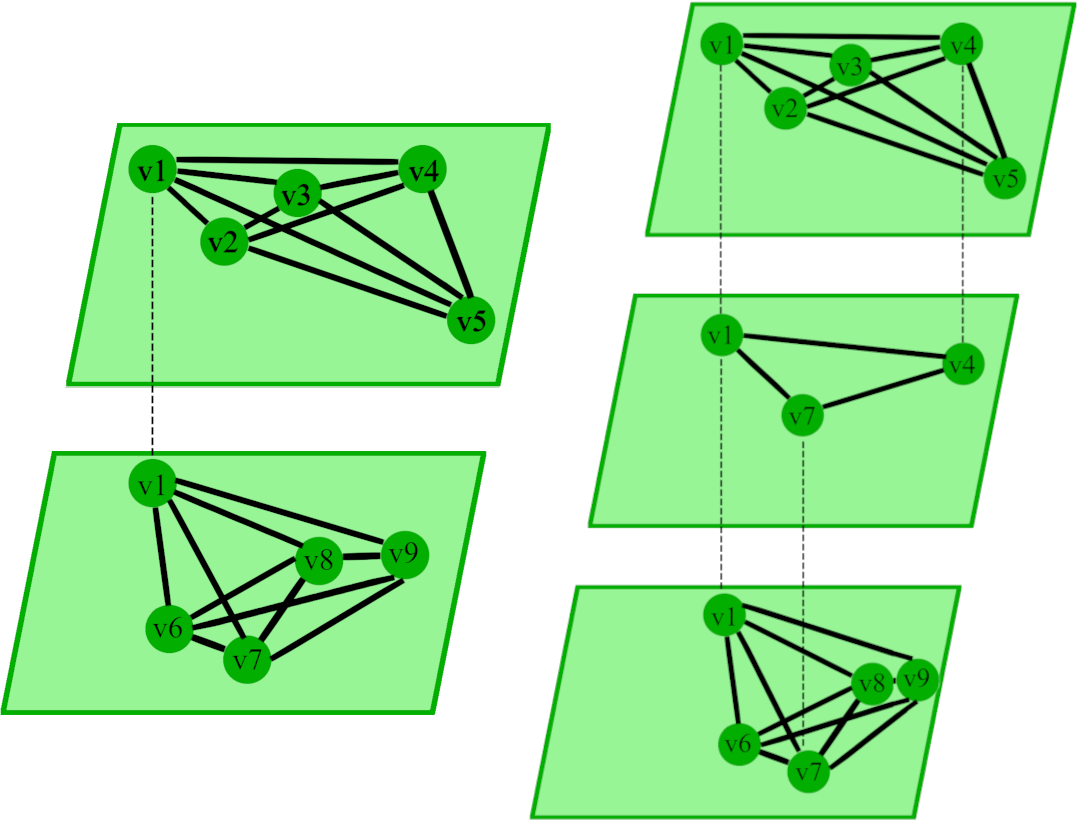Fig.1 (links), Fig.2 (rechts): Hypernetzwerk; eigene Graphik
Falls es einen zusätzlichen Personenkreis gibt, der sich untereinander kennt, wie z. B. ein Arbeitskollege und ein Familienmitglied, erhalten diese ihre eigene Ebene. Auch hier werden die Knoten aus den unterschiedlichen Ebenen mit sich selbst verbunden. (Fig.2)
4. Zusammenfassung
In der Arbeit wurden Beispiele von Multilayer-Netzwerken verschiedener Natur präsentiert. Dadurch wurde gezeigt, dass man zwischen verschiedenen Implementationen unterscheiden kann, oder in gewissen Fällen auch sollte. Aufgrund ihrer unterschiedlichen Charakteristiken kommen diese in verschiedenen Anwendungsbereichen zum Einsatz. Jedoch ist es schwer einen klaren Konsens, der Multilayer-Netzwerke kategorisiert, zu erreichen, da dieses Thema noch sehr jung ist und es viele parallel laufende Arbeiten gibt.
Grob können die Implementationen in 2 Arten aufgeteilt werden. Die einen lassen sich aus Kanten gefärbten Graphen und die anderen als Knoten gefärbten Graphen bilden. Bei diesen liegt eine Knoten und Kanten Heterogenität vor.
Interdependete Netzwerke eignen sich vor allem dazu, Abhängigkeiten zwischen Subsystemen eines komplexen Systems zu modellieren. Das Multiplex Netzwerk ist vor allem dort von Vorteil, wo der Datensatz auf mehrere Schichten aufgeteilt werden kann, um präzisere Ergebnisse in der Analyse zu erhalten. Das Multitype Netzwerk ermöglicht es Vermischungen zwischen den Knoten zu modellieren und Wahrscheinlichkeiten von Verbindungen darzustellen, um weitaus komplexere Vorhersagen treffen zu können. Das Multilevel Netzwerk ist vor allem in Bereichen von Bedeutung, in denen ein Ablauf eines Prozesses dargestellt werden soll, da mithilfe dieser Darstellung bildlich auf jedem Layer ein weiteres Level des Prozesses erreicht wird.
So zeigt sich, warum Multilayer Netzwerke momentan ein Frontier in der Netzwerkanalyse darstellen. Diese bieten ein neues Level an Komplexität, während sie ebenso als eine hoffnungsvolle, neue Alternative zur Modellierung komplexerer, unlimitierter Systeme gesehen werden. Jedoch sollte die Festhaltung und Sammlung der Terminologie und Klassifizierung verschiedener Arten von Multilayer Netzwerken weiter ausgebaut werden, um Arbeiten bezüglich dieses Themas besser finden zu können, um so Forschungsarbeiten zu erleichtern.
5. Referenzen
- Kivela, M., Arenas, A., Barthelemy, M., Gleeson, J. P., Moreno, Y., & Porter, M. A. (2014). Multilayer networks. Journal of Complex Networks, 2(3), 203–271. https://doi.org/10.1093/comnet/cnu016
- Marcello Tomasini. (2015). An Introduction to Multilayer Networks. 3966. https://doi.org/10.13140/RG.2.2.16830.18243
- Porter, M. A. (2018). What Is... a Multilayer Network? Notices of the American Mathematical Society, 65(11), 1. https://doi.org/10.1090/noti1746
- Hammoud, Z., & Kramer, F. (2020). Multilayer networks: aspects, implementations, and application in biomedicine. Big Data Analytics, 5(1). https://doi.org/10.1186/s41044-020-00046-0
- Cardillo, A., Gómez-Gardeñes, J., Zanin, M., Romance, M., Papo, D., del Pozo, F., & Boccaletti, S. (2013). Emergence of network features from multiplexity. Scientific Reports, 3, 1344. https://doi.org/10.1038/srep01344
- Zhao, J., & Lei, X. (2019). Detecting overlapping protein complexes in weighted PPI network based on overlay network chain in quotient space. BMC Bioinformatics, 20(Suppl 25), 682. https://doi.org/10.1186/s12859-019-3256-9
- Odri, S. V., Petrovacki, D. P., & Krstonosic, G. A. (1993). Evolutional development of a multilevel neural network. NEURAL NETWORKS, 6(4), 583–595. https://doi.org/10.1016/S0893-6080(05)80061-9
- Kong, Simonovic, & Zhang. (2019). Resilience Assessment of Interdependent Infrastructure Systems: A Case Study Based on Different Response Strategies. Sustainability, 11(23), 6552. https://doi.org/10.3390/su11236552
- Allard, A., Noël, P.-A., Dubé, L. J., & Pourbohloul, B. (2009). Heterogeneous bond percolation on multitype networks with an application to epidemic dynamics. Phys. Rev. E, 79(3), 036113. https://doi.org/10.1103/PhysRevE.79.036113
- Wang, G., & Li, H. (2009). Color degree and alternating cycles in edge-colored graphs. Discrete Mathematics, 309(13), 4349–4354. https://doi.org/10.1016/j.disc.2009.01.016
- Castet, J.-F., & Saleh, J. H. (2013). Interdependent multi-layer networks: modeling and survivability analysis with applications to space-based networks. PLOS ONE, 8(4), e60402. https://doi.org/10.1371/journal.pone.0060402
- Wang, J., Jiang, C., & Qian, J. (2014). Robustness of interdependent networks with different link patterns against cascading failures. Physica A: Statistical Mechanics and Its Applications, 393, 535–541. https://doi.org/10.1016/j.physa.2013.08.031