Speicheransätze/-optimierung für Multilayer-Netzwerke
| Eric Langen | Nino Menzel | Ergi Isaraj | ||
|---|---|---|---|---|
| RWTH Aachen University | RWTH Aachen University | RWTH Aachen University | ||
| eric.langen@rwth-aachen.de | nino.menzel1@rwth-aachen.de | ergi.isaraj@rwth-aachen.de |
Abstract
Im Zuge der weltweit fortschreitenden Vernetzung gewinnt die Analyse komplexer sozialer Netzwerke zunehmend an Bedeutung. Da sich der Austausch zwischen Menschen selten auf ein einziges Medium beschränkt, wird das Modellieren von komplexen Sachverhalten als Multilayer Netzwerke (MLN) immer wichtiger. Diese eröffnen neue Möglichkeiten, verschiedene Aspekte oder Kommunikationswege darzustellen. So lassen sich beispielsweise Merkmale wie die Zeit und Art einer Interaktion sowie das Alter der Akteure durch die verschiedenen Ebenen repräsentieren.
Die Speicherung und Analyse von Daten mit mehreren Merkmalen ist jedoch insbesondere dann eine Herausforderung, wenn die Daten aufgrund der großen Datenmenge komprimiert werden müssen. Hierbei muss Verlust von Informationen minimiert werden. Dies ist wichtig, um Flexibilität bei der Auswahl der Merkmale für die jeweilige weitere Analyse beizubehalten. Aus diesen Gründen, ist es von großer Bedeutung eine optimale Vereinfachungsmethode zu finden. Dieses Paper soll eine Entscheidungsgrundlage für diese Wahl und einen Überblick über geeignete Methoden bieten. Es werden drei verschiedene Methoden vorgestellt, welche dieses Problem auf verschiedene Weise lösen und für welche weiteren Analyseziele diese geeignet sind. Unsere experimentellen Ergebnisse zeigen, wie verschieden stark die Methoden die Netzwerke verkleinern und welche Auswirkungen dies auf die Weiterverarbeitung der Daten hat.
___
Inhaltsverzeichnis
1. Einleitung
In realen Netzwerken gibt es in der Regel mehrere Arten von Interaktionen (Kanten) zwischen Akteuren (Knoten), zum Beispiel können die Beziehungen zwischen zwei Nutzern in einem sozialen Netzwerk Freunde, Kollegen, Verwandte usw. sein. Die Akteure und Interaktionen werden in der Regel als mehrschichtiger Graph modelliert, wobei jede Schicht eine bestimmte Art von Interaktion zwischen den Akteuren erfasst. Jedoch führt die Verfügbarkeit riesiger Mengen komplexer Netzwerkdaten unweigerlich zu Problemen bei der Verarbeitung. Die Modellierung dieser Netzwerke in ihrer Gesamtheit zu Analysezwecken ist in den meisten Fällen nicht durchführbar und die Konzentration auf begrenzte Teile des Netzwerks führt häufig zu Problemen bei der Spezifikation der Grenzen (Kossinets, 2006) (Laumann et al., 1989).
Die Vereinfachung von MLN kann zusätzlich die Leistung weiterer rechnerischer Analysemethoden verbessern, welche Probleme mit der Handhabung sehr großer Netzwerke haben können.
Für die Speicherung von MLN gibt es Optimierungsmethoden, welche den benötigten Speicher deutlich reduzieren können. Drei Methoden werden wir im Folgenden genauer erörtern. So werden wir Methoden zur Zusammenfassung eines MLN zum Generieren eines kompakteren MLN, zur Speicherung eines MLN als Vektorraum und zur Berechnung der innenliegensten Teilgraphen erläutern, anwenden und evaluieren. Diese haben für verschiedene Arten der Weiterverarbeitung jeweils Vorteile, welche zur Auswahl der Richtigen Methode für den jeweiligen Anwendunsfall relevant sind.
2. Verwandte Arbeiten
Das Paper “Multilayer network simplification” stellt eine einheitliche und praktische Taxonomie der bestehenden Vereinfachungsansätze vor und identifiziert unterentwickelte Kategorien von Vereinfachungsmethoden für MLN (Interdonato et al., 2020). Bei den Kategorien handelt es sich zunächst um die Gruppierung, welche durch die Paper “Efficient Aggregation for Graph Summarization” und “Scalable Pattern Matching over Compressed Graphs via Dedensification” vertreten wird. Die Autoren Yuanyuan Tian, Richard A. Hankins und Jignesh M. Patel stellen zwei Methoden vor, die intuitiv und leicht kontrollierbar die ‘Graph Summarization’ ausführen können. Mittels diesen Methoden kann von mehreren Knotenattributen und Beziehungen der Knoten ausgewählt werden, um dann eine Zusammenfassung dieser zu ermöglichen (Tian et al., 2008). Antonio Maccioni und Daniel J. Abadi hingegen führen ein Verfahren ein, welches darauf abzielt, eine Erhöhung der Leistung beim skalierbaren Abfragen in Datenbanken zu bringen. Die Anwendungen dieser Methode befinden sich vorwiegend in dem Bereich von Graphdatanebanken (Maccioni & Abadi, 2016). Die zweite Kategorie handelt von der Transformation von Graphen. In dieser wird großer Wert auf Embedding Methoden gelegt, welche in unserem Paper durch den Algorithmus “Node2Vec” repräsentiert wird. An Node2Vec wurde geforscht, um einen Algorithmus basierend auf Random Walks zu erlangen, bei dem durch Parameter, Einfluss auf die jeweiligen Random Walks ausgeübt werden kann (Grover & Leskovec, 2016). Bei der dritten und letzten Kategorie handelt es sich um die Selektion. Die letzte Kategorie ist die Selektion, wobei hier auf das Konzept der Multilayer-core-decomposition eingegangen wird. Die Paper “CoreCube: Core Decomposition in Multilayer-Networks” (Liu et al., 2020) und “Core Deconposition in Multilayer Networks: Theory, Algorithms and Application” behandeln beide die core-decomposition auf Mulilayer-Netzwerken und Methoden zu dessen Berechnung.
3. Methodik
Methoden der Vereinfachung von Multilayer-Netzwerken lassen sich nach (Interdonato et al., 2020) in die drei Kategorien Gruppierung, Transformation und Selektion aufteilen. Deren Funktionsweise sowie die mögliche Speicherung deren Ergebnisse wird im Folgenden erörtert.
3.1 Gruppierung
Gruppierung bezieht sich auf Techniken, die dafür eingesetzt werden, ein kompakteres MLN zu erzeugen, um darauf komplexe Algorithmen arbeiten zu lassen oder wichtige Informationen mit minimalem Datenverlust abzuleiten. Hierzu existieren verschiedene Methoden, von denen wir uns in diesem Paper auf zwei fokussieren werden, welche im Kontext der Speicheroptimierung besonders relevant sind.
Graph Summarization durch Aggregation
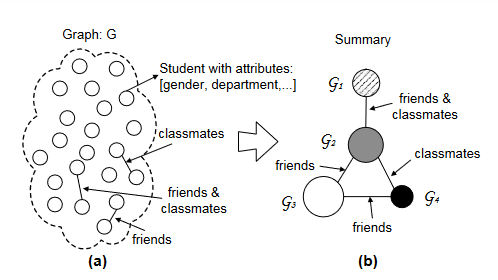
Es handelt sich bei Graph Summarization um ein Vereinfachungsverfahren, welches darauf abzielt, die wichtigste strukturelle Eigenschaften eines Netzwerkes zusammenzufassen. Dies ermöglicht eine sehr einfache weitere Analyse des Graphen, welche sonst bei häufig sehr großen Knoten- und Kantenmengen sehr aufwendig gewesen wäre. Aus diesem Grund muss die Information aus dem Graphen extrahiert und erfasst werden.
In diesem Abschnitt wird die Operation SNAP (Summarization by Grouping Nodes on Attributes and Pairwise Relationships) betrachtet, da wir eine Implementierung dieser Methode in Python verwenden. Ihr Ziel ist es, kleine, kompakte und informative Zusammenfassungen der Eigenschaften in Graphen zu erstellen. Die von dem Nutzer ausgewählten Knotenattribute oder Knotenbeziehungen werden von SNAP berücksichtigt und daraus wird der sogenannte “Summary Graph”, also die Zusammenfassung, generiert.
Im Folgenden definieren wir einige Begriffe, um dann eine mathematische Darstellung der SNAP Operation zu ermöglichen.
Definition 1: Node-Gruppierung eines Graphes
Sei \(G\) ein Graph. Wir nennen \(\Phi\) = {\(G_1\), \(G_2\), …, \(G_k\) } die Knoten-Gruppierung eines Graphes genau dann, wenn:
1) \(\forall G_i \in \emptyset\), \(G_i \subseteq V(G)\) und \(G_i \neq \emptyset\)
2) \(\bigsqcup_{G_i \in \Phi} G_i = V(G)\)
3) for \(\forall G_i, G_j \in \Phi\) and \((i \neq j), G_i \cap G_j = \emptyset\)
Definition 2: Dominance Relation
Sei \(G\) ein Graph. Die Gruppierung \(\Phi\) dominiert \(\Phi^{'}\), bezeichnet als \(\Phi^{'}\) < \(\Phi\), genau dann, wenn \(\forall G_{i}^{'} \in \Phi^{'} \exists G_j \in \Phi\) sodass \(G_{i}^{'} \subseteq G_{j}\). (Tian et al., 2008)
Definition 3: A-kompatible Gruppierung
Sei \(A\) eine Menge von Attributen. Die Gruppierung \(\Phi\) ist mit \(A\) kompatibel oder auch \(A\)-kompatibel, wenn \(\forall u,v \in V, if \Phi (u) = \Phi (v)\) , then \(\forall a_i \in A, a_{i}(u) = a_{i}(v)\). (Tian et al., 2008)
Theorem 1
In der Menge der allen \(A\)-kompatiblen Gruppierungen von \(G\), bezeichnet als \(S_A\), \(\exists \Phi_A \in S_A\) sodass \(\forall \Phi_{A}^{'} \in S_A, \Phi_{A}^{'} < \Phi_A\).
Der zugehörige Beweis wird von Yuanyuan Tian in dem Paper “Efficient aggregation for graph summarization” erbracht (Tian et al., 2008).
Definition 4: Attribut und Beziehungen kompatibel Gruppierung
Sei \(A\) eine Menge von Attributen und \(R\) eine Menge von Beziehungen zwischen Knoten. Eine Gruppierung \(\Phi\) ist Attribut und Beziehungen kompatibel, bezeichnet als \((A, R)\)-kompatibel, wenn:
1) \(\Phi\) ist \(A\)-kompatibel
2) \(\forall u,v \in V(G)\) , wenn \(\Phi (u) = \Phi (v)\) , dann \(\forall E_i \in R, NeighbourGroups_{\Phi, E_i}(u) = NeighbourGroups_{\Phi, E_i}(v)\) \
\(NeighbourGroups_{\Phi, E_i}(v)\) = {\(\Phi (u) | (u,v) \in E_i\)} (Tian et al., 2008)
Theorem 2:
In der Menge aller \((A,R)\)-kompatiblen Gruppierungen von \(G\), bezeichnet als \(S_{(A,R)}\), \(\exists \Phi_{(A,R)} \in S_{(A,R)}\) sodass \(\forall \Phi_{(A,R)}^{'} \in S_{(A,R)}, \Phi_{(A,R)}^{'} < \Phi_{(A,R)}\).
Der zugehörige Beweis wird von Yuanyuan Tian in dem Paper “Efficient aggregation for graph summarization” erbracht (Tian et al., 2008).
Definition 5: SNAP Operation
Die SNAP Operation nimmt als Eingabe den Graph G, eine Menge von Attributen und eine Menge von Beziehungen zwischen Knoten an und gibt eine Zusammenfassung zurück, wobei V(\(G_{snap}\)) = \(\Phi_{(A,R)}^{max}\) und Y(\(G_{snap}\)) = { \(E_i(G, \Phi_{(A,R)}^{max})\) sodass \(E_i \in R\) } (Tian et al., 2008)
3.2 Transformation
Speicheroptimierung durch Transformation befasst sich mit der Änderung einer Anzahl von Objekten in einem Graphen. Allgemein verständlich ausgedrückt, werden in dieser Methode Objekte aus einem Graphen entfernt, transformiert und anschließend wieder in den Graphen zurück eingesetzt. Im weiteren Verlauf wird auf eine Embedding Methode eingegangen, da diese sich besonders zur Speicheroptimierung eignet.
Embedding
Techniken zur Einbettung von Graphen sind ein hilfreiches Werkzeug bei der Umwandlung hochdimensionaler, spärlicher Graphen in niedrig dimensionale, dichte und kontinuierliche Vektorräume, wobei die Eigenschaften der Graphenstruktur weitestgehend erhalten bleibt (Xu, 2021). Die daraus entstehenden Vektorräume sind um einiges speichereffizienter und auf ihnen lassen sich maschinelle Algorithmen, wie zum Beispiel link prediction oder community detection, einfacher anwenden. Auch zur Visualisierung von gigantischen Graphen eignet sich die Generierung von Knoten-Einbettung.
Viele Algorithmen zu Graphen-Einbettung basieren auf sogenannten Random Walks, welche die Nachbarschaft eines Knoten \(n\) repräsentieren. Ein bekannter Algorithmus basierend auf diesem Prinzip ist der Node2Vec, welcher mithilfe von Random Walks und dem Skip-gram-Modell Knoten-Einbettungen berechnet. DeepWalk und LINE sind weitere nennenswerte Algorithmen, basiert auf Random Walk.
Im Allgemeinen funktioniert ein Random Walk so, dass von einem bestimmten Startpunkt \(u\) ein Pfad der Länge \(l\) gebildet wird, indem \(c_i\) den \(i\)-ten Knoten im Pfad angibt, angefangen mit \(c_0 = u\). Die Noten werden nach der folgenden Verteilung generiert (Grover & Leskovec, 2016):
Hierbei ist \(\pi_{vx}\) die nicht normalisierte Übergangswahrscheinlichkeit von dem Knoten \(v\) zu dem Knoten \(x\), \(Z\) die normalisierungs Konstante und \(E\) die Menge aller Kanten.
Um die Übergangswahrscheinlichkeit der Knoten zu berechnen, wurde es bei Node2Vec vermieden, diese gleich der Kantengewichte zu setzen (\(\pi_{vx} = w_{vx}\)), da dies keine Möglichkeit bietet Random Walks zu leiten. Stattdessen wurde sich ein Random Walk zweiter Ordnung mit zwei Parametern definiert. Anhand der zwei Parameter, lässt sich kontrollieren, ob sich die Random Walks eher in nächster Nachbarschaft, oder möglichst weit weg vom Startpunkt ausbreiten. Die Übergangswahrscheinlichkeit wird anhand eines such bias \(\alpha\) berechnet, mit \(\pi_{vx} = \alpha(t, x) * w_{vx}\), wobei \(\alpha\) folgender derart wird (Grover & Leskovec, 2016):
\(\alpha_{pq}(t, x) = \begin{cases} \frac{1}{p} &\text{if } d_{tx} = 0\\ 1 &\text{if } d_{tx} = 1\\ \frac{1}{q} &\text{if } d_{tx} = 2 \end{cases}\)
\(d_{tx}\) vertritt dabei den Abstand von Knoten t zu Knoten x.
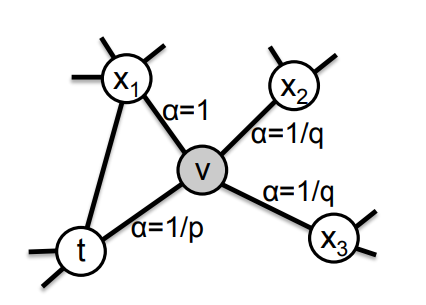(Grover & Leskovec, 2016)
Ein beispielhafter Walk, bei dem gerade die Kante \((t, v)\) gelaufen wurde
Der Parameter \(p\) gilt als Return Parameter. Wird dieser Parameter groß gesetzt (\(> max(q, 1)\)) ist es unwahrscheinlicher, zu einem bereits besuchten Knoten zurückzukehren. Setzt man p klein (\(< min(q, 1)\)), ist es wahrscheinlich zum vorherigen Knoten zurückzugehen (Grover & Leskovec, 2016).
Der In-out Parameter \(q\) erlaubt es einem, die Übergangswahrscheinlichkeit für Knoten nahe dem Startpunkt zu manipulieren. Setzt man diesen Parameter \(q > 1\), so steigt die Wahrscheinlichkeit Knoten in der Nähe das Startknoten zu besuchen. Wird \(q < 1\) gesetzt, so steigt die Wahrscheinlichkeit zu einem fernen Knoten zu gehen (Grover & Leskovec, 2016).
Nach Generierung der Random Walks werden diese mithilfe des Skip-gram Modells in einen \(d\) dimensionalen Vektorraum umgerechnet. Das Skip-gram Modell besteht aus einem neuronalen Netzwerk, welches für ein Eingabewort die Wahrscheinlichkeit für ein anderes zutreffendes Wort vorhersagt. Im Falle der Random Walks werden die Knoten als Wörter angesehen und die Walks als Sätze.
Node2Vec lässt sich auf (un-)gewichtete, sowie (un-)gerichtete Graphen anwenden, allerdings bietet der Algorithmus keine Funktionsweise für Multilayer Netzwerke. Aus Grund dessen, gibt es mehrere Möglichkeiten, wie man Multilayer Netzwerke mithilfe von Node2Vec einbettet. Drei sinnvolle Lösungen werden im Paper PMNE (Principled multilayer network embedding) vorgestellt (Liu et al., 2017).
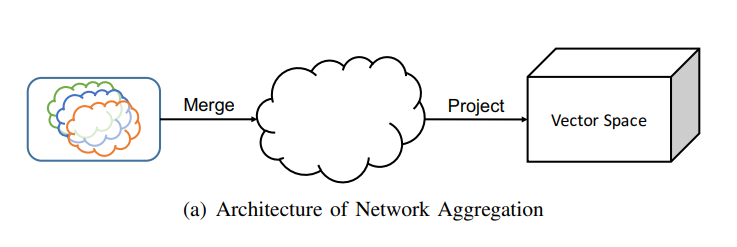
Architecture of Network Aggregation
Die erste Möglichkeit, die sich uns anbietet, besteht darin, die einzelnen Layer des Graphen zunächst zusammenzuführen und anschließend mit Node2Vec in einen Vektorraum umzurechnen.
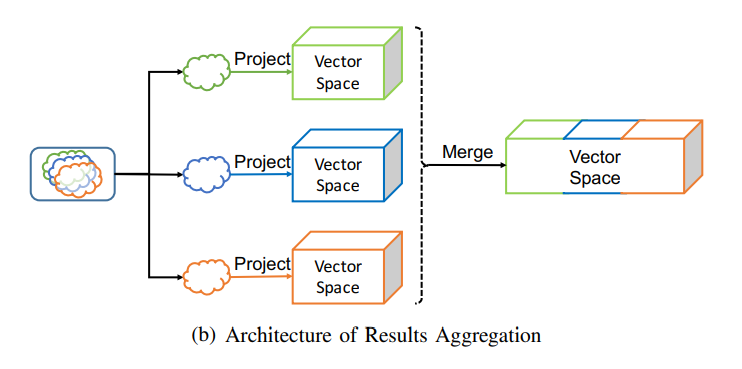
Architecture of Results Aggregation
Es lassen sich gleichermaßen konträr zur ersten Methode, die einzelnen Layer als Erstes mit Node2Vec in Vektorräume umwandeln und anschließend diese zusammenführen.
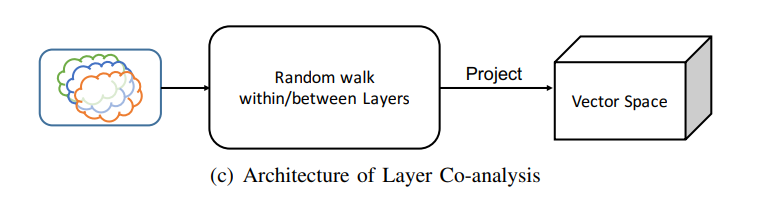
Architecture of Layer Co-analysis
Anstatt die Random Walks auf den einzelnen Ebenen zu begrenzen, lässt sich auch ein Multilayer Netzwerk anhand von Layer übergreifenden Random Walks in einen Vektorraum überführen.
3.3 Selektion
In diesem Abschnitt beschäftigen wir uns stellvertretend für die Selektion mit dem nach Roberto Interdonato der Selektion untergeordneten Konzept der Filterung. Für die Filterung nutzen wir die Kernzerlegung (\(k\)-core decomposition), welche auf dem Konzept der degree centrality basiert (Interdonato et al., 2020). Die \(k\)-core-decomposition ist eine der am besten untersuchten Graphenzerlegungen, beziehungsweise Filteransätze und besteht darin, die Kernzahl für jeden Knoten im Graphen zu berechnen. Sie ist ein leistungsfähiges Instrument zur Modellierung der Dynamik des Nutzerverhaltens in sozialen Netzwerken, da ein Nutzer dazu neigt, ein neues Verhalten anzunehmen, wenn es eine beträchtliche Anzahl von Freunden (z.B. die Kernzahl dieses Nutzers) in der Gruppe gibt, welche das gleiche Verhalten angenommen haben (Malliaros & Vazirgiannis, 2013). In einem einschichtigen Graphen kann man die Kernzahl eines Knotens berechnen, indem man k hochzählt und nacheinander alle Knoten, welche einen Grad kleiner als \(k\) haben, und die mit ihnen verbundenen Kanten entfernt. Die Kernzahl eines Knotens ist dann das \(k\), bei welchem er entfernt wurde, minus eins. Der \(k\)-Kern ist dann der maximale durch die Knoten mit dieser Kernzahl induzierte Teilgraph. Der multilayer \(k\)-core wird durch den coreness vector, einen \(\mid L\mid\) -dimensionalen Vektor \(k=[k_l]_{l \in L}\) charakterisiert, wobei \(\mid L\mid\) die Anzahl der Ebenen des Graphen ist, dessen Komponenten \(k_l\) den minimalen Grad darstellen, den ein Knoten in der \(l\)-ten Schicht haben muss, um in diesem \(k\)-Kern zu sein (Galimberti et al., 2020).
Definition 1: Multilayer k-core
Bei einem Multilayer-Netzwerk \(G = (V,E,L)\), einer Menge von Ebenen \(L' \subseteq L\) und einer ganzen Zahl \(k\) ist der multilayer \(k\)-core von \(G\) auf \(L'\), notiert als \(C_L^k\), die maximale Knotenmenge, sodass jeder Knoten \(v\) in dem von \(C_L^k\) induzierten Teilgraphen \(H\) die Bedingung \(deg_H(v,l)\ge k\) für jedes \(l \in L'\) erfüllt(Liu et al., 2020).
Definition 2: Kernzahl
Bei einem Multilayer-Netzwerk \(G=(V,E,L)\) und mit Menge von Ebenen \(L'\subseteq L\), ist die Kernzahl von \(v\) auf \(L'\), bezeichnet mit \(C_{L'}(v)\), das größte \(k\), sodass \(v\) im multilayer \(k\)-core auf \(L'\) enthalten ist, d.h. \(C_{L'} = \text{max}\{k | v \in C^k_L\}\)(Liu et al., 2020).
Definition 3: Multilayer core decomposition
Bei einem Multilayer-Netzwerk \(G = (V,E,L)\) und einer Menge von Ebenen \(L' \subseteq L\) berechnet die Multilayer core decomposition, bezeichnet mit \(C_{L'}\), \(C_L^k\) für alle \(1 \le k \le k_{\text{max}}\)(Liu et al., 2020).
Definition 4: Lattice Level
Das Lattice Level \(i\) enthält alle Kerne bei welchen die Summe über die Komponenten ihres coreness Vektors \(i\) ergibt (Galimberti et al., 2020).
Definition 5: \(l_r\)-right-inner-most Multilayer Cores
Bei einem multilayer Graphen \(G = (V,E,L)\) und einer Schicht \(l_r \in L\) entsprechen die \(l_r\)-right-inner-most Multilayer Cores eines Kernes \(C_k\) von \(G\), wobei \(k = [k_l]_{l \in L}\) ist, allen Kernen von \(G\) mit dem coreness Vektor \(k'=[k'_l]_{l \in L}\), so dass \(\forall l \in [l_1,l_r):k'_l=k_l\) und es keinen anderen Kern mit dem coreness Vektor \(k''=[k''_l]_{l\in L}\) gibt, so dass \(\forall l \in [l_1,l_r):k''_l=k_l, \forall l \in [l_r,l_{\mid L \mid}]:k''_l \ge k'_l\) und \(\exists \hat l \in [l_r,l_{\mid L \mid }]:k''_{\hat l}>k'_{\hat l}\) (Galimberti et al., 2020) .
Nach Edoardo Galimberti ist man die Definition für die \(l_r\)-right-inner-most Multilayer Cores äquivalent zu der inner-most cores, jedoch lässt sie sich leichter implementieren (Galimberti et al., 2020). Inner-most cores sind jene cores, bei welchen man keine Komponente des coreness vectors erhöhen könnte, ohne dass sie leer werden. Diese sind besonders interessant, weil sie meist um Größenordnungen kleiner sind, als der ursprüngliche Graph (Galimberti et al., 2020). Hierbei gilt es jedoch zu beachten, dass nicht zwingend eine Verkleinerung stattfinden muss, da Netzwerke mit einer sehr hohen average-degree density sehr große inner-most cores haben, welche zusammengenommen die Größe des ursprünglichen Netzwerkes übersteigen können. Deswegen ist diese Methode nicht immer geeignet.
In dem Paper “Core Decomposition in Multilayer Networks: Theory, Algorithms, and Applications” wird ein Algorithmus zur direkten Berechnung der inner-most Multilayer Cores vorgeschlagen (Galimberti et al., 2020). Dieser teilt sich in die im Paper als Algorithmen IM-ML-cores (innermost-multilayer-cores) und RIM-ML-cores (right-inner-most-cores) bezeichneten Algorithmen auf, wobei der IM-ML-cores Algorithmus für die Rekursion und der RIM-ML-cores Algorithmus für die tatsächliche Berechnung zuständig ist. Dieser nutzt aus, dass die Menge aller \(l_1\)-right-inner-most multilayer cores äquivalent zu allen inner-most multilayer cores ist und berechnet die \(l_r\)-right-inner-most multilayer cores rekursiv. Hierbei beginnt er mit der Wurzel des core lattice. Der Algorithmus verwendet eine Datenstruktur \(\mathcal M\), welche aus einer Reihe von verschachtelten Abbildungen, eine für jede Ebene bis auf die letzte, besteht. Für jede bereits bearbeitete Ebene wird in \(\mathcal M\) der minimale Grad gespeichert, den ein core in der Ebene \(l_r\) haben muss, um inner-most zu sein. Gegeben ein coreness vector \(k\) und eine Ebene \(l_r\), wird durch den Befehl \(\mathcal M (k,l_r)\) über die verschachtelten Abbildungen mithilfe der Elemente in \(k\) als Schlüssel bis zur Ebene \(l_r\) iteriert.
(Galimberti et al., 2020)
Mithilfe der multilayer core decomposition lässt sich wie von Edoardo Galimberti beschrieben auch eine approximierte Lösung des Multilayer Densest Subgraph Problems sowie eine mehrschichtige Community Suche umsetzen, weswegen diese Methode der Netzwerkvereinfachung für viele Anwendungen sinnvoll ist (Galimberti et al., 2020). Je nach Anwendung wählt man anhand bestimmter Parameter oder weiteren Algorithmen geeignete Kerne aus, welche dann einen Bruchteil der Kanten und Knotenzahl des ursprünglichen Graphen haben und so signifikant weniger Speicherplatz benötigen und trotzdem die gewünschten Eigenschaften für die Weiterverarbeitung beibehalten. So kann man neben der Berechnung der innenliegensten Kerne auch das Lattice Level erhöhen, welches die resultierenden Kerne mindestens haben müssen. So erhöht man den geforderten Grad, den die Knoten haben müssen, um im Kern zu bleiben und kann so die Anzahl der Knoten beliebig weit reduzieren. Hierbei verliert man natürlich mehr Informationen, je höher man das Lattice Level wählt.
4. Anwendung
4.1 Anwendung SNAP
Hier wenden wir den SNAP-Algorithmus auf einen Datensatz an, welcher politische Blogbeiträge und Interaktionen beschreibt. Nach einer kurzen Beschreibung des gewählten Datensatzes, evaluieren wir in diesem Abschnitt den SNAP-Algorithmus, indem die wichtigen Eigenschaften des Graphen mit der von Lada A. Adamic und Natalie Glance entwickelten Analyse evaluiert werden (Adamic & Glance, 2005).
4.1.1 Dataset
Unserer gewählter Datensatz heißt “Political Blogs Dataset” (Adamic & Glance, 2005) und kann aus dieser Quelle heruntergeladen werden, http://www-personal.umich.edu/~mejn/netdata. Darin enthalten ist ein Netzwerk von 1490 Blogbeiträgen mit Fokus auf die US-Wahl im Jahr 2004 und 19090 Hyperlinks zwischen diesen Beiträgen. Das heißt jeder Knoten in unserem Netzwerk entspricht einem Blogbeitrag und jede Kante einem Hyperlink. Außerdem hat jeder Knoten eine Eigenschaft, welche die politische Richtung des Beitrages vermutet. Ein Blogpost ist somit entweder “Liberal” oder “Konservativ”.
Nun listen wir die wichtigsten Folgerungen aus der Analyse (Adamic & Glance, 2005) auf, sodass wir einen nominalen Vergleich zu den grundlegenden strukturellen Eigenschaften unseres gewählten Datensatzes durchführen können. Es werden die unten stehenden Folgerungen gezogen:
- Es gibt weniger Hyperlinks zwischen den beiden politischen Gruppen als in den jeweiligen Gruppen
- “Konservative”-Beiträge verweisen tendenziell öfter auf andere Beiträge als “Liberale”-Beiträge
- Die “Konservative”-Sphäre ist dichter in sich verlinkt als die “Liberale”-Sphäre
4.1.2 Evaluation
Nach der Anwendung von dem SNAP-Algorithmus auf unseren Datensatz erhalten wir folgenden Graphen:
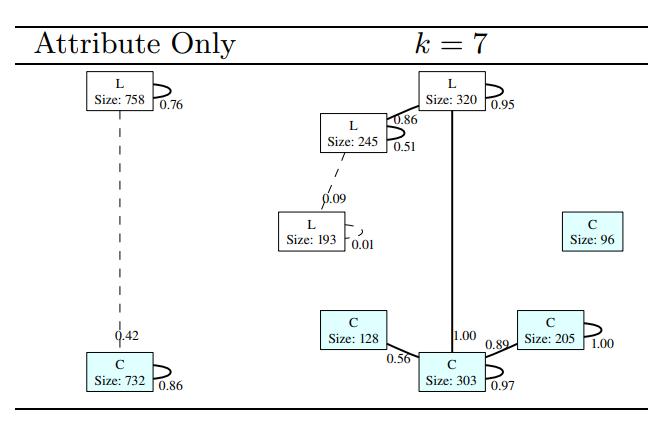(Tian et al., 2008)
Dies ist also der “Summary Graph”, den wir zunächst untersuchen, damit wir prüfen können, ob die Hauptfolgerungen aus der Analyse (Adamic & Glance, 2005) auch hier gelten. Ist das der Fall, dann haben wir eine sinnvolle Zusammenfassung der wichtigsten zugrundeliegenden Eigenschaften erstellt.
In der Ausgabe sind die Kanten gewichtet, was dazu dient, die Dichte der Hyperlinks zwischen den Gruppen anzugeben. Diese ist beim Visualisieren oder bei einer quantitativen Analyse hilfreich. Es lässt sich aus dem “Summary Graph” schließen, dass die beiden politischen Sphären in sich starker miteinander verlinken. Zudem wird es durch die Gewichte gezeigt, dass die “Konservativen”-Beiträge häufiger auf andere Blogbeiträge verlinken. Diese sind aber auch dichter verlinkt, da das Gewicht der selbst führenden Kante der “C”-Knoten größer als das von der zu sich führenden Kante der “L”-Knoten.
Daher gelten alle Folgerungen aus der Analyse von Lada A. Adamic und Natalie Glance (Adamic & Glance, 2005) auch in unserem “Summary Graph”. Aus diesem Grund kann man schließen, dass die Zusammenfassung sinnvoll ist.
4.2 Anwendung Node2Vec
Für die Anwendung von Node2Vec haben wir das Pythonpaket Node2Vec verwendet, mit dessen Hilfe wir den Algorithmus auf unseren Networkx Graphen anwenden konnten. Unser Graph stammt aus dem Datensatz eines sozialen Netzwerkes der Universität von Kalifornien (https://snap.stanford.edu/data/CollegeMsg.html). Aus diesem Datensatz wurden die privaten Nachrichten als Graph dargestellt, wobei die Personen als Knoten und Nachrichten als Kanten repräsentiert werden. Des Weiteren ist ein UNIX Zeitstempel der Nachrichten angegeben, welchen wir für unsere Zwecke dekodiert und die einzelnen Tage Layer repräsentieren haben. Der Graph ist ungewichtet und ungerichtet. Um Node2Vec anzuwenden, greifen wir auf die in der Methodik erklärten Architecture of Network Aggregation zurück und führen alle Ebenen zusammen, bevor wir anschließend Node2Vec darauf laufen lassen. Zunächst hier eine bildliche Darstellung des Graphen:
Lassen wir nun unseren Algorithmus über den Graphen laufen, mit der Dimension \(d = 16\), einer Länge der Walks von \(l = 80\) und mit \(10\) Walks pro Knoten, erhalten wir unsere eingebettete Datei. Unser Graph, mit einem Speicherplatz von 540 KB, wurde soeben in einen Vektorraum mit einem Speicheraufwand von lediglich 331 KB umgerechnet. Wir Menschen können uns allerdings kaum etwas unter lauter Zahlen vorstellen, weshalb wir den Vektorraum runter dimensionieren. Darstellen lässt sich das ganze mithilfe des Matplotlib Paketes.
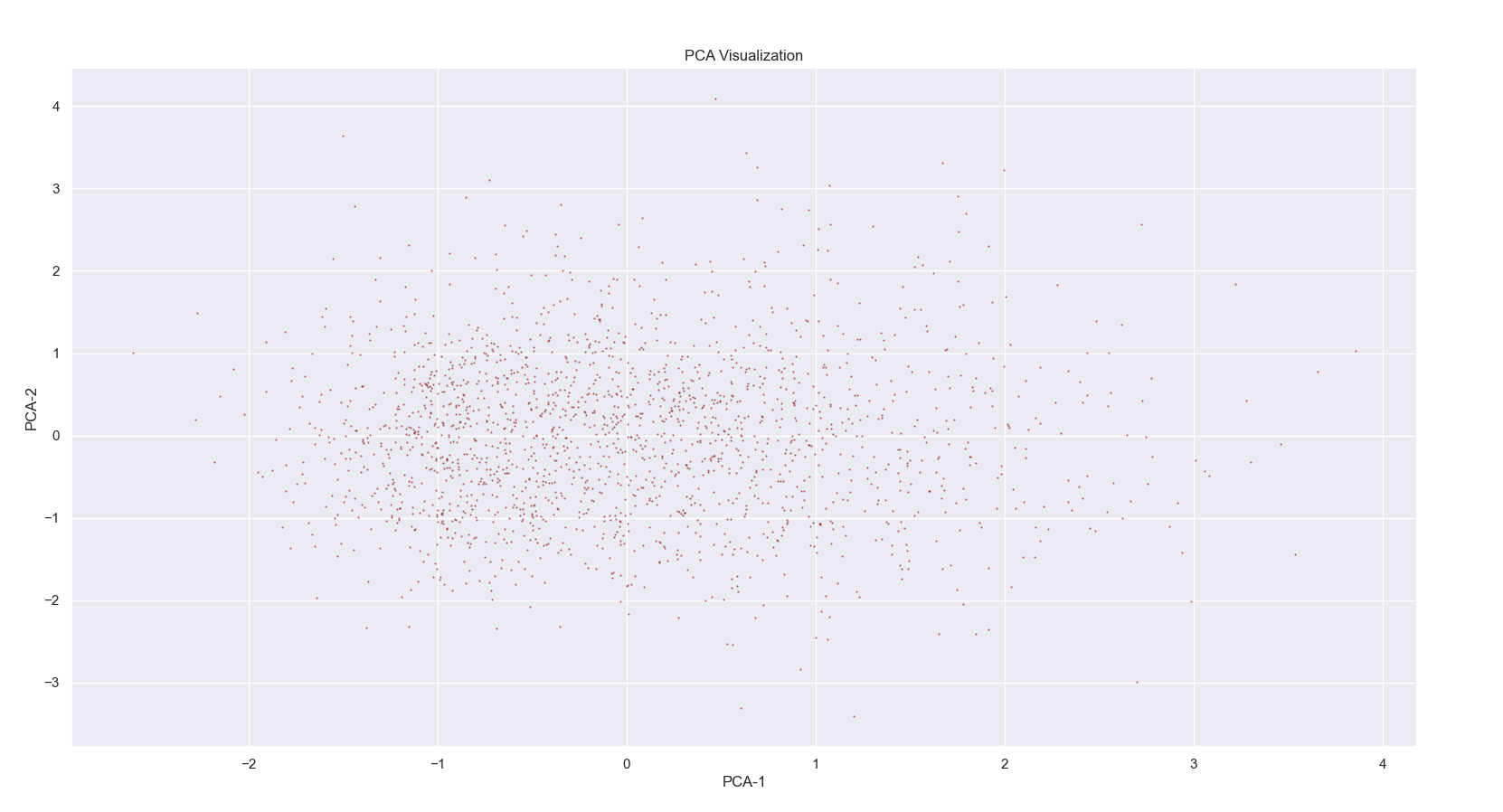
Mit diesem Vektorraum können maschinelle Algorithmen erheblich einfacher und effizienter arbeiten, da sich der Graph jetzt in einer numerischen Darstellung befindet. Jeder Punkt repräsentiert einen Knoten im Graph, besser gesagt eine Person. Punkte, die sich ähneln im Graphen, liegen nahe beieinander, hierbei ist die Bedeutung der Achsen zunächst irrelevant. Es lassen sich am Vektorraum Clusterbildungen um Personen mit ähnlichem Chatverhalten, im Sinne von einem Nachrichtenaustausch zwischen denselben Studenten, oder kurzerhand Freundesgruppen erkennen.
In näherer Zukunft wird die Bedeutung von Algorithmen, wie Community detection oder link prediction, weiterhin steigen. Die Forschung an Einbettungs-Methoden wäre daher von erheblichem Vorteil. Nicht nur die Präzision, sondern auch die Laufzeitgeschwindigkeit könnte somit gesteigert werden.
4.3 Anwendung Multilayer core decomposition
Die Multilayer core decomposition haben wir mithilfe des von Edoardo Galimberti und seinen Co-Autoren zur Verfügung gestellten Codes (https://github.com/egalimberti/multilayer_core_decomposition) auf drei Datensätze angewendet, welche unter anderem auch in demselben Paper untersucht werden (Galimberti et al., 2020). Zwei der Datensätze stellen jeweils verschiedene genetische Interaktionen zwischen Genen im Menschen (Homo Sapiens) (Galimberti et al., 2020) und Saccharomyces Cerecisiae (eines Hefepilzes) (Galimberti et al., 2020) dar. Der dritte hier betrachtete Datensatz ist das DBLP Netzwerk (Bonchi et al., 2015), welches ein Co-Autorennetzwerk ist, bei welchem zwei Autoren von einer Kante verbunden sind, wenn sie an einer wissenschaftlichen Veröffentlichung zusammengearbeitet haben. Die Ebenen entsprechen zehn ausgewählten Themenbereichen und eine Kante liegt auf ihr, wenn sie in diesen Themenbereich passt. Die Datensätze werden im folgenden mit Homo, SacchCere und DBLP abgekürzt.
Eigenschaften der Datensätze: Anzahl Knoten; Anzahl der Kanten; Anzahl der Ebenen; minimale, durchschnittliche und maximale Knotenzahl auf einer Ebene
| Datensatz | \(\mid V \mid\) | \(\mid E \mid\) | \(\mid L \mid\) | min \(\mid E_l\mid\) | avg \(\mid E_l \mid\) | max\(\mid E_l \mid\) | average degree-density |
|---|---|---|---|---|---|---|---|
| Homo Sapiens | 18.000 | 153.000 | 7 | 256 | 21.000 | 83.000 | 8,45 |
| SaccCere | 6.500 | 247.000 | 7 | 1.300 | 35.000 | 91.000 | 37,62 |
| DBLP | 513.000 | 1.000.000 | 10 | 96.000 | 101.000 | 113.000 | 1,98 |
Die Ausführung des Algorithmus zur Berechnung der inner-most cores liefert Ergebnisse mit den folgenden Parametern.
| Datensatz | Laufzeit | Speicherverbrauch der Berechnung | Anzahl der resultierenden Kerne |
|---|---|---|---|
| Homo Sapiens | 3,798s | 41MB | 186 |
| SaccCere | 302,558s | 32MB | 4630 |
| DBLP | 95,32s | 841MB | 746 |
Größe der Ergebnisse
| Datensatz | Anzahl der resultierenden Kerne | Größe der Eingabedatei | Größe der resultierenden Datei |
|---|---|---|---|
| Homo Sapiens | 186 | 2MB | 0,065MB |
| SaccCere | 4630 | 3MB | 6,1MB |
| DBLP | 746 | 17,1MB | 0,061MB |
Die Größe der Kerne zusammengenommen ist bei dem Homo und dem DBLP Datensatz um drei, beziehungsweise vier Größenordnungen geschrumpft. Jedoch ist die Größe der Summe der resultierenden Kerne beim SaccCere Datensatz doppelt so groß, wie die Eingabe. Dies könnte durch seine besonders hohe average-degree density zu Stande kommen, weswegen die Knoten untereinander sehr stark verknüpft sind und die innersten Kerne daher sehr groß sind. Jedoch gelten auch hier die Vorteile der k-core decomposition in der weiteren Verarbeitung der Daten.
Zur Speicherung von einem dieser Kerne muss man nun lediglich den maximalen durch seine Knoten induzierten Teilgraphen berechnen, was trivial ist und hier nicht berücksichtigt wird.
5. Zusammenfassung
In diesem Paper gingen wir der Vereinfachung von Graphen zum Zweck der Verringerung ihres Speicherverbrauches, unter Berücksichtigung der Weiterverarbeitung der Daten nach. So waren die vorgestellten Methoden zur Gruppierung von Graphen besonders bei großen Graphen sinnvoll, da diese die grobe Struktur des Graphen beibehalten. Die vorgestellte Methode zur Transformation von Graphen eignete sich besonders für Machine Learning, da sie ihre Ergebnisse in Form eines Vektorraumes zurückgab, welche sich in diesem Kontext besonders gut verarbeiten lassen. Die letzte vorgestellte Methode war der Multilayer-k-core, welcher in Kombination mit einer Filterung der innermost-cores in den meisten Fällen eine effiziente und effektive Verringerung der Knoten- und Kantenzahl bewerkstelligen konnte. Die resultierenden Kerne bildeten eine gute Grundlage für die effektive Lösung weiterer Probleme, wie dem densest-subgraph oder dem community-search Problem.
Unsere Ergebnisse lassen auf die Relevanz und Sinnhaftigkeit von Speicheroptimierung schließen. Wichtig dabei ist die Berücksichtigung von Informationsverlust und das Auswählen der richtigen Methode. Oftmals sind einige Informationen eines Graphen nicht relevant, wodurch der Verlust dieser keine Probleme bereitet. Des Weiteren ist die Reduzierung des Speicheraufwandes eine bedeutende Abhilfe für die Weiterverwendung von Datensätzen.
Zukünftig wäre es wichtig, sich intensiv mit der Frage zu beschäftigen, welche Informationen benötigt werden und in welcher Form. Dabei sollte ebenfalls jederzeit das Ziel der Vereinfachung berücksichtigt werden. Die Beachtung dieser Punkte sollte es ermöglichen, eine optimale Methode für den Zweck zu finden.
6. Referenzen
- Kossinets, G. (2006). Effects of missing data in social networks. Social Networks, 28(3), 247–268.
- Laumann, E. O., Marsden, P. V., & Prensky, D. (1989). The boundary specification problem in network analysis. Research Methods in Social Network Analysis, 61(8).
- Interdonato, R., Magnani, M., Perna, D., Tagarelli, A., & Vega, D. (2020). Multilayer network simplification: approaches, models and methods. Computer Science Review, 36, 100246.
- Tian, Y., Hankins, R. A., & Patel, J. M. (2008). Efficient aggregation for graph summarization. Proceedings of the 2008 ACM SIGMOD International Conference on Management of Data, 567–580.
- Maccioni, A., & Abadi, D. J. (2016). Scalable pattern matching over compressed graphs via dedensification. Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 1755–1764.
- Grover, A., & Leskovec, J. (2016). node2vec: Scalable feature learning for networks. Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 855–864.
- Liu, B., Zhang, F., Zhang, C., Zhang, W., & Lin, X. (2020). Corecube: Core decomposition in multilayer graphs. International Conference on Web Information Systems Engineering, 694–710.
- Galimberti, E., Bonchi, F., Gullo, F., & Lanciano, T. (2020). Core decomposition in multilayer networks: Theory, algorithms, and applications. ACM Transactions on Knowledge Discovery from Data (TKDD), 14(1), 1–40.
- Xu, M. (2021). Understanding graph embedding methods and their applications. SIAM Review, 63(4), 825–853.
- Liu, W., Chen, P.-Y., Yeung, S., Suzumura, T., & Chen, L. (2017). Principled multilayer network embedding. 2017 IEEE International Conference on Data Mining Workshops (ICDMW), 134–141.
- Malliaros, F. D., & Vazirgiannis, M. (2013). To stay or not to stay: modeling engagement dynamics in social graphs. Proceedings of the 22nd ACM International Conference on Information & Knowledge Management, 469–478.
- Adamic, L. A., & Glance, N. (2005). The Political Blogosphere and the 2004 U.S. Election: Divided They Blog. Proceedings of the 3rd International Workshop on Link Discovery, 36–43. https://doi.org/10.1145/1134271.1134277
- Bonchi, F., Gionis, A., Gullo, F., Tsourakakis, C. E., & Ukkonen, A. (2015). Chromatic correlation clustering. ACM Transactions on Knowledge Discovery from Data (TKDD), 9(4), 1–24.