Adaption Multilayer-Netzwerke für traditionelle OCDA
| Arben Abazi |
|---|
| RWTH Aachen University |
| arben.abazi@rwth-aachen.de |
| Femke Pfaue |
|---|
| RWTH Aachen University |
| femke.pfaue@rwth-aachen.de |
| Sinan Lindemann |
|---|
| RWTH Aachen University |
| sinan.david.lindemann@rwth-aachen.de |
Abstract
Schon seit Jahren wächst die Relevanz und der Einfluss von sozialen Medien. Immer mehr Menschen sind auf verschiedensten Social-Media-Plattformen aktiv und produzieren dabei immense Datensätze, welche durch passende Analyse ein großes Potential mitbringen. Die hohe Anzahl der verschiedenen Informationen auf separaten Plattformen ist ein Paradebeispiel für die Anwendung von Multilayer-Netzwerken, welche die Nutzer:innendaten in verschiedenen Schichten speichern und in Relation zueinander setzen. Algorithmen speziell für die Detection von Overlapping Communities auf Multilayer-Netzwerke existieren bisher kaum, für Monolayer-Netzwerke hingegen gibt es eine breite Auswahl an verschiedenen Algorithmen. Anstatt für die Analyse dieser Netzwerke neue Algorithmen zu schreiben, kann es daher von Vorteil sein, ältere Overlapping Community Detection Algorithmen zu nutzen.
Das Transformieren von Multilayer-Netzwerken, sodass traditionelle Overlapping Community Detection Algorithmen diese verarbeiten können, ist durch die bereits bestehende große Ansammlung von effizienten Overlapping Community Detection Algorithmen ein sinnvoller Aufwand. Im Folgenden werden verschiedene Methoden untersucht, mit denen Multilayer-Netzwerke so adaptiert werden können, dass sich traditionelle Overlapping Community Detection Algorithmen darauf anwenden lassen, sowie diese mit Beispielen erläutert. Dabei werden Fehlerquellen erörtert, sowie Ansätze für spätere Interpretationen geliefert. Ebenso ist im Zuge der Automatisierung für größere oder verschiedene Datensätze der algorithmische Ansatz von zentraler Relevanz und wird dementsprechend eine Einbindung finden. Der Fokus liegt hierbei nicht in der Programmierung, sondern in einer generellen strukturellen Vorgehensweise für eine Transformierung von einem nahezu beliebigen Multilayer-Netzwerk. Diese systematische Herangehensweise wird ebenfalls an einem Beispiel vorgeführt.
Inhaltsverzeichnis
1. Einleitung
Um Multilayer-Netzwerke hinsichtlich der in ihnen vorhandenen Gruppen bzw. Communities (in diesem Paper wird der Begriff Communities verwendet) zu analysieren gibt es verschiedene Ansätze. Zum einen ist es möglich, traditionelle Overlapping Community Detection Algorithmen (OCDA) für Monolayer-Netzwerke so zu modifizieren, dass sie auf Multilayer-Netzwerken laufen können, wie in dem Artikel „Adaption traditioneller OCDA für Multilayer-Netzwerke“ besprochen, oder auch neue OCDA speziell für die Anwendung auf Multilayer-Netzwerken zu entwerfen (siehe „Neue OCDA für Multilayer-Netzwerke“.
Eine weitere Möglichkeit ist es, die Multilayer-Netzwerke so anzupassen, dass sich bereits vorhandene traditionelle OCDA auf sie anwenden lassen (Berlingerio et al., 2011), was vor Allem von Vorteil ist, da die Forschung an OCDA für Monolayer-Netzwerke deutlich weiter fortgeschritten ist als die Forschung zu Algorithmen speziell für Multilayer-Netzwerke. Dies lässt sich darauf zurückführen, dass sich die Wissenschaft mit der Thematik bereits länger befasst. Dadurch erweisen sich diese Algorithmen als stabiler, optimierter und effizienter als neu entwickelte für Multilayer-Netzwerke. Nachteilig ist jedoch, dass durch die Anpassung an für Monolayer-Netzwerke entwickelte OCDA wichtige Informationen verloren gehen, was durch die Weiterentwicklung von Methoden zur Adaption vermindert werden soll. (Huang et al., 2020), (Afsarmanesh & Magnani, 2016) Im Folgenden werden verschiedene Ansätze zur Adaption von Multilayer-Netzwerken für traditionelle OCDA vorgestellt, angewendet, verglichen und bewertet.
2. Verwandte Arbeiten
2.1 Multilayer Network Simplification
Die Vereinfachung von Mutlilayer-Netzwerken wird schon seit einigen Jahren erforscht, dementsprechend gibt es bereits gute Forschungsbeiträge zu der Thematik. Diese befassen sich jedoch mit mehr als der Reduzierung auf eine einzelne Ebene. Besonders erwähnenswert ist hier unter anderem das Werk von Interdonato (Interdonato et al., 2020), in welchem verschiedene Klassen von Vereinfachungen vorgestellt und auf verschiedene Kriterien analysiert werden. In der Arbeit kommen einige Vereinfachungsprozesse vor, die hier nicht beachtet werden müssen, da diese nicht zu einem einzelnen Layer führen.
2.2 ABACUS: Community Detection mit Frequent Closed Itemsets
Im Paper “ABACUS: frequent pAttern mining-BAsed Community discovery in mUltidimesnional networkS” führen Michele Berlingerio et al. den ABACUS-Algorithmus ein, welcher in 3.2 erläutert wird und auf der Entdeckung von Frequent Closed Itemsets basiert. Dabei werden Communities als Knoten definiert, die in den einzelnen Layern des Netzwerkes in gleichen Communities liegen, womit auch nicht direkt verbundene Knoten in der selben Community liegen können (Berlingerio et al., 2013).
Außerdem werden sowohl qualitative als auch quantitative Vergleiche mit anderen Ansätzen gezogen.
3. Methodik
Die Ansätze zur Adaption von Multilayer-Netzwerken für traditionelle OCDA lassen sich in zwei Untergruppen teilen: zum einen Flattening Methods, bei denen ein Multilayer-Netzwerk mit Hilfe von mathematischen Funktionen zu einem Monolayer-Netzwerk umgewandelt wird(Interdonato et al., 2020), auf dem dann der OCDA laufen gelassen wird, und zum Anderen Aggregation Methods, die entgegengesetzt arbeiten(Huang et al., 2020): der OCDA wird zuerst auf den einzelnen Layern, welche dann jeweils als Monolayer-Netzwerk behandelt werden, ausgeführt und danach werden die hierbei entdeckten Communities Analysiert. (Huang et al., 2020)
Dabei können je nach gewünschten Anforderungen passende OCDA gewählt werden. Die Wahl der OCDA beeinflusst das Ergebnis, es muss also abgewägen, welcher für die jeweilige Aufgabenstellung sinnvoll scheint. (Berlingerio et al., 2013), (Zhu & Li, 2014), (Berlingerio et al., 2011)
Es ist zu beachten, dass der Begriff “Aggregation Methods” sowohl Aggregation Methods als auch Flattening Methods zusammenfasst (Tagarelli et al., 2017), an dieser Stelle wird der Begriff jedoch ausschließlich in dem zuvor erklärten Kontext verwendet, da dies in der aktuellen Forschung üblich ist und das Verständnis erleichtert.
Bei der Adaption, also der Anpassung eines Multilayer-Netzwerkes kann es zu vielen Schwierigkeiten kommen. Die meisten stehen in einer engen Abhängigkeit zu der Art des Mulitlayer-Netzwerkes. Eine Unterscheidung von verschiedenen Arten ist hierbei unumgänglich. Eine erste Unterscheidung findet anhand der bestehenden Knoten statt. Haben die Layer mindestens einen gemeinsamen Knoten, so sprechen wir von einem Multiplex-Netzwerk.(De Domenico et al., 2013) Wenn alle Knoten in allen Layern vorkommen, wird dies als ein Node-aligned Multiplex-Netzwerk definiert. Die zweite wichtige Definition umfasst die Interconnected Networks, welche sich durch mehrere Layer mit mindestens einer Verbindung zwischen diesen auszeichnet. Besonders für diese beiden Arten von Netzwerken ist, dass die Layer einzeln bestehen könnten, das heißt es gibt keine zwingende Abhängigkeit zwischen den Layern. Es gibt auch weitere Arten von Netzwerken, die hier außer Acht gelassen werden, da Multiplex die häufigste Form bei sozialen Netzwerken ist und Interconnected die meisten anderen Fälle abdeckt.(Kivelä et al., 2014)
3.1 Flattening Methods
Bei den Flattening Methods werden die verschiedenen Layer eines Multilayer-Netzwerkes zu einem Monolayer-Netzwerk komprimiert (Tagarelli et al., 2017) und auf diesem dann ein beliebiger OCDA angewendet. Die Herausforderung besteht dabei darin, diese Vereinfachung mit möglichst geringem Informationsverlust durchzuführen. Im Folgenden werden verschiedene Ansätze, welche flattening umsetzen, vorgestellt.
3.1.1 Transformation durch Matrixaddition
Handelt sich um ein Node-aligned Multiplex-Netzwerk, so lässt sich das Netzwerk durch eine Matrixaddition in ein Monolayer-Netzwerk überführen. Haben wir ein Multiplex-Netzwerk gegeben, welches fast vollständig Node-aligned ist und nur fehlende Knoten in Layern besitzt, so kann man diese in den anderen Layern ohne Verbindungen ergänzen. Durch das Einbinden der Knoten ohne Verbindung in die Layer entsteht ein Node-aligned Multiplex-Netzwerk, wobei lediglich die Information über die Differenzierung, ob der Knoten keine Verbindungen oder nicht existent war, verloren geht.
Stellt man diese Layer nun jeweils als eine Adjazenz-Matrix dar, kann man diese durch eine Matrix-Addition(Interdonato et al., 2020),(Taylor et al., 2016) miteinander verknüpfen. Man erhält einen einzelnen Layer, welche alle Verbindungen enthält. In dieser Darstellung kann man nun die Wertigkeit der Verbindungen nicht mehr unterscheiden. Eine enge Freundschaft lässt sich nicht von einer flüchtigen digitalen Bekanntschaftt unterscheiden. Um dieses Problem mit relativ geringen Aufwand zu lösen, bietet es sich an gewichtete Adjazenz Matrizen(Interdonato et al., 2020) zu nutzen. Es lässt sich eine bijektive Funktion definieren, sodass mehrere Matrizen verknüpft werden und am Ende weiterhin jede Verbindung entschlüsselt werden kann.
Wir stellen nun eine eigene bijektive Additionsfunktion auf, welche die Verschlüsselungsfunktion enthält, die anhand der bekannten Binärcodierung erstellt wird.
Seien
\(A1…An,n \in \mathbb{N}\) unsere Matrizen der einzelnen Layer mit dem Ident n. Wir definieren nun eine Funktion
\(\tau:M\xrightarrow[]{} Z\), wobei Z der fertigen Matrix entspricht. Nun definieren wir die Funktionsgleichung als
\(\tau(M)= A\)1\(⋅2^0+A\)2\(⋅2^1+⋯+ An⋅2\)(n-1). Durch die Multiplikation mit Zweierpotenzen erhält jeder Eintrag in der zusammengefügten Adjazenzmatrix nun eine Dezimalzahl, die sich in eine Darstellung der Beziehungen decodieren lässt. Dafür muss die Zahl lediglich in ihre Binärform umgeschrieben werden. Aus der Darstellung in der Binärform lassen sich dann die verschiedenen Verbindungen ablesen.
Zur Verdeutlichung, liegt hier ein kleines eigenes Beispiel vor. Wir haben ein Multilayer-Netzwerk gegeben mit drei Layern. Die Layer sind in ihrer Adjazenzmatrix gegeben mit (Abbildung 1) für die Kommunikation über Instagram, (Abbildung 2) als WhatsApp Gespräche und (Abbildung 3) als reale Kontakte. Die Layer sind untereinander verbunden durch die Knotennummerierung, die für die Zuweisung von Accounts zu einer realen Person dient.
\(L_1 =\left[\begin{array}{rrr}
0&1&1&1&1\\
1&0&1&0&0&\\
1&1&0&1&1\\
1&0&1&0&0\\
1&0&1&0&0\\
\end{array} \right]\)Abbildung 1 (Layer 1, Darstellung der Kontakte auf Instagram)
\(L_2 =\left[\begin{array}{rrr}
0&1&1&0&1\\
1&0&1&0&0&\\
1&1&0&1&1\\
0&0&1&0&0\\
1&0&1&0&0\\
\end{array} \right]\)Abbildung 2 (Layer 2, Darstellung der Kontakte auf WhatsApp)
\(L_2 =\left[\begin{array}{rrr}
0&0&0&0&0\\
0&0&1&0&0&\\
0&1&0&0&0\\
0&0&0&0&0\\
0&0&0&0&0\\
\end{array} \right]\)Abbildung 3 (Layer 3, Darstellung persönlicher Kontakte)
Nach Anwendung der erweiterten Matrixaddition erhält man nun eine gewichtete Adjazenzmatrix (Abbildung 4). In dieser können wir nun alle Informationen des Multilayer-Netzwerkes vereinigt sehen. Der Eintrag 7 zwischen Knoten 2 und 3 lässt sich also Entschlüsseln zu den Informationen, dass beide Leute sich sowohl über Instagram, WhatsApp als auch in Echt unterhalten. Währenddessen bedeutet eine 3, dass die Menschen nur über Instagram und WhatsApp in Kontakt stehen. Instagram hat in dem Beispiel die Wertigkeit 1, WhatsApp die 2 und reale Kommunikation die 4. Somit lassen sich alle Informationen aus dem Ergebnis wieder ausrechnen.
\(L_2 =\left[\begin{array}{rrr}
0&3&3&1&3\\
3&0&7&0&0&\\
3&7&0&3&3\\
1&0&3&0&0\\
3&0&3&0&0\\
\end{array} \right]\)Abbildung 4 (Ergebnis der erweiterten Matrixaddition)
Dies ist zwar bei kleineren Netzwerken noch sehr übersichtlich kann bei Netzwerken mit hunderten Layern jedoch zu einem ordentlichen Aufwand werden. Es bietet sich an, Automatisierung durch Algorithmen vorzunehmen. Das Vereinfachen durch die gegebene Formel lässt sich schnell mit einer Decodierungsfunktion implementieren und läuft relativ zügig. Bei der Analyse des Netzwerkes muss allerdings die Decodierung beachtet werden und die Bedeutungen der verschiedenen Werte kann sehr unterschiedlich sein. Dies führt dazu, dass meist Algorithmen für die Analyse der individuellen Datensätze erstellt oder modifizier werden müssen und die Gefahr eines Informationsverlustes mit einhergehender Fehlinterpretationschance besteht.
Diese einfache Anpassung von Multilayer-Netzwirken birgt dementsprechend in der Analyse einen größeren Aufwand. Zudem ist sie nur für Multiplex-Netzwerke möglich, die idealerweise simple zu einem Node-aligned Multiplex-Netzwerk überführt werden können. In der realen Welt der Datensatz-Analyse von sozialen Medien kommt diese spezielle Art von Netzwerk zwar häufig vor, aber oftmals sehr unvollständig, da keine vollständige Identifizierung von zusammengehöriger Accounts möglich ist. Ausnahmen stellen hier die Analysen von den Netzwerkbetreibenden dar, da diese über einen vollständigeren Zugang zu Informationen über die Accounts und deren Verknüpfung verfügen. Häufig sind die Layer zwischen den Netzwerken nur teilweise verknüpft, das heißt, dass die Accounts nur teils Personen definitiv zugeordnet werden können. Es müsste hier also zunächst eine Ergänzung der fehlenden Knoten stattfinden oder eine erste Analyse auf Gemeinsamkeiten von Knoten.
Für andere Arten von Multilayer-Netzwerken bieten sich dann alterative Vorgehensweisen der Transformation an.
3.1.2 Flattening mit Ähnlichkeit
Eine weitere Möglichkeit, die Informationen von Graphen nach der Adaption beizubehalten, ist das Setzen von Kantengewichten, die dem Informationsverlust entgegenwirken. Ein traditionelles Netzwerk kann aufgrund seines Aufbaus die mehrdimensionalen Beziehungen eines Multilayer-Netzwerkes nicht differenziert darstellen. Aus diesem Grund einen sich Kantengewichte, um den Kanten eines Monolayer-Netzwerkes zusätzlichen Informationsgehalt zu verleihen, folglich die Communities beizubehalten. Falls zwei Knoten im Multilayer-Netzwerk in einer Community liegen, so sollen diese auch nach der Adaption in derselben Community sein. Je mehr Nachbarn sich zwei Knoten teilen, desto enger ist deren Beziehung zueinander und auch die Wahrscheinlichkeit, dass diese Knoten in derselben Community sind.
Diese Eigenschaft kann man mit der Ähnlichkeit von zwei Knoten quantifizieren.
Chen nutzt dafür den Jaccard Koeffizient(Chen et al., 2020), der die Ähnlichkeit zwischen zwei Mengen berechnet:
Dabei stellen A und B die Nachbarn von den Knoten a und b dar.
Mit der Gleichung erhalten wir einen Wert zwischen 0 und 1. Je größer der Wert, desto ähnlicher sind zwei Knoten.
Nun kann man durch das Multilayer Netzwerk laufen und für alle Knoten, die mit einer Kante verbunden sind, nach dieser Formel die Ähnlichkeit berechnen und diese als Kantengewicht setzen.
3.1.3 Unified Matrix
Eine weitere Art des flattenings bietet die Unified Matrix(Zhu & Li, 2014), die ebenfalls mit Gewichtungen versucht den Informationsverlust des flattenings abzufangen. Aus einem gegeben Multiplex-Netzwerk wird mathematische eine einzelne gewichtete Adjazenzmatrix gebildet, mit welcher sich das Netzwerk als ein Monolayer-Netzwerk darstellen lässt. Hierbei wird aus einem Multilayer-Netzwerk eine gewichtete Adjazenzmatrix erstellt, die sich als traditioneller bzw. monodimensionaler Graph mit Kantengewichten abbilden lässt (Afsarmanesh & Magnani, 2016),(Berlingerio et al., 2011), (De Domenico et al., 2013).
Korrelation
Hierbei betrachtet man zunächst die Korrelation zwischen einem Knoten und zwei Layern. Bei der Korrelation handelt es sich um eine Kenngröße, die aussagt, wie der Knoten zu den zwei Layern in Beziehung steht (mucha et al., 2010). Die Korrelation von einem Knoten i in Layer s zu einem anderen Layer r ist wie folgt durch Zhu definiert(Zhu & Li, 2014):
Der Zähler beinhaltet die Anzahl der Kanten, die Knoten i verbinden und in Layer s und Layer r existieren. Im Nenner werden wiederum alle Kanten aufgezählt, die Knoten i verbinden und in Layer s oder Layer r aufkommen, wobei eine Kante, die in beiden Layern auftritt, nur einmal gezählt wird. Die Variable \(a_{ij}^s\) wird gleich 1, falls im Layer s eine Kante zwischen Knoten i und Knoten j besteht, sonst 0.
Je größer \(C_{isr}\), desto größer ist die Interaktion von Knoten i zwischen Layer s und r. Wir erhalten also die Korrelation eines Knotens zu zwei Layern. Wenn man nun mit
die Korrelationen aufsummiert, erhält man die Korrelation von zwei Layern zueinander. N steht hier für die Anzahl der gesamten Knoten im Multilayer-Netzwerk (Zhu & Li, 2014).
Weiter leitet Zhu nun die Wichtigkeit eines Layers(Zhu & Li, 2014) unter der Betrachtung der Korrelation(Le Merrer & Trédan, 2009), wie folgt ab:
Der Zähler beinhaltet die Korrelation zwischen Layer s und r, der Nenner umfasst die Korrelationen zwischen Layer s und allen anderen Layern.
Wenn die Korrelation von einem Layer zwischen anderen Layern größer ist, dann ist auch die Wichtigkeit jenes einzelnen Layers größer.
Ähnlichkeit
Auch in diesem Algorithmus wird die Ähnlichkeit zwischen zwei Knoten herangezogen, mit analoger Begründung wie im Abschnitt Flattening. Es wird jedoch ein anderer Ansatz zur Berechnung verwendet mit der Formel
Im Gegensatz zum Jaccard Koeffizienten kann man nun auch die Ähnlichkeit von zwei Knoten berechnen, die nicht direkt durch eine Kante verbunden sind (Dang & Viennet, 2012).
Man benutzt die von Symeonidis eingeführte und von Zhu weiterentwickelte Formel zur Berechnung der Ähnlichkeit(Symeonidis et al., 2010),(Zhu & Li, 2014) zwischen zwei Knoten.
\(Sim(v_i,v_j)=\begin{cases}
1, & \text{wenn $v_i$ gleich $v_j$ ist}.\\
\sum_{B \in P} \prod_{E(u,w) \in B} S(u,w), & \text{wenn Pfade zwischen $v_i$ und $v_j$ existiert}.\\
0, & \text{sonst}.
\end{cases}\)
\(P\) sind alle Pfade zwischen Knoten \(v_i\) und \(v_j\) und E\((u,w)\) ist dabei eine Kante des Pfades \(B\).
Die Ähnlichkeiten der Knoten in Layer i werden in der quadratische Matrix \(A_{(u,w)}^i = Sim(u,w)\) gespeichert und folglich werden alle Ähnlichkeiten(Zhu & Li, 2014) der n Knoten von m Layern durch die Formel von Zhu gegeben:
Zusammensetzung aller Kenngrößen
Nach der Berechnung aller benötigten Werte erhält man die von Zhu definierte Unified Matrix(Zhu & Li, 2014):
L ist die Matrix des monodimensionalen Graphens über die Summe der m Layer. Die Einträge der Matrix enthalten in der i-ten Zeile und j-ten Spalte die Verbindung von dem i-ten und j-ten Knoten mit dem Kantengewicht in dem jeweiligen Eintrag.
Anwendung an einem Beispiel
Zur Veranschaulichung betrachten wir uns einen Multilayer-Netzwerk mit den folgenden drei Layern, die aus jeweils 4 Knoten bestehen.
 Abbildung 5 (Beispiellayer)
Abbildung 5 (Beispiellayer)
Die Layerverbindungen stehen immer zwischen den selben Knoten, der Knoten von Layer 1 ist mit dem Knoten 1 von Layer 2 verbunden et cetera.
Nach der Anwendung des Algorithmus erhalten wir die unified matrix L:
\(L =\left[\begin{array}{rrr}
1&0.28&0.24&0.15\\
0.28&1&0.34&0.09\\
0.24&0.34&1&0.21\\
0.15&0.09&0.21&1\\
\end{array} \right]\)Abbildung 6 (Unified Matrix)
Und den dazugehörigen Graphen:
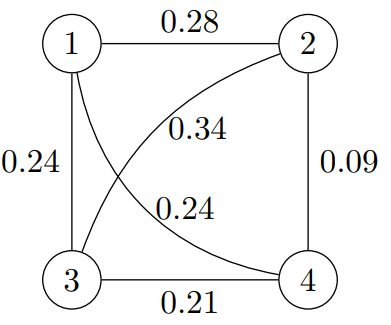
Die jeweiligen i-Spalten beinhalten die gewichteten Interaktion der i-Knoten. Je höher der Eintrag \(a_{ij}\) der Matrix, desto größer ist die Interaktion zwischen den Knoten i und Knoten j.
Vergleicht man nun die erste Spalte mit der vierten, so lässt sich erkennen, dass Knoten 1 in der Summe mehr Interaktionen mit den anderen Knoten besitzt als Knoten 4. Dies erkennt man auch bei nähere Betrachtung der einzelnen Layer, zumal der Knoten 1 den Grad 5 besitzt und Knoten 4 den Grad 2.
3.2 Aggregation Methods
Die zweite häufig genutzte Herangehensweise, um Multilayer-Netzwerke hinsichtlich ihrer Communities mit Hilfe von traditionellen OCDA zu untersuchen ist, zuerst die einzelnen Layer oder auch Dimensionen wie Monolayer-Netzwerke zu behandeln und auszuwerten, und die dabei gewonnenen Informationen im Nachhinein wieder zusammenzufügen. Diese Methoden fallen unter den Begriff Aggregation Methods.
Bei der Anwendung von Flattening Methods wird die Bedeutung des Layers, in welchem sich eine Kante befindet, also die Art der Interaktion, für gewöhnlich nicht beachtet (Berlingerio et al., 2011), was bei der Anwendung von Aggregation Methods behoben werden kann.
Der ABACUS-Algorithmus von Berlingerio et al.(2013) ist eine Kombination von verschiedenen, teilweise frei wählbaren Algorithmen. Zuerst wird ein CD-Algorithmus auf die einzelnen Layer angewendet und anschließend mit Hilfe eines Frequent Closed Itemset Mining-Paradigmas untersucht. Dabei können beliebige Community-Detection-Algorithmen verwendet werden, wobei sich dieses Paper auf OCDA bezieht. Im Folgenden wird also von OCDA gesprochen. Der Algorithmus kann u.a. auch Communities erkennen, welche aus nicht durch eine direkte Kante verbundenen Knoten bestehen(Berlingerio et al., 2013). Dies ist realitätsnah, da auch im echten Leben bzw. in sozialen Netzwerken häufig Gruppen existieren, in welchen einzelne Gruppenmitglieder nicht in direktem Kontakt zueinanderstehen, also nur im Gruppenkontext, aber nicht privat, Kontakt zueinander haben.
ABACUS
Der ABACUS-Algorithmus benötigt drei Parameter:
- Ein Multilayer-Netzwerk G
- Einen OCDA für Monodimensionale Netzwerke (hierbei kann es sich auch um einen einfachen CDA handeln)
- Eine minimale Schwelle σ (minimal support threshold)
Zuerst wird das Multilayer-Netzwerk in Monolayer-Netzwerke zerlegt, indem für jeden Layer l ein Netzwerk erstellt wird, welches sämtliche in i vorkommende Knoten und Kanten enthält. Interlayer-Kanten können dabei nicht berücksichtigt werden da davon ausgegangen wird, dass jeder Layer eine Art der Verbindung darstellt. Daraufhin wird der gewählte OCDA auf den einzelnen Netzwerken laufen gelassen, wobei für jeden Knoten n die Zugehörigkeiten zu den Communities in den verschiedenen Netzwerken (bzw. Layern) in Form von Tupeln (i,j) gespeichert wird.
Dabei stellt i die Dimension, also den Layer, und j die Communitys dar. Hierbei ist es wichtig zu beachten, dass die Wahl des OCDA maßgeblich bestimmt, welche Communities erfasst werden und ob Kantengewichte etc. einbezogen werden. Die Tupel und σ werden nun an ein frei wählbares Frequent Closed Itemset Mining-Paradigma übergeben, welches wiederkehrende Muster in j erkennt und Frequent Closed Itemsets zurückgibt, welche die gesuchten Communities darstellen.(Berlingerio et al., 2013)
Frequent Closed Itemsets werden gebildet, indem untersucht wird, welche Knoten häufig in einer gemeinsamen Community liegen (Pei et al., 2000), ein einfaches Beispiel wäre beim online Shopping der Vorschlag, was häufig gemeinsam gekauft wird: dadurch, dass die Produkte häufig zusammen gekauft werden, also eine Community bilden, werden sie in ein Cluster gespeichert und bilden ein Frequent Closed Itemset.
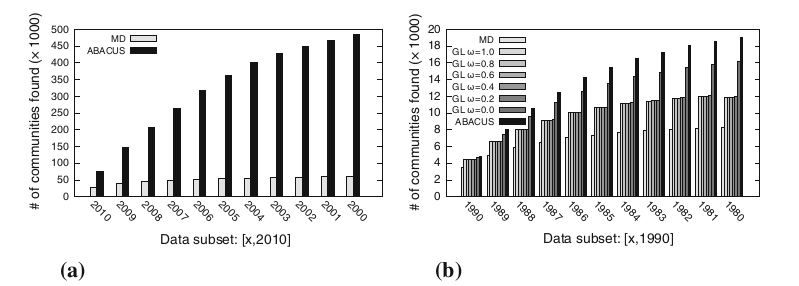
Abbildung 8: Vergleich von ABACUS, (MD) und (GL) anhand von co-Autorschaft in wissenschaftlichen Veröffentlichungen. Jedes Jahr wird durch einen Layer repräsentiert, mit jedem Jahr wächst das Netzwerk also um einen Layer.
(a) Auf große Netzwerke (>100 Dimensionen, >150 000 Knoten) kann (GL) nicht angewendet werden. Während die Anzahl an entdeckten Communities bei (MD) kaum wächst, steigt die Anzahl bei ABACUS deutlich an.
(b) Auf kleinen Netzwerken (<100 Dimensionen, <150 000 Knoten) verzeichnet (MD) den geringsten Zuwachs an Communities, bei (GL) wird die Anzahl der entdeckten Communities durch Wahl der Schwelle ω stark beeinflusst, ABACUS verzeichnet den größten Zuwachs an entdeckten Communities.(Berlingerio et al., 2013)
Berlingerio et al. Vergleichen die ABACUS-Methode mit einer zwei Jahre vorher entwickelten flattening method (MD) (Berlingerio et al., 2011) sowie einer von Mucha et al. Erforschte Methode (GL)(mucha et al., 2010), wie in Abb. 3 zu sehen. (MD) gewichtet die Kanten verschiedener Layer unterschiedlich, um möglichst viele Informationen beim Zusammenführen des Multilayer-Netzwerkes zu einem Monolayer-Netzwerk zu erhalten. Auch in diesem Verfahren kann der CD-Algorithmus beliebig gewählt werden. (Berlingerio et al., 2011) (GL) arbeitet mit dem Parameter ω, welcher das Gewicht zwischen den Layern definiert. Der Algorithmus basiert ebenfalls auf flattening. (mucha et al., 2010)
Es lässt sich nicht generalisiert sagen, ob eine der Methoden ABACUS, (MD) oder (GL) den anderen überlegen ist, auch wenn die Methoden unterschiedliche Communities liefern. Während ABACUS durch jeden weiteren Layer einen deutlichen Zuwachs an entdeckten Communities verzeichnet, ist dieser Effekt bei den anderen beiden Methoden bei mehr als vier Layern nicht mehr auszumachen. Außerdem lassen sich durch ABACUS komplexere Relationen erkennen, so lassen sich etwa Communities entdecken, die innerhalb eines Layers keine direkte Verbindung miteinander haben. (Berlingerio et al., 2013)
4. Evaluation und Kritik
In dieser Arbeit wurden verschiedene Methoden vorgestellt und erläutert, welche alle unterschiedliche Vor- und Nachteile bieten. Alle Methoden eint, dass ein gewisser Anteil an Informationen durch die Anpassung, sei es durch flattening oder aggregation, verloren geht (Huang et al., 2020), (Afsarmanesh & Magnani, 2016), (Berlingerio et al., 2013).
Sowohl bei ABACUS als auch bei der unified Matrix hat der gewählte OCDA einen sehr großen Einfluss auf die Ergebnisse (Berlingerio et al., 2013), (Interdonato et al., 2020), was zwar vorteilhaft sein kann, da die Methoden dadurch dynamisch sind und gut an die spezifischen Anforderungen angepasst werden können, allerdings die Evaluation der Performanz sowie den Vergleich mit anderen Algorithmen deutlich erschweren. Bei ABACUS kommt erschwerend hinzu, dass das Frequent Closed Itemset Mining-Paradigma ebenfalls frei wählbar ist, die Funktionsweise also noch offener definiert ist (Berlingerio et al., 2013). Dafür bietet es den Vorteil, dass auch indirekte Communities erkannt werden können. Die Anwendung der unified Matrix ist mit einem hohen Aufwand verbunden und außerdem können damit nur Ähnlichkeiten zwischen Knoten berechnet werden, welche durch eine direkte Kante verbunden sind (Interdonato et al., 2020), es können also anders als bei ABACUS keine indirekten Communities entdeckt werden. Außerdem werden die Layer gleich gewichtet (De Domenico et al., 2013), also die unterschiedliche Bedeutung nicht mit einbezogen, was zu einem Informationsverlust führt.
Die Matrixaddition hat den Kritikpunkt, dass nicht feststellbar ist, ob ein Knoten in einem Layer keine Verbindungen besitzt oder nicht existiert, des Weiteren ist die Herangehensweise für viele Layer schnell impraktikabel und garantiert ebenfalls keine Erhaltung der Informationen. Außerdem ist diese Vorgehensweise nur für Mulitplex-Netzwerke sinnvoll anwendbar.
5. Zusammenfassung
Es wurden verschiedene Methoden zur Adaption eines Multilayer-Netzwerkes für traditionelle OCDAs genannt, hierbei haben wir im Wesentlichen zwischen Flattening und Aggregation Methods unterschieden. Als Flattening Method für Node-aligned Multiplex-Netzwerke wurde zunächst die Matrixaddition mit zusätzlicher Decodierungsfunktion vorgestellt und ihre möglichen Fehlerquellen erläutert. Eine weitere Möglichkeit, Beziehungen von Knoten nach der Adaption zu wahren, liefert die Betrachtung der Knotenähnlichkeit. Hierbei wurde die Unified Matrix betrachtet, die mithilfe der Ähnlichkeit Beziehungen zwischen den Knoten beibehält. Dabei werden auch Wichtigkeiten für jeden Layer definiert, sodass sich auch Korrelationen von Layern zueinander quantifizieren lassen. Des Weiteren gibt es Aggregation Methods, von denen in diesem Paper der ABACUS-Algorithmus vorgestellt wurde. Dieser basiert auf Frequent Closed Itemsets. Das Multilayer-Netzwerk wird in Monolayer-Netzwerke aufgeteilt, ein traditioneller OCDA wird auf diesen laufen gelassen und die dadurch entdeckten Communities auf den einzelnen Monolayer-Netzwerken werden mit einem Frequent Closed Itemset Mining-Paradigma untersucht.
Dabei ist ersichtlich geworden, dass in der Informatik bereits ein Interesse an Adaptionen von Multilayer-Netzwerken besteht und dies in den nächsten Jahren zunehmen kann. Jedoch haben wir auch Bedenken, dass die Transformationsalgorithmen nicht weiterentwickelt werden, wenn die OCDAs in ihrer Kompatibilität mit Mulitlayer-Netzwerken gestärkt werden. Aus unserer Sich ist es wichtig, dass auch bei zunehmender Redundanz der Adaptionen, die Weiterentwicklung dieser nicht in Vergessenheit gerät, da sie weiterhin ihre Berechtigung im Bereich der Multilayer-Netzwerke behalten.
6. Referenzen
- Berlingerio, M., Coscia, M., & Giannotti, F. (2011). Finding redundant and complementary communities in multidimensional networks. Proceedings of the 20th ACM International Conference on Information and Knowledge Management, 2182–2184.
- Huang, X., Chen, D., Ren, T., & Wang, D. (2020). A survey of community detection methods in multilayer networks. Data Mining and Knowledge Discovery, 35(1), 1–45. https://doi.org/10.1007/s10618-020-00716-6
- Afsarmanesh, N., & Magnani, M. (2016). Finding overlapping communities in multiplex networks. ArXiv Preprint ArXiv:1602.03746.
- Interdonato, R., Magnani, M., Perna, D., Tagarelli, A., & Vega, D. (2020). Multilayer network simplification: approaches, models and methods. Computer Science Review, 36, 100246.
- Berlingerio, M., Pinelli, F., & Calabrese, F. (2013). Abacus: frequent pattern mining-based community discovery in multidimensional networks. Data Mining and Knowledge Discovery, 27(3), 294–320.
- Zhu, G., & Li, K. (2014). A unified model for community detection of multiplex networks. International Conference on Web Information Systems Engineering, 31–46.
- Berlingerio, M., Coscia, M., & Giannotti, F. (2011). Finding and characterizing communities in multidimensional networks. 2011 International Conference on Advances in Social Networks Analysis and Mining, 490–494.
- Tagarelli, A., Amelio, A., & Gullo, F. (2017). Ensemble-based community detection in multilayer networks. Data Mining and Knowledge Discovery, 31(5), 1506–1543.
- De Domenico, M., Solé-Ribalta, A., Cozzo, E., Kivelä, M., Moreno, Y., Porter, M. A., Gómez, S., & Arenas, A. (2013). Mathematical formulation of multilayer networks. Physical Review X, 3(4), 041022.
- Kivelä, M., Arenas, A., Barthelemy, M., Gleeson, J. P., Moreno, Y., & Porter, M. A. (2014). Multilayer networks. Journal of Complex Networks, 2(3), 203–271.
- Taylor, D., Shai, S., Stanley, N., & Mucha, P. J. (2016). Enhanced detectability of community structure in multilayer networks through layer aggregation. Physical Review Letters, 116(22), 228301.
- Chen, D., Du, P., Jiang, Q., Huang, X., & Wang, D. (2020). A feasible community detection algorithm for multilayer networks. Symmetry, 12(2), 223.
- mucha, P., Richardson, T., Macon, K., & Onnela, J.-P. (2010). Community structure in time-dependent, multiscale, and multiplex networks. Science, 328(5980), 876–878.
- Le Merrer, E., & Trédan, G. (2009). Centralities: capturing the fuzzy notion of importance in social graphs. Proceedings of the Second ACM EuroSys Workshop on Social Network Systems, 33–38.
- Dang, T. A., & Viennet, E. (2012). Community detection based on structural and attribute similarities. International Conference on Digital Society (Icds), 659, 7–12.
- Symeonidis, P., Tiakas, E., & Manolopoulos, Y. (2010). Transitive node similarity for link prediction in social networks with positive and negative links. Proceedings of the Fourth ACM Conference on Recommender Systems, 183–190.
- Pei, J., Han, J., & Mao, R. (2000). CLOSET: An efficient algorithm for mining frequent closed itemsets. ACM SIGMOD Workshop on Research Issues in Data Mining and Knowledge Discovery, 4(2), 21–30.