Ruizhang Zhou	Joju Mori	Tingwei Feng
RWTH Aachen	RWTH Aachen	RWTH Aachen
ruizhang.zhou@rwth-aachen.de	joju.mori@rwth-aachen.de	tingwei.fengi@rwth-aachen.de

0 Abstract

Mit der rasanten Entwicklung sozialer Netzwerke werden jede Minute und Sekunde massive soziale Daten generiert, und fast jeder hat täglich eine große Menge an Daten, die in sozialen Netzwerken generiert und ausgetauscht werden. Dies bietet uns dann eine sehr große Datenquelle, um soziale Netzwerke eingehend zu untersuchen. Wenn wir jedoch alle Inhalte miteinander mischen, erhalten wir oft chaotische und ungenaue Ergebnisse. Durch Subspace-Clustering können wir den Inhalt in mehrere Dimensionen unterteilen und mehrere Subspaces separat untersuchen, um genauere und überzeugendere Ergebnisse zu erzielen. Das Subspace-Clustering ist eine Erweiterung des herkömmlichen Clustering, bei dem versucht wird, die Clusters in verschiedenen Subspaces innerhalb eines Datasets zu finden. In hochdimensionalen Daten sind viele Dimensionen häufig irrelevant und können vorhandene Clusters in verrauschten Daten verdecken. Durch die entsprechende Funktion werden irrelevante Dimensionen entfernt, indem der gesamte Datensatz analysiert wird. Die Subspace-Clustering-Algorithmen lokalisieren die Suche nach relevanten Dimensionen, sodass sie die Clusters finden können, die in mehreren, möglicherweise überlappenden Unterräumen vorhanden sind.

1.Einleitung

Subspace-Clustering ist eine Erweiterung des Clustering, um Cluster in verschiedenen Subspaces innerhalb eines Datasets zu finden. Die Objekte werden als Messvektor oder als Punkt im mehrdimensionalen Raum dargestellt. Anhand des modernen Technik wird Daten einfacher und schneller gesammelt. Aber es fühlt zu größere und komplizierte Datasets, die mit viele Objekte und Dimensionen sind. Um Datasets besser zu organisieren , muss vorhandener Algorithmus verbessert werden. Traditionales Clustering Algorithmen berücksichtigen alle Dimensionen der Eingaben, um möglich viel Objekt zu lernen. Viele Dimensionen, die in hochdimensionalen Daten sind, sind oft irrelevant. Diese irrelevante Dimensionen können Clustering Algorithmen verwirren. Es fühlt zu Noise Data. In höher Dimensionen ist es normal, dass alle Objekte in einem Dataset nahezu gleich weit voneinander entfernt sind. Methoden zur Merkmalsauswahl werden erfolgreich eingesetzt, um die Qualität des Cluster zu verbessern. Diese Algorithmen finden eine Teilmenge von Dimensionen, um die Clustering durchführen zu können. Indem werden nicht relevante und redundante Dimensionen entfernt. Feature-Auswahlmethoden, die das Dataset als Ganzes untersuchen, lokalisieren Subraum-Clustering-Algorithmen ihre Suche und können Cluster aufdecken, die in mehreren, möglicherweise überlappenden Subspaces vorhanden sind.

Der Clustering-Algorithmus ist eine der Schlüsseltechnologien in den Bereichen künstliche Intelligenz und Data Mining und hat eine breite Palette von Anwendungen. Mit dem Aufkommen der Ära der Big Data werden viele inkonsistente Daten, gemischte Daten und Daten mit fehlenden Werten generiert. Typische Clustering-Algorithmen haben Schwierigkeiten beim Clustering dieser Datensätze. Beispielsweise existieren in hochdimensionalen, spärlichen Daten Cluster nur in einem Unterraum, der aus Teilattributen besteht. Aus der Perspektive des volldimensionalen Raums gibt es in diesen Datensätzen keine Cluster. Im Allgemeinen werden die Unterschiede zwischen Stichproben häufig durch mehrere Schlüsselmerkmale verursacht. Wenn diese wichtigen Merkmale richtig gefunden werden können, spielt dies eine positive Rolle bei der Erstellung eines angemessenen Clustering- oder Klassifizierungsmodells. Daher wird ein Subraum-Clustering vorgeschlagen.

2. Verwandte Arbeiten

Nach den aktuellen Forschungsergebnissen kann das Subraum-Clustering in zwei Formen unterteilt werden: das harte Subraum-Clustering und das weiche Subraum-Clustering. Was ist der Unterschied zwischen den beiden, unten erläutert Der Hard Subspace Clustering-Algorithmus kann den genauen Unterraum identifizieren, in dem sich verschiedene Klassen befinden. Im Gegensatz zum Hard Subspace Clustering muss beim Soft Subspace Clustering nicht der genaue Unterraum für jede Klasse gefunden werden, sondern es wird stattdessen jede Klasse angegeben Features erhalten unterschiedliche Gewichte, und diese Gewichte werden verwendet, um den Beitrag jedes Dimensions-Features in verschiedenen Klassen zu messen. Das heißt, beim Clustering von weichen Unterräumen wird für jede Klasse ein weicher Unterraum gefunden. Einfach ausgedrückt, beim Hard-Subspace-Clustering darf ein Attribut nur zu einem Subspace gehören, das Clustering wird in diesen Subspaces durchgeführt und das Gewicht des Attributs in jedem Subspace beträgt entweder 0 oder 1. Soft-Subraum-Clustering dient zum Clustering des gesamten Datensatzes in einem volldimensionalen Raum. Jeder Unterraum enthält alle Attribute, aber jedes Attribut erhält eine andere Gewichtung \([0,1]\). Die Attributgewichtung beschreibt das Attribut und den entsprechenden Unterraum. Je größer der Grad der Korrelation zwischen ihnen ist, desto größer ist das Gewicht, desto wichtiger ist das Attribut in diesem Unterraum und desto stärker ist die Korrelation mit dem Unterraum. Insbesondere können gemäß den verschiedenen Suchmethoden Hard-Subspace-Clustering-Methoden in Bottom-Up-Subspace-Suchalgorithmen und Top-Down-Subspace-Suchalgorithmen unterteilt werden; für Soft-Subspace-Clustering-Methoden Entsprechend den verschiedenen Arten, die Unsicherheit von Merkmalsgewichtungskoeffizienten auszudrücken, kann sie in Fuzzy-gewichtetes Soft-Subspace-Clustering und Entropie-gewichtetes Soft-Subspace-Clustering unterteilt werden.

3. Funktionsweise

Lassen Sie uns den Bottom-Up-Subraum-Clustering-Algorithmus in den harten Subraum-Clustering einführen. Bottom-up-Subraum-Clustering-Algorithmen basieren im Allgemeinen auf der Gitterdichte und verwenden eine Bottom-up-Suchstrategie für Subraum-Clustering-Algorithmen. Es unterteilt zuerst den ursprünglichen Merkmalsraum in mehrere Gitter und drückt dann die Dichte des Unterraums mit der Wahrscheinlichkeit aus, auf einen Abtastpunkt in einem Gitter zu fallen. Die Teilräume, deren Dichte einen bestimmten Schwellenwert überschreitet, werden als dichte Einheiten reserviert, während die nicht dichten Teilräume verworfen werden. Die klassische Bottom-Up-Subraum-Clustering-Methode verfügt über den frühesten statischen Grid-Clustering-Algorithmus CLIQUE. Der CLIQUE-Algorithmus verwendet eine Methode, die auf Gitter und Dichte basiert. Teilen Sie zuerst jedes Attribut gleichmäßig auf, und der gesamte Datenraum wird in eine Superquadermenge aufgeteilt. Zählen Sie die Datenpunkte jeder Einheit. Einheiten, die einen bestimmten Schwellenwert überschreiten, werden als dichte Einheiten bezeichnet, und verbinden Sie dann die dichten Einheiten, um eine Klasse zu bilden. Der Algorithmus ist wie folgt:

Clique Algorithmus 1: Finden Sie alle dichten Bereiche im eindimensionalen Raum, die jedem Attribut entsprechen. Dies ist eine dichte Menge eindimensionaler Zellen. 2: \(k <- 2\). 3: wiederholen 4: Es gibt alle Kandidaten für dichte \(k\)-dimensionale Einheiten, die durch dichte \(k-1\)-dimensionale Einheiten erzeugt werden. 5: Löschen Sie Einheiten mit weniger als einer bestimmten Anzahl von Punkten. 6: \(k <- k + 1\). 7: Bis es keinen Kandidaten für eine dichte \(k\)-dimensionale Einheit gibt. 8: Indem alle benachbarten Zellen mit hoher Dichte genommen und Cluster entdeckt werden. 9: Fassen Sie jeden Cluster mit einer kleinen Gruppe von Ungleichungen zusammen, die den Attributbereich der Elemente im Cluster beschreiben.

4. Anwendung

Die Schritte des CLIQUE-Algorithmus sind in die folgenden drei Teile unterteilt: 1) Identifizieren Sie den Unterraum, der Cluster enthält. 2) Identifizieren Sie diese Cluster; 3) Generieren Sie eine “minimale Beschreibung” dieser Cluster. Unter diesen bedeutet die minimale Beschreibung (minimale Beschreibung), dass diese Cluster wiederholt keine dichten Gitterzellen enthalten. Das Folgende wird separat eingeführt.

1. Identifizieren Sie den Unterraum, der Cluster enthält Die Schwierigkeit beim Identifizieren von Teilräumen, die Cluster enthalten, besteht darin, wie dichte Gitterzellen im Unterraum gefunden werden. Die einfachste Methode besteht darin, das Histogramm der Abtastpunkte in allen Unterräumen basierend auf der Anzahl der Abtastpunkte zu zeichnen, die in jeder Gitterzelle im Unterraum enthalten sind. Zeichnen Sie und beurteilen Sie dann anhand dieser Histogramme. Offensichtlich ist diese Methode nicht für hochdimensionale Datensätze geeignet, da die Anzahl der Teilräume mit zunehmender Dimension exponentiell zunimmt. In diesem Artikel führte Rakesh Agrawal eine andere “Bottom-up” (Bottom-up) -Identifizierungsmethode ein. Die theoretische Grundlage dieser Methode ist das monotone Prinzip der Clusterbewertung. Monotonieprinzip der Clusterbewertung: Wenn eine Abtastpunktmenge (Cluster) \(S\) ein Cluster im \(k\)-dimensionalen Raum ist, dann ist \(S\) Teil eines Clusters in einem beliebigen \(k-1\)-dimensionalen Unterraum des Raums. Der Beweis lautet wie folgt: Angenommen, \(S\) ist ein Cluster im \(k\)-dimensionalen Raum. Nach dem Prinzip der Gitterclusterung besteht dieser Cluster aus mehreren dichten und benachbarten Gitterzellen in einem entsprechenden Gitter in einem beliebigen Unterraum. Alle diese Punkte müssen vorhanden sein, damit das Gitter dieses Unterraums ebenfalls dicht ist, und die Nähe dieser dichten Gitter in \(S\) wird auch im Unterraum beibehalten. Dieser Algorithmus ist “Schritt für Schritt”. Er durchläuft zuerst den ursprünglichen Datensatz einmal, um eine eindimensionale dichte Gittereinheit zu erhalten. Wenn eine dichte Gittereinheit mit einer \(k-1\)-Dimension erhalten wird, kann dies durch die folgende Abbildung gezeigt werden (Abbildung 5). So generieren Sie Kandidaten-\(k\)-dimensionale dichte Gitterzellen: Nachdem Sie die Kandidaten-\(k\)-dimensionalen dichten Gitterzellen erhalten haben, durchlaufen Sie den Datensatz erneut, um die wahren \(k\)-dimensionalen dichten Gitterzellen zu bestimmen. Wiederholen Sie die obigen Vorgänge, bis keine Kandidaten-Dichtezellen mehr generiert werden bis um.

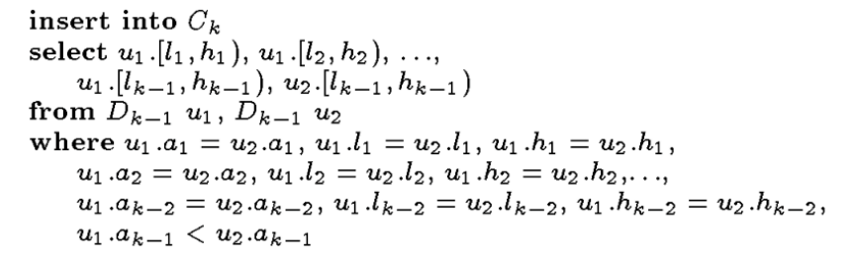
Abbildung 1 Pseudocode für den Kandidatengenerierungsschritt

Die in der obigen Abbildung gezeigten Schritte nehmen alle Sätze von \(k-1\)-dimensionalen dichten Gittereinheiten \(D­­k-1\) als Parameter und erhalten schließlich eine Obermenge \(Ck\), die alle Sätze von \(k\)-dimensionalen dichten Gittereinheiten enthält, wobei \(ui\) die \(i\)-te Dichte darstellt Für Gitterzellen mit \(k-1\)-Dimension repräsentiert \(ui.aj\) die \(j\)-te Dimension von \(ui\), und \(ui.hj\) und \(ui.lj\) repräsentieren die oberen und unteren Grenzen der \(j\)-ten Dimension des Gitters, in dem sich \(ui\) befindet. Der Pseudocode, in dem zwei ähnliche dichte Gittereinheiten mit \(k-1\)-Dimension gefiltert werden, ist in \(k-2\)-Dimensionen gleich, und dann werden sie zu einer dichten dichten Gittereinheit mit \(k\)-Dimension kombiniert, hier wir Es ist ersichtlich, dass in der letzten Zeile der Filterbedingung \(u1.ak-1\) <u2.ak-1 anstelle von u1.ak-1 ≠ u2.ak-1verwendet wird, um keine doppelten Kandidaten für dichte Gitterzellen zu erzeugen. Darüber hinaus beruht der Dimensionsvergleich hier auf einem geordneten Vergleich von Indizes und nicht auf einem Kreuzvergleich. Die obigen Schritte ähneln dem Verfahren zum Erzeugen von häufigen Objektmengen von Kandidaten durch den Apriori-Algorithmus. Bevor der Datensatz erneut durchlaufen wird, um die wahre dichte Einheit in \(C­k\) zu finden, zeigt das Monotonieprinzip der Clusterbewertung, dass nach Erhalt eines Satzes dichter \(k\)-dimensionaler Gittereinheiten Nach der Obermenge von \(Ck\) müssen wir zuerst die \(k\)-dimensionalen Gitterzellen löschen, die in keinem Unterraum der \(k-1\)-Dimension dicht sind, und dann den Datensatz durchlaufen. Diese Methode zur Verwendung von Einschränkungen des Vorwissens zur Eingrenzung des Suchraums ähnelt der Methode zum Auffinden häufiger Objektmengen im Apriori-Algorithmus. Sie weist die Eigenschaften der Skalierbarkeit auf und ihre zeitliche Komplexität beträgt \(O (c­k + mk\)), \(c\) ist eine Konstante, \(k\) ist die größte Dimension aller dichten Einheiten, \(m\) ist die Anzahl der Abtastpunkte im Datensatz und die Anzahl der Durchquerungen des Datensatzes kann mit bestimmten Mitteln verringert werden. Ähnlich wie beim allgemeinen dichtebasierten Clustering-Verfahren erzeugt der Unterraum mit der niedrigeren Dimension dichtere Einheiten, wenn der Schwellenwert \(τ\) für die Beurteilung, ob das Gitter dicht ist oder nicht, zu klein eingestellt wird, da diese als enthaltend falsch interpretiert werden Mit zunehmender Anzahl von Cluster-Teilräumen wächst der Suchraum exponentiell. Um dieses Problem zu lösen, wird auch ein verbessertes Verfahren vorgeschlagen, das auf dem Prinzip der “minimalen Beschreibungslänge” (MDL) basiert. Dieses Verfahren reduziert den Suchraum erheblich, indem es sich nur auf diese “interessanten” Teilräume konzentriert.

1. Identifizieren Sie Cluster, die von dichten Einheiten erzeugt werden Das Verfahren der Clustererkennung ist hier dasselbe wie das gitterbasierte Clustering, bei dem benachbarte dichte Gitterzellen zu einem Cluster kombiniert werden. Insbesondere wird basierend auf dem “Tiefen-zuerst-Prinzip” zuerst \(Ck\) (Pseudocode) aus \(k\)-dimensionalen dichten Zellen gesetzt Verwenden Sie \(u\), um eine dichte Gitterzelle zufällig darzustellen, und initialisieren Sie sie separat als Cluster. Durchqueren Sie dann Ck, um die dichte Zelle neben der Zelle in diesen Cluster zu unterteilen, falls noch keine vorhanden ist Wählen Sie für die geteilten Einheiten zufällig eine dieser Einheiten als neuen Cluster aus und wiederholen Sie den vorherigen Schritt, bis alle Einheiten ihre eigene Cluster-Mitgliedschaft haben. Die zeitliche Komplexität des Algorithmus beträgt \(O(2nk)\), \(n\) ist die Größe von \(Ck\). Wenn Sie eine Datenstruktur wie einen Hash-Baum verwenden, erhalten Sie eine schnellere Suchgeschwindigkeit. Der Pseudocode ist in der folgenden Abbildung dargestellt.

Abbildung 2 Pseudocode zur Identifizierung von Clustern

1. Generieren Sie die “Mindestbeschreibung” des Clusters Dieser Teil ist der Kern des Volltextes. Er bestimmt die Interpretierbarkeit des resultierenden Clustering-Modells. Dieser Prozess behandelt nicht mehrere sich gegenseitig ausschließende Cluster (Sätze dichter Gitterzellen) in einem \(k\)-dimensionalen Unterraum \(S\) als Die Eingabe und Ausgabe sind die “minimale Beschreibung” des Clusters. Diese “minimale Beschreibung” ist eine Menge \(R\) von Regionen, wobei jede Region \(r ∈ R\) in der dichten Gitterzellenmenge \(Ck\) und jeder der \(Ck\) enthalten ist Jede dichte Einheit muss zu mindestens einer dieser Regionen gehören, was offensichtlich ein \(NP\)-hartes Problem ist. Die von Rakesh Agrawal in diesem Artikel angegebene Methode ist in zwei Schritte unterteilt: 1) Verwenden Sie den “Algorithmus für gieriges Wachstum”, um den größten Bereich für jeden Cluster zu erhalten. 2) Durch Verwerfen der Gitterzellen, die wiederholt abgedeckt werden, um die “minimale Beschreibung” zu erhalten. Die beiden Schritte werden nachstehend ausführlich beschrieben. A) Holen Sie sich den größten Bereich für jeden Cluster In diesem Schritt verwenden wir eine dichte Einheit im Cluster als Anfangsregion und erweitern dann die Region basierend auf ihren (links und rechts) benachbarten Einheiten in einer bestimmten Dimension. Nach Abschluss der Erweiterung in einer anderen Dimension Basierend auf den benachbarten Einheiten aller dichten Einheiten in dem Gebiet wird das Gebiet weiter erweitert. Wiederholen Sie die obigen Schritte, bis alle k-Dimensionen durchlaufen sind, und wiederholen Sie dann den Vorgang für die Einheiten im Cluster, die nicht in dem entsprechenden Gebiet enthalten sind, bis es keine gibt In Bezug auf isolierte Gitterzellen ist zu beachten, dass die durch die obige Operation gebildete Fläche ein räumliches lineares Polygon ist. Nehmen wir zur Veranschaulichung ein Beispiel eines zweidimensionalen Raums (wie in Abbildung 3 gezeigt), wobei angenommen wird, dass \(f1\) und \(f2\) die beiden Dimensionen des Unterraums sind und Grau die dichte Einheit darstellt, wobei die dichte Einheit \(u\) der erste Bereich ist, den wir zuerst wählen Erweitern Sie \(u\) in der Dimension \(f1\), um den Bereich \(A\) zu erhalten, und erweitern Sie dann basierend auf jeder Zelle im Bereich \(A\) den Bereich in der Dimension \(f2\) weiter, um den Bereich \(B\) zu erhalten. Nachdem Sie die obigen Schritte ausgeführt haben, können Sie feststellen, dass die Zelle \(w\) nicht in dem Bereich enthalten ist, und Sie können den obigen Vorgang für \(w\) zu diesem Zeitpunkt wiederholen.

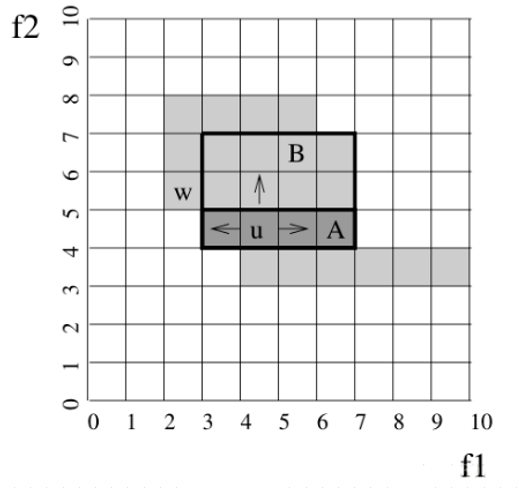
Abbildung 3 Beispiele für Algorithmen für gieriges Wachstum Es kann bewiesen werden, dass im schlimmsten Fall die zeitliche Komplexität des Algorithmus \(O(n­2(k-1)/k)\) ist, wobei \(n\) die Anzahl der im Cluster enthaltenen dichten Einheiten ist und \(k\) die Dimension des Unterraums ist, in dem sich der Cluster befindet Hier bezieht sich der “schlimmste Fall” für \(n\) dichte Einheiten, dass der benachbarte Bereich, der durch diese Einheiten gebildet wird, \(O(n(k-1)/k)\) “Ecken” enthält. Hier ist ein Beispiel eines zweidimensionalen Raums ( Wie in Abbildung 4) gezeigt, ist ersichtlich, dass die zeitliche Komplexität des Algorithmus in diesem Raum \(O (n)\) ist.

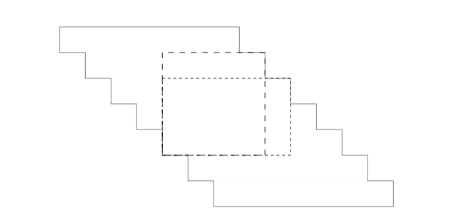
Abbildung 4 Worst-Case-Analyse im zweidimensionalen Raum Der schlechteste Fall für den Algorithmus für gieriges Wachstum (zweidimensionaler Fall): Nehmen Sie n dichte Einheiten und n1/2 obere Ecken an. Eine minimale Abdeckung muss mindestens ein Rechteck pro oberer Ecke enthalten. Da jedes Rechteck maximal ist, muss es auch die untere Treppe erreichen. Dies bedeutet, dass der Umfang des Rechtecks in \(2n1/2 + 2\) und damit seine Fläche mindestens \(n1 / 2\) beträgt. Die Summe der Größen der Rechtecke ist dann \(O (n2（2-1）/2)\).

b) die “minimale Beschreibung” erhalten Es wird empfohlen, in diesem Artikel eine heuristische Methode zum Entfernen redundanter Einheiten zu verwenden. Suchen Sie insbesondere zuerst die kleinste (die kleinste Anzahl dichter Einheiten eingeschlossen) die größte Region, wenn sich jede Einheit in dieser größten Region in anderen Regionen befindet Nach der Wiederholung wird der Bereich aus dem größten Bereich des Clusters entfernt, bis der nächste ähnliche Bereich nicht gefunden wird. Die zeitliche Komplexität des Algorithmus beträgt \(O (n2)\). Da jede Region des Clusters durch eine Reihe von Ungleichungen basierend auf Unterraumdimensionen dargestellt werden kann, wird der gesamte Cluster letztendlich durch diese Ungleichungen beschrieben.

5. Zusammenfassung und Ausblick

Der Subraum-Clustering-Algorithmus bezieht sich auf die Aufteilung des ursprünglichen Merkmalsraums der Daten in verschiedene Merkmals-Teilmengen, die Untersuchung der Bedeutung jedes Datenclusters aus verschiedenen Subraum-Perspektiven und das Auffinden jedes Datenclusters während des Clustering-Prozesses. Der entsprechende Feature-Unterraum. Im Allgemeinen gibt es zwei Hauptaufgaben beim Clustering von Unterräumen: 1) Suchen von Teilräumen (Attribut-Teilmengen), die gruppiert werden können; 2) Clustering in entsprechenden Teilräumen. Der Subraum-Clustering-Algorithmus ist tatsächlich eine Kombination aus herkömmlichen Merkmalsauswahltechniken und Clustering-Algorithmen. Beim Clustering von Datenproben werden die Merkmalsuntermengen oder Merkmalsgewichte erhalten, die jedem Datencluster entsprechen.

Der Clique-Algorithmus ist ein gitterbasierter räumlicher Clustering-Algorithmus, aber auch eine sehr gute Kombination von dichtebasierten Clustering-Algorithmen, sodass nicht nur Cluster beliebiger Formen gefunden werden können, sondern auch größere Cluster wie gitterbasierte Algorithmen verarbeitet werden können. Mehrdimensionale Daten. Der Clique-Algorithmus unterteilt jede Dimension in nicht überlappende Communitys, wodurch der gesamte Einbettungsraum von Datenobjekten in Einheiten unterteilt wird. Er verwendet einen Dichteschwellenwert, um dichte Einheiten zu identifizieren. Eine Einheit ist dicht, wenn das ihr zugeordnete Objekt den Dichteschwellenwert überschreitet . Zusammenfassung ist: Der Clique-Algorithmus ist ein gitterbasierter Clustering-Algorithmus, mit dem dichtebasierte Cluster im Unterraum gefunden werden.

Vorteil: Angesichts der Aufteilung jedes Attributs kann ein Single-Pass-Datenscan die Rastereinheiten und Rastereinheitenzahlen für jedes Objekt bestimmen. Obwohl die Anzahl potenzieller Gitterzellen hoch sein kann, muss nur ein Gitter für nicht leere Zellen erstellt werden. Ordnen Sie jedes Objekt einer Zelle zu und berechnen Sie die zeitliche und räumliche Komplexität der Dichte jeder Zelle als \(O(n)\). Der gesamte Clustering-Prozess ist sehr effizient. Der CLIQUE-Algorithmus kann automatisch den höchstdimensionalen Unterraum erkennen. CLIQUE reagiert nicht auf die Eingabereihenfolge von Tupeln, und es muss keine Standarddatenverteilung angenommen werden. Der Algorithmus skaliert linear mit der Größe der Eingabedaten. Wenn die Datendimension zunimmt, ist sie gut skalierbar. Nachteile: Wie die meisten dichtebasierten Clustering-Algorithmen hängt das gitterbasierte Clustering stark von der Wahl der Dichteschwellen ab. (Zu hoch, Cluster können verloren gehen. Zu niedrig, Cluster, die getrennt werden sollen, können zusammengeführt werden. Wenn Cluster und Rauschen unterschiedlicher Dichte vorhanden sind, können möglicherweise keine Werte gefunden werden, die für alle Teile des Datenraums geeignet sind. Mit zunehmender Dimension nimmt die Anzahl der Gitterzellen schnell zu (exponentielles Wachstum). Das heißt, für hochdimensionale Daten hat gitterbasiertes Clustering tendenziell einen schlechten Effekt. Der Clique-Algorithmus wendet eine Bereinigungstechnik an, um die Anzahl der Kandidatensätze für dichte Einheiten zu verringern, kann jedoch eine gewisse Dichte verlieren. Wenn eine Dichte im k-dimensionalen Raum existiert, ist ihre gesamte Unterraumabbildung dicht. Im Bottom-up-Algorithmus sollten alle Teilräume berücksichtigt werden, um eine k-dimensionale Dichte zu finden. Wenn sich diese Teilräume jedoch im ausgeschnittenen Raum befinden, kann die Dichte niemals gefunden werden. Da viele Schritte im Algorithmus stark vereinfacht werden und viele Schritte ungefähre Algorithmen verwenden, kann die Genauigkeit der Clustering-Ergebnisse verringert werden.

6. Referenzen