Soziale Netzwerke - Identifikation von Experten

Daria Shvakova	Lisa Wanko
RWTH Aachen University	RWTH Aachen University
daria.shvakova@rwth-aachen.de	lisa.wanko@rwth-aachen.de

Abstract

Zahlreiche Online-Gemeinschaften, vor allem Frage- und Antwort-Foren basieren auf dem Informationsaustausch zwischen Wissenssuchenden und Experten. Deshalb ist die korrekte Identifikation und Verifikation von Experten entscheidend für den Erfolg solcher Communities. Für diesen Artikel betrachteten wir die derzeit am häufigsten verwendeten Algorithmen zur Expertenfindung und Link Analysis - PageRank, Hyperlink-Induced Topic Search (HITS) - mit dem Fazit dass diese noch bestimmte Einschränkungen haben, weil sie zum Teil Probleme aufweisen wie das Ignorieren des Ausmaßes der Interaktion zwischen Nutzern (PageRank, HITS, InDegree), oder der Schwierigkeit festzulegen, wie viele Nutzer als Experten eingestuft werden sollen (PageRank, HITS).

Zur Lösung dieser Schwächen werden Overlapping Community Detection (OCD) Algorithmen in Betracht gezogen. Diese füllen erfolgreich Lücken in der Aussagekraft der Link Analysis Algorithmen und sorgen deshalb insgesamt für verbesserte Expertenerkennung. Die OCD Algorithmen teilen die Nutzer nach Gemeinsamkeiten in Communities ein. Dadurch wird es leichter Experten für einzelne Themenfelder zu identifizieren. Die Interaktionen innerhalb der jeweiligen Community können also als relevanter angesehen werden. Dass Nutzer sich in mehreren Communities befinden können, kann durch einen Faktor berücksichtigt werden. Das Finden von Experten wird also durch die Kombination der Algorithmen zur Expertenfindung mit OCD Algorithmen viel genauer und zuverlässiger.

Inhaltsverzeichnis

1. Einleitung und Erklärung
   - Verwandte Arbeiten
   
2. Methodik
   
3. Analyse
   - Evaluierung
   - PageRank
   - HITS
   - InDegree
   - Disassortative Degree Mixing and Information Diffusion (DMID)
   - Speaker Listener label Propagation Algorithm (SLPA)
   - Resultat
   - Diskussion
   - Schwächen unserer Methoden
   - Wo besteht noch Forschungsbedarf?
   
4. Schlussfolgerung (Conclusion)
5. Referenzen

Einleitung und Erklärung

Man nehme an, ein erfolgreicher Videospiel-Streamer stellt einen Weltrekord für das schnellste beenden eines bestimmten Spiels auf. Es liegt in der Natur des Spiels, dass das sehr viel Glück erfordert – und das Glück des Spielers ist außergewöhnlich gut. Zuschauer fangen an ihn zu hinterfragen wie wahrscheinlich sowas sein kann, aber Mathematik ist schwer, und nicht jeder kennt sich mit der komplizierten statistischen Auswertung von Computerprogrammen aus. Der Spieler erlässt eine öffentliche Erklärung und unterstreicht die Wahrscheinlichkeit seines Glücks mit den Berechnungen eines anonymen „Experten“.

Als Antwort meldet sich ein anderer anonymer Experte auf einer sozialen Plattform und widerspricht dem ersten – er widerlegt scheinbar seine Methoden und Schlussfolgerung, jedoch ist dies für Laien nicht nachvollziehbar. Auch von ihm kennt man weder den Klarnamen noch Kredenzen – aber man weiß, dass er oft in einer Community von Statistikern aktiv ist, viele Fragen zu genau dem Thema beantwortet und selbst sehr spezifische und schwierige Fragen stellt. Vom ersten Experten sind keine solchen Interaktionen bekannt.

Die Frage nun ist – welchem Experten schenkt man seinen Glauben? Natürlich wäre das Verfahren eines Peer-Reviews in diesem Falle am glaubwürdigsten, aber wenn man auch nicht prüfen kann ob die Peers qualifiziert sind, stellt sich nicht schnell die wissenschaftliche Methode in den Hintergrund und es wird zu einem Beliebtheits-Wettbewerb? Und was, wenn die Entscheidung schnell getroffen werden muss?

Im vorherigen Szenario ist es klar, dass eine rationale Person den zweiten Experten eher vertrauen würde, weil er durch positive Interaktionen mit einer Community von anderen Experten und Wissenssuchenden seinen Wissensstand unterstützt, während für den ersten Experten keine Interaktionen bekannt sind. Im echten Leben ist es aber oft so, dass beide gewisse Grade an Interaktionen vorweisen können – wem glaubt man dann? Der Person mit mehr Interaktion? Was wenn diese schlechte Qualität hat? Die Antworten könnten undurchdacht und oberflächlich sein, auch wenn es sehr viele sind. Der Person mit der besseren Qualität? Bei ihr kann man weder Konsistenz gewährleisten noch auf Wissen in naheliegenden aber nicht exakt gleichen Gebieten schließen.

An genau dieser Stelle kann man Algorithmen anwenden, die durch den Interaktionsverlauf einer Person darauf schließen können, ob die Person als „Experte“ in etwas eingestuft werden kann. Dabei gibt es Variationen in sowohl Methodik als auch Effektivität.

In diesem Paper vergleichen und diskutieren wir diese Algorithmen zur Expertenfindung, um zum Schluss eine Empfehlung treffen zu können, welche sich für bestimmte Rahmenbedingungen am besten eignen.

Verwandte Arbeiten

Es gibt in den Papern zu diesem Thema verschiedene Ansätze hinsichtlich der gewählten Algorithmen. Die Paper (Bouguessa et al., 2008) und (Shahriari et al., 2015) verwenden zur Gewichtung und Bewertung der Knoten innerhalb eines Netzwerkes die Algorithmen PageRank und HITS. In Paper (Bouguessa et al., 2008) werden zudem noch die Algorithmen z-Score und InDegree beschrieben und alle untereinander verglichen. In (Bouguessa et al., 2008) wurden die Algorithmen auf Frage- und Antwort-Foren zu verschiedenen Themen von Yahoo! Answers angewendet. Das Ergebnis dabei war, dass InDegree am besten zur Identifikation von Experten in eben genannten Frage- und Antwort-Foren geeignet ist.

In (Shahriari et al., 2015) werden neben den oben genannten Algorithmen noch die zwei OCD Algorithmen DMID und SLPA beschrieben. Die genannten Algorithmen wurden in (Shahriari et al., 2015) zur Expertenfindung auf Daten von drei Foren angewendet, zwei davon von stackexchange und das andere ein estnisches Natur Forum. Bei dem Vergleich der Ergebnisse der verschiedenen Algorithmen war das Fazit, dass OCD Algorithmen besser geeignet sind, da sie mehr Informationen des Graphs darin verwertet werden und daher genauere Ergebnisse erzielt werden können.

Methodik

Wir werden in diesem Paper die drei genannten Algorithmen PageRank, HITS und InDegree beschreiben und auf Beispiel Datensätze von Yahoo! Answers und anderen Foren anwenden um die erzielten Ergebnisse vergleichen zu können.

Dann werden wir die zwei OCD Algorithmen „Disassortative Degree Mixing and Information Diffusion” (Abk. DMID) und “Speaker Listener Label Propagation Algorithm” (Abk. SLPA) einführen.

Wenn die verschiedenen Algorithmen dann erklärt sind, wird der InDegree als der beste nicht-OCD Algorithmus mit den zwei OCD Algorithmen verglichen, um herauszufinden wodurch die besten Ergebnisse bei der Expertenfindung in Frage- und Antwort-Foren erzielt werden können.

Analyse

Evaluierung

Die drei im Folgenden beschriebenen Algorithmen bekommen als Eingabe ein Netzwerk von Nutzern und geben für jeden Nutzer einen Rang aus. Dann muss noch entschieden werden, ab welchem Rang ein Nutzer als Experte gilt.

PageRank

Bei dem PageRank Algorithmus teilt jeder Nutzer seinen PageRank gleichmäßig auf alle Nutzer auf, die ihm antworten konnten und verlinkt somit auf sie. Diese Beziehungen untereinander werden im Prinzip in einer Matrix dargestellt. Diese Matrix wird mit einem Vektor multipliziert dessen Einträge 1 geteilt durch die Anzahl der Spalten (also der Nutzer) sind. Die Matrix wird dann wieder mit dem Ergebnis Vektor multipliziert. Das wird n mal mit \(\lim_{n \to \infty}\) gemacht, bzw. bis keine Änderungen mehr auftreten, um heraus zu finden gegen welchen Wert die Einträge konvergieren (siehe Beispiel in Abb.1). Daher wird der PageRank auch davon beeinflusst, ob ein Nutzer von anderen Nutzern verlinkt wird, auf die es selber viele Links gibt und somit einen höheren Stellenwert haben. Ein Nutzer hat also einen hohen PageRank, wenn er entweder viele niedrige PageRanks oder weniger sehr hohe bekommt.

Abb. 1

Bei diesem Algorithmus ist es so, dass wenn bspw. Nutzer A auf Nutzer B verlinkt und Nutzer B auf Nutzer C, dann bekommt Nutzer C einen höheren PageRank als Nutzer B, weil Nutzer C sogar eine Frage von jemandem beantworten konnte, der selber Fragen von anderen beantwortet und somit selber Expertise hat. Das Problem dabei besteht darin, dass es in bspw. einem Forum zum Thema Programmierung es verschiedene Bereiche gibt, zu denen Fragen gestellt werden können, wie unterschiedliche Programmiersprachen. Wenn Nutzer C also Fragen zur Programmiersprache Java beantworten kann, und B Fragen zu Python, heißt das nicht, dass C eine höhere Expertise hat als B, wie der PageRank Algorithmus aussagen würde, Nutzer B und C haben nur unterschiedliche Expertise.

Daher ist der PageRank Algorithmus nicht gut geeignet für Foren, bei denen es um verschiedene Themen geht. Wenn ein Forum nur ein spezifisches Thema behandelt ist liefert der Algorithmus sinnvolle Ergebnisse.

HITS

Der HITS (hypertext-induced topic selection) Algorithmus oder auch Hubs und Authorities berechnet für jeden Nutzer im Gegensatz zum PageRank Algorithmus zwei Werte. Es wird ein Hub Wert und ein Authority Wert berechnet, dabei ist das Vorgehen ähnlich wie beim PageRank Algorithmus iterativ. Ein guter Hub ist dabei ein Nutzer, der auf gute Authorities zeigt, und ein guter Authority ist ein Nutzer, der von guten Hubs aufgezeigt wird. In Foren können also Fragensteller gute Hubs und Antwortende gute Authorities sein.

Alle Nutzer Starten mit einem Hub und Authority Wert von 1. Der neue Hub Wert eines Nutzers A wird berechnet, indem der alte Authority Wert von allen Nutzern addiert wird, auf die der Nutzer A verweist. Der neue Authority Wert von Nutzer A wird dann berechnet, indem die alten Hub Werte der Nutzer addiert werden, auf die Nutzer A zeigt. Nach jeder Iteration werden alle Werte normiert, damit sie nicht immer weiter ansteigen. Bei der Normierung werden alle Authoritie/Hub Werte einer Iteration aufaddiert und dann wird jeder Authoritie/Hub Wert durch die Summe dividiert. Nach n Iterationen, für n geht gegen $\infty$, konvergieren die Werte dann wieder gegen den endgültigen Authority und Hub Wert eines Nutzers. Warum der HITS Algorithmus aber auch nicht optimal zur Expertenfindung geeignet ist, erkennt man an folgendem Beispiel in Abb. 2.

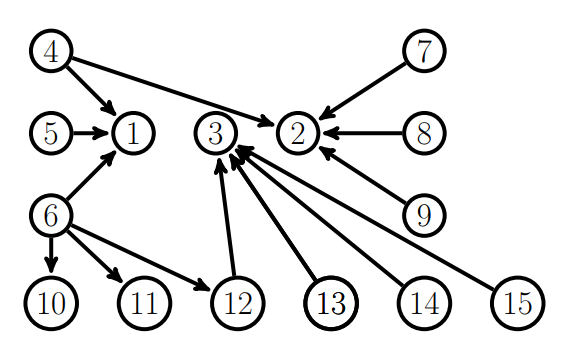
Abb. 2

In diesem Beispiel müssten die Nutzer 1,2 und 3 die mit den höchsten Authority Werten sein, da sie von vielen Nutzern verlinkt werden. Allerdings haben nach der Anwendung des HITS Algorithmus die Nutzer 1,2,10,11 und 12 hohe Authority Werte wohingegen der Nutzer 3 einen sehr geringen Authority Wert hat.

Dieses Ergebnis kommt daher, dass bei dem HITS Algorithmus generell der Einfluss der Hub Werten zu groß ist. Der Nutzer 6 seinen Hub Wert dadurch erhöht, dass er auf 1 verlinkt, was einen hohen Authority Wert hat. So bekommt auch Nutzer 4 einen etwas höheren Hub Wert und steigert dann durch das verlinken auf Nutzer zwei dessen Authority Wert. Die Nutzer 10, 11 und 12 haben ihren hohen Authority Wert ebenfalls dadurch, dass Nutzer 6 mit seinem sehr hohen Hub Wert auf sie verlinkt. Alle Nutzer die auf 3 verlinken haben einen eher geringen Hub Wert, weswegen auch der Authority Wert von Nutzer 3 gering bleibt. Auf Grund dieser Ergebnisse ist der HITS Algorithmus also zur Expertenfindung in Frage- und Antwort-Foren ungeeignet.

InDegree

Im Allgemeinen ist die Funktionsweise des InDegree Algorithmus ähnlich zu der des PageRank Algorithmus. Es werden die eingehenden Verlinkungen gezählt, was dann InDegree genannt wird. Der Ansatz ist also, die Nutzer nach ihrem InDegree zu sortieren und dann die ersten K Nutzer als Experten zu bestimmen.

Daher brauchen wir aber noch eine automatische Rechnung, die ein passendes K bestimmt. Zuerst definieren wir die \(N\)-elementige Menge \(X\) = {\(x_1\), \(x_2\), …, \(x_N\)}, die alle Nutzer enthält, welche mindestens einmal als beste Antwort angegeben, also verlinkt wurden.

\(y_i\) soll dann der InDegree von dem jeweiligen Nutzer \(x_i\) sein. Diese InDegree Werte müssen allerdings noch normiert werden. Dazu wird folgende Formel genutzt \(\sum_{i=1}^{N} (y_i)^2 = 1\).
Bei welchem Wert dann die Grenze K zwischen Experten und nicht Experten liegen sollte, betrachten als Beispiel ein Forum zum Thema “Engineering” aus Yahoo! Answers. Anhand der graphischen Darstellung der normierten InDegree Werte (Abb. 3) ist gut zu erkennen, wo die Grenze sinnvollerweise liegen sollte, nämlich bei 0.04. Der Graph wir also in zwei Komponenten aufgeteilt, wobei die eine im Bereich \(y_i\) < 0.04 liegt und die andere im Bereich 0.04 < \(y_i\) < 0.2. In dem zuerst genannten Bereich liegen dann alle Nutzer die keine Experten sind und im zweiten Bereich liegen alle Nutzer, die als Experte gesehen werden können.

Abb. 3 aus (Bouguessa et al., 2008)

Das Bestimmen der Grenze und somit das Einteilen in Bereiche sollte allerdings automatisch passieren und nicht durch Ablesen. Dafür können wir eine Wahrscheinlichkeitsdichtefunktion verwenden, die die Werte in zwei Partitionen teilt.

Laut dem Paper (Bouguessa et al., 2008)ist es sinnvoll anzunehmen, dass die normierten InDegree Werte durch eine Mischung von zwei Gamma Verteilungen modelliert werden können. Um dann die Experten von nicht Experten zu unterscheiden wird in dem Paper (Bouguessa et al., 2008) die genaue Wahrscheinlichkeitsdichtefunktion vorgestellt, die aus dem FCM und EM Algorithmus besteht.
Von den Ergebnissen, des EM Algorithmus kann dann abgeleitet werden, welche Nutzer Experten sind und welche nicht.

Beim InDegree Algorithmus sind die Ergebnisse am exaktesten verglichen mit den zwei oben beschriebenen Algorithmen. Das liegt daran, dass keine wichtigen Informationen vernachlässigt werden, wie beim PageRank Algorithmus. Es werden auch keine Annahmen getätigt, die zu falschen Ergebnissen führen, wie beim HITS Algorithmus die Annahme, dass Nutzer mit einem hohen Hub Wert einen sehr großen Einfluss auf den Authority Wert der verlinkten Nutzer haben.

Disassortative Degree Mixing and Information Diffusion (DMID)

„Disassortative degree mixing“ ist die Eigenschaft mancher sozialer Netzwerke, dass höchstbewertete Knoten öfter Verbindungen zu niedrigstbewerteten Knoten haben. Knoten, in diesem Kontext, sind Nutzer und die Verbindungen werden durch Beiträge zu denselben Themen definiert. Der Algorithmus hat zwei Phasen – in der ersten wird die Eigenschaft des Dissoziative Degree Mixing in Kombination mit den dadurch erzeugten Graden/Bewertungen der Knoten dafür benutzt, um Authoritätspersonen einer Community, die sogenannte „Leader“ oder Anführer zu finden.

Im zweiten Schritt wird der Kontaktgrad von anderen Knoten zu den Leadern berechnet. Hierbei kommt es zu Überlappungen, die dann darauf schließen lassen, wie nah verwandt einzelne Communities zueinander sind.

Speaker Listener label Propagation Algorithm (SLPA)

Der zweite OCD-Algorithmus ist SLPA. Mit ihm ist das Ziel, Knoten in die Kategorien „Zuhörer“ und „Sprecher“ einzuteilen. Dies ist eine Form der Einteilung, die tatsächlichem Menschlichen Verhalten näherkommt. Sprecher stellen Informationen bereit, während Zuhörer diese Informationen nutzen.

Der iterative Algorithmus initialisiert zuerst jeden Knoten mit einem unbestimmten Label. Dann wählt er einen Knoten als Zuhörer und analysiert seine Nachbarn (also alle Knoten, die eine direkte Verbindung zu ihm haben). Basierend auf voreingestellten Sprecher-Richtlinien senden alle Nachbaren jeweils ein bestimmtes Label. Zum Beispiel können diese Sprecher-Richtlinien Regeln besagen, dass die Auswahl der Label dem Prinzip des gewichteten Zufalls folgt. Die Gewichtung, in diesem Fall, basiert auf der Frequenz des Vorkommens der Label.

Daraufhin nimmt der Zuhörerknoten die Label basierend auf seinen Zuhörer-Richtlinien an. Diese enthalten wiederum Regeln wie zum Beispiel das Akzeptieren des beliebtesten Labels.

Durch verschiedene Sprecher- und Zuhörer-Richtlinien kann man die Vererbung von Labeln beobachten. Letztendlich werden alle Label zusammengenommen und dem Post-Processing unterzogen. Dadurch werden sie in eine Verteilung von Wahrscheinlichkeiten, dass ein Label auftritt, umgewandelt.

Der Vorteil von SLPA ist die schnelle Geschwindigkeit und zuverlässige Sensibilität.

Resultat

Wir können die Anwendungsfälle der Algorithmen in Frage- und Antwort-Foren in zwei Fälle einteilen. Den Fall eines Froums mit mehreren verschiedenen Themenbereichen und den Fall zu nur einem spezifischen Themenbereich.
Ein Beispiel für ein Forum mit nur einem Thema, wäre ein Forum nur zum Thema der Programmiersprache Java. Hier erzielt der Algorithmus InDegree gute Resultate, ebenso gute Resultate erreichen auch die OCD Algorithmen, auch wenn es sich um zwei grundlegend verschiedene Ansätze handelt.

Für den zweiten Fall wäre ein Beispiel Stackoverflow. Also ein Forum zu generellen Programmierkonzepten und der Programmierung mit verschiedenen Programmiersprachen. Hier ist InDegree nicht mehr anwendbar, da keine Unterscheidung zwischen den verschiedenen Unterthemen getroffen wird und die Ergebnisse dadurch verfälscht werden. Dahingegen funktionieren die OCD Algorithmen hier optimal, da diese darauf ausgelegt sind in solchen Netzwerken auch zwischen Commuities zu unterscheiden.

Damit sind OCD Algorithmen zur Expertenfindung in Frage- und Antwort-Foren insgesamt zu bevorzugen.

Diskussion

Schwächen unserer Methoden

Dieses Paper entstand im Kontext eines Proseminars, deshalb sieht der Umfang keine eigene Forschung oder umfangreiche Testung vor. In unseren Methoden waren wir somit auf den Vergleich und die Diskussion bereits existierender Ressourcen beschränkt. Außerdem ist es schwierig eine „allgemeine“ Empfehlung zu stellen, da alle vorgestellten Algorithmen für ihre eigenen, spezifischen Use-Cases entwickelt wurden. Somit kann es immer sein, dass Algorithmen, die wir als weniger effektiv ansehen, in bestimmten Situationen bessere Resultate liefern. Somit sollte der Wahl eines Expertenfindungs-Algorithmus immer eine gründliche Analyse des Zieles vorangestellt werden.

Wo besteht noch Forschungsbedarf?

Genauso wie sich die gesamte Kategorie der OCD-Algorithmen im Vergleich mit „normalen“ Algorithmen als effektiver herausgestellt hat, ist es nicht ausgeschlossen, dass eine bisher unbekannte neue Kategorie an Algorithmen deutlich effektiver als OCDAs ist. Somit besteht Forschungsbedarf im Bereich der Suche nach diesen effektiveren Algorithmen.

Schlussfolgerung (Conclusion)

Nach unserer Betrachtung der verschiedenen Algorithmen zur Expertenfindung kamen wir zu dem Schluss, dass es zwar spezifische Anwendungsgebiete gibt, in dem der Indegree-Algorithmus den OCD-Algorithmen in nichts nachsteht, jedoch ist die Verwendung von letzeren selbst in solchen Fällen zu bevorzugen. Insgesamt schließen wir also auf die Empfehlung von OCDAs für die Expertenfindung.

Referenzen

1. Bouguessa, M., Dumoulin, B., & Wang, S. (2008). Identifying Authoritative Actors in Question-answering Forums: The Case of Yahoo! Answers. Proceedings of the 14th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD’08), 866–874. https://doi.org/10.1145/1401890.1401994
2. Shahriari, M., Parekodi, S., & Klamma, R. (2015). Community-aware Ranking Algorithms for Expert Identification in Question-answer Forums. Proceedings of the 15th International Conference on Knowledge Technologies and Data-Driven Business, 1–8. https://doi.org/10.1145/2809563.2809592