Erweiterung OCDA auf vorzeichenbehaftete Netzwerke (3)
| Laurenz Haug | Simon Hebich | ||
|---|---|---|---|
| RWTH Aachen University | RWTH Aachen University | ||
| laurenz.haug@rwth-aachen.de | simon.hebich@rwth-aachen.de |
Abstract
In der modernen Gesellschaft sind soziale Netzwerke mittlerweile unabdingbar. Vor allem während einer globalen Pandemie hat sich das Kennenlernen zwischen mehreren Personen und Personengruppen zu großen Teilen in das Internet ausgelagert. Das gibt Wissenschaftler*Innen die Möglichkeit auf wesentlich mehr Daten zurückzugreifen, sodass es ihnen besser gelingt soziale Communities zu entdecken. Definiert ist eine Community als eine Gruppe von Personen, welche gleichen Interessen teilen und sich daher miteinander assoziieren. Dies hilft den Wissenschaftler*Innen besser zu verstehen wie sich Communities bilden und vorherzusagen, wie diese sich in näherer Zukunft verändern und entwickeln werden.
Analysiert werden hierbei synthetische oder aus realen Daten generierte soziale Netze, in denen einzelne Nodes im Gegensatz zu vergangen Ansätzen mehreren Communities angehören können. Dies wird durch Overlapping Community Detection Algorithms (OCDA) realisiert, die aktuell oft auf Netze mit ausschließlich positiv gewichteten Links angewendet werden. Dies ist jedoch nicht der effizienteste Ansatz. Im Folgenden wird erläutert wie die Erweiterung von Verbindungen durch eine negative Gewichtung vorteilhaft für die Effizienz von OCDAs und der Evaluation von Links in sozialen Netzwerken sind. Dieser Ansatz verspricht in praktischen Anwendungen bisher bestehende Algorithmen in Geschwindigkeit und Genauigkeit zu übertreffen.
Inhaltsverzeichnis
1 Einleitung
Netzwerke bestehen aus Entitäten verschiedener Art und dessen Beziehungen zueinander. Sie umgeben den modernen Menschen täglich und zu jeder Uhrzeit. Diese zu modellieren und analysieren hat in den letzten Jahren an Beliebtheit sehr stark zugenommen. Sowohl biologische Prozesse, politische Beziehungen zwischen Ländern als auch soziale Zusammenhänge zwischen verschiedenen Menschen und Menschengruppen lassen sich als Graphen modellieren. Letzteres wurde jedoch mit der Erfindung des Internet um ein Vielfaches wissenschaftlich lukrativer, da zur heutigen Zeit Mengen an Rohdaten zur Verfügung stehen die vor einigen Jahren noch unvorstellbar waren. Speziell in der Analyse von Daten von Social Media Plattformen sind Algorithmen zur Entdeckung von Gemeinschaften mittlerweile unverzichtbar. Diese Algorithmen werden auch Overlapping Community Detection Algorithmus (OCDA) genannt. Bei diesen Algorithmen werden die Benutzer Gruppen, sogenannte Communities, zugeordnet die sich ein bestimmtes Attribut teilen. Jeder Benutzer kann zu vielen Communities gehören wodurch es zu starken Überschneidungen von Communities (Overlapping Communities) kommen kann. Diese Überlappung kann viel Aufschluss über den Aufbau und die Dynamik der einzelnen Benutzer und Benutzergruppen geben die für die jeweiligen Plattformen sehr relevant sind.
Um die gesammelten Rohdaten mit OCDAs erforschen zu können werden diese meist in mathematische Graphen umgewandelt. Ein solcher Graph \(G\) besteht aus Knoten \(V\) die die Benutzer in dem sozialen Netzwerk darstellen. Die Verbindungen zwischen diesen werden von Kanten \(E\) dargestellt.
Die Kanten zwischen den Koten können gewichtet werden. Ein höheres Gewicht bedeutet eine stärkere Bindung. In Vergangenheit wurden hier ausschließlich positive Gewichte zur Modellierung von Relationen verwendet. Es ist jedoch möglich auch negative Gewichte zur Darstellung von Feindschaften zu nutzen. Diese Graphen werden dann als vorzeichenbehaftet beschrieben.
Es gibt bereits viele Datensätze die negativen Kanten benutzen jedoch können auch bestehende soziale Graphen in vorzeichenbehaftete soziale Graphen umgewandelt werden, indem ab einem bestimmten Mittelwert alle Gewichte über diesem Wert in positive und alle darunter in negative Kanten verwandelt werden.
Viele Algorithmen zur Analyse von ausschließlich positiv gewichteten sozialen Graphen sind mittlerweile bekannt und werden vielseitig verwendet. Außerdem wurde an ihnen schon viel geforscht, um dieser Effizienter und somit schneller zu machen. Diese Algorithmen können jedoch nicht für vorzeichenbehaftete soziale Graphen verwendet werden. Einen solchen Algorithmus zu entwickeln, dauert viel Zeit und Ressourcen weshalb eine weitere Möglichkeit ist bestehende effiziente Algorithmen so zu erweitern, dass sie auch auf vorzeichenbehafteten Graphen funktionieren. Im Folgenden wird ein sehr bekannter Graph Algorithmus so modifiziert, sodass er auch negative Kanten mit auswerten kann.
2 Verwandte Arbeiten
Ein weiterer häufig verwendeter Algorithmus zumr Entdeckung von Gemeinschaften in sozialen Netzen ist der Girvan-Newman-Algorithmus (Girvan & Newman, 2002). Dieser Algorithmus identifiziert Kanten in einem Netzwerk, die zwischen Gemeinschaften liegen, und entfernt sie dann, so dass nur die Gemeinschaften selbst übrig bleiben. Die Laufzeit dieses Algorithmus beträgt \(O(|V|^2 \cdot |E|)\) und ist somit nicht geeignet für große Datenmengen.
3 Methodik
3.1 Breadth first search
Die erste Phase des Algorithmus nutzt Breadth first search (Bfs) (Cormen et al., 2007, cop. 2001).
Dieser Algorithmus durchsucht einen gegebenen Graphen immer in Einzel Schritten.
Am Anfang werden alle Knoten mit der Farbe Weiß, mit dem Wert “unendlich” und mit leerem Vater initialisiert. Die Farbe symbolisiert, dass der Knoten noch nicht von Bfs entdeckt wurde, der Wert in dem jetzt gerade noch “unendlich” steht gibt an nach wie vielen Schritten der Knoten vom Bfs entdeckt wird und der Vater Knoten zeigt an wo der Bfs Algorithmus vorher im Graphen war. Nun beginnt der Algorithmus bei einem zufälligen Punkt oder gegeben Punkt und schaut sich von diesem alle möglichen Knoten an, die mit ihm Benachbart sind. Dieser Knoten wird mit Wert 0 und der Farbe Grau initialisiert, diesen Knoten nennt man dann Startknoten. Die Farbe Grau signalisiert, das der Knoten vom Algorithmus entdeckt wurde. Alle vom ihm benachbarten Knoten werden nun auch entdeckten und daher auch grau markiert. Entdeckte Knoten werden in eine FiFo-Queue gelegt, um später zu wissen in welcher Reihenfolge man die Konten abarbeiten muss.
Die Entdeckungszeit von jedem Knoten beträgt k+1, wobei k für den Wert des jeweiligen Vaterknotens steht. Wenn von einem Knoten alle seine benachbarten Knoten grau, sprich entdeckt sind, wird dieser Knoten schwarz. Wenn ein Knoten schwarz ist, signalisiert dies, dass der Knoten fertig bearbeitet ist und der Algorithmus sich nun den nächsten Knoten anschauen kann.
Der nächste Knoten, der dann folgt, ist das erste Element aus der FiFo-Queue. und wiederhohlen den Prozess auf diesen Knoten. Auch hier werden wieder Elemente in die Queue gelegt, aber nur wenn dieses Element noch weiß war, sprich unentdeckt war. Somit wird verhindert das der Algorithmus nicht wieder Knoten untersucht, die er vorher schon einmal untersucht hatte. Dies wird so lange gemacht bis Bfs die Queue komplett abgearbeitet hat und alle Elemente in dem Graphen schwarz sind.
for each knoten u in G.V // Geht jede Kanten im Graphen durch
u.color = weiss
u.d = unendlich
u.vater = none
s.color = grau
s.d = 0
s.vater = none
Q = empty // Initalisierung der FiFo-Queue
Enqueue(Q,s)
while Q != empty
u = Dequeue(Q)
for each v in G.nachbar(u) //sucht alle Nachbarn des Knotens u raus
if v.color == weiss
v.color = grau
v.d = u.d+1
v.vater = u
Enqueue(Q,v) // Endeckte Knoten werden in der Queue getan
u.color = schwarz //u wurde verarbeitet und ist fertig
Bild 1: Pseudocode eines Bfs Algorithmus.
Ein Beispiel Lauf auf einen Graphen sähe wie folgt aus:
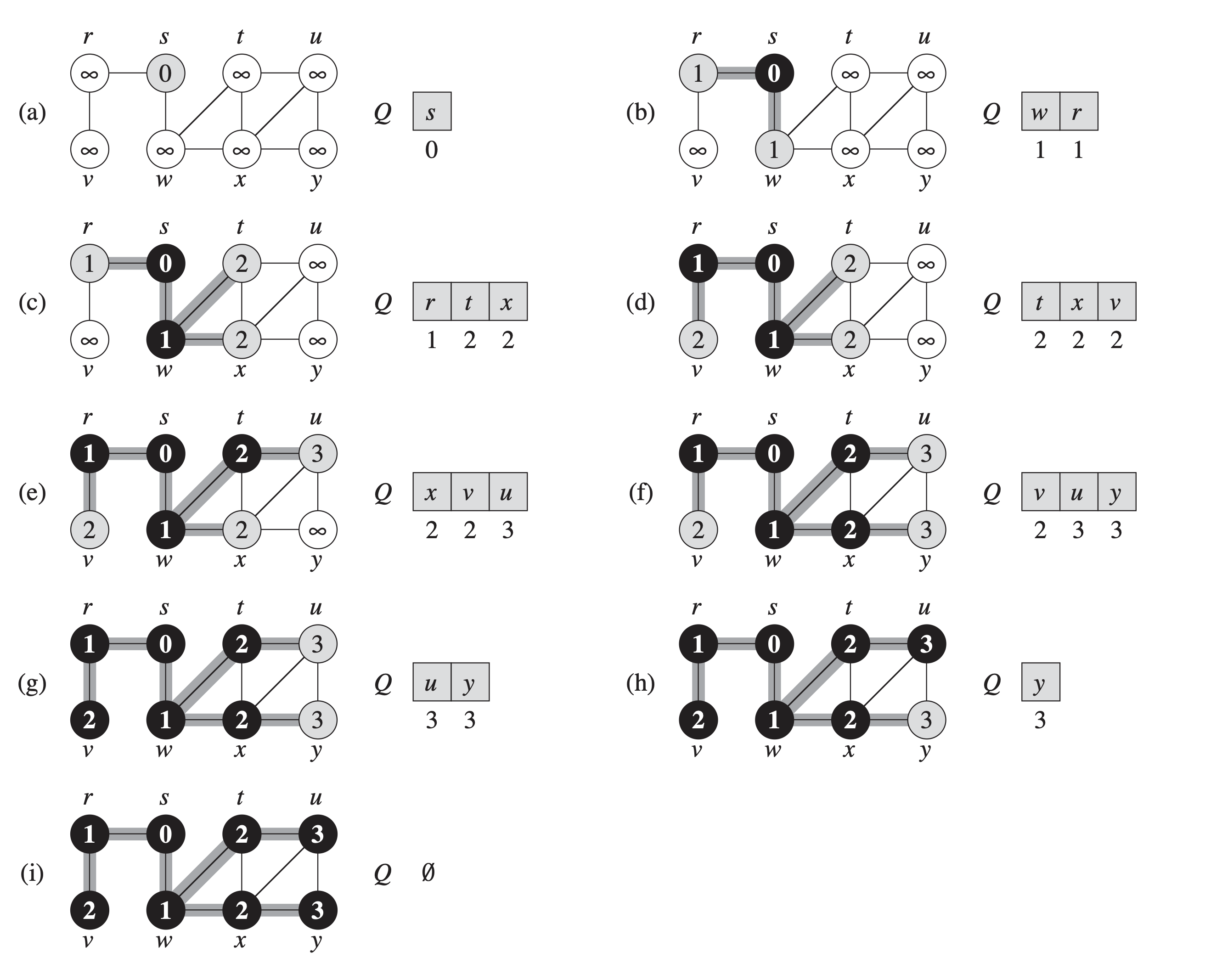 (Cormen et al., 2007, cop. 2001)
(Cormen et al., 2007, cop. 2001)
3.2 Breadth First Clustering
Für die Ausführung des Breadth First Clustering (BFC) Algorithmus (Bhatia & Gaur, 102008) werde einige Variablen benötigt, die im Folgenden erläutert werden. Dieser gehört zu der Klasse der OCDAs und gibt einen gruppierten Graphen zurück.
Für jeden Knoten \(v \in V\)
VC ← Besucherzahl
AV ← Anzahl der direkt mit \(v\) verbundenen Knoten.
NCV ← Anzahl an noch nicht gruppierten mit \(v\) verbundenen Knoten, mit einer Besucherzahl ≥ 2
CV ← Anzahl an gruppierten mit \(v\) verbundenen Knoten, mit einer Besucherzahl ≥ 2
MPC ← Gruppe mit den meisten benachbarten Knoten von \(v\)
Zusätzlich wird bei jedem Schritt geschaut, ob die Besucherzahl das Knoten größer als 2 ist, wenn dies der Fall ist, existiert eine Gruppe, zu der dieser Knoten gehört.
Größere Gruppierungen entstehen dann, wenn sich mehrere kleinere Gruppen zu einer größeren vereinigen.
Wenn ein Knoten nun zu zwei Gruppen zugehörig ist, gibt es eine Fallunterscheidung anhand welcher ermittelt wird wie man mit dem Knoten umzugehen hat.
Case 1: AV/2 > (NCV+CV)
Case 2: NCV > CV // nur wenn Fall eins falsch ist
Case 3: CV > NCV // nur wenn Fall eins falsch ist
Case 1 betrifft den Fall, das die Anzahl der Nachbar Knoten, mit Besucherzahl von eins oder kleiner, mehr sind als die Nachbar Knoten mit Besucherzahl zwei oder größer.
Wenn die Anzahl der Knoten, die bereits gruppiert wurden, kleiner ist als die Anzahl der noch nicht gruppierten Knoten, mit Besucherzahl zwei oder größer, tritt Case 2 auf. In diesem Case wird dann eine Neue Class erstellt in die der aktuelle Knoten sowie seine noch nicht gruppierten Nachbarn gespeichert werden.
Der Case 3 tritt ein, wenn die Anzahl der gruppierten Knoten größer ist als die Anzahl an ungruppierten Knoten. Wenn dieser Case auftritt, wird der MPC ermittelt und der aktuelle Knoten der Gruppe zugeordnet, in der er am meisten Nachbarn hat.
BFC(G,U)
begin 1
Enqueue(Q,U)
set U as besucht
while Q is not empty
begin 2
H = Dequeue(Q)
for each N in nachbarn(H)
begin 3
erhoehe Besucherzahl(N)
if Besucherzahl(N) == 0
begin 4
Enqueue(Q,N)
set N as besucht
end 4
if Besucherzahl(H)>1
begin 5
if(CV+NCV)> Ceiling(AV/2) // Case 1 wird gescheckt
begin 6
if NCV > CV // Case 2 wird gescheckt
begin 7
from S_ncv of NCV Knoten
set class(S_ncv) = C+1
end 7
else if CV > NCV // Case 3 wird gescheckt
begin 8
find MPC
set class(H) = MPC
end 8
end 6
end 5
end 3
end 2
For all Knoten left ungruppiert
put in MPC
end 1
- Bespiel Code für ein BFC
3.3 Clustering Reclustering Algorithm
Der Algorithmus(Sharma et al., n.d.) basiert in der ersten Phase auf dem BFC-Algorithmus und wird in einer zweiten Phase so erweitert, dass die negativen Kanten berücksichtigt werden.
Dabei werden die Knoten mit einer negativen Kante anhand ihres Teilnahmeniveau ggf. neu gruppiert. Die Berechnung des Teilnahmeniveaus VP erfolgt wie folgt:
\[VP = \frac{\text{Anz. der positiven Kanten in der akt. Gruppe}}{\text{Anz. aller Kanten in der akt. Gruppe}}\]Somit wird bei jedem der zuvor ausgesuchten Knoten das Teilnahmeniveau für jede Gruppe berechnet, in der ein direkter Nachbar des aktuellen Knoten ist. Der aktuelle Knoten wird nun der Gruppe/n mit dem höchsten Teilnahmeniveau zugeordnet.
Phase1
CG = Ergebnis aus BFC(G,U) // BFC wird ausgeführt und Ergebnis für Phase2 verwendet
Phase2(CG)
begin 1
fuer jede Gruppe C_i mit i={1,2, ..., n}
begin 2
finde alle Knoten V_i mit negativer Kante
ENQUEUE(V_i, Q2)
end 2
DEQUEUE(V_i, Q2)
begin 3
fuer jede Gruppe C_i
zaehle die Anzahl der positiven Kanten die in Gruppe C_i enden
sortiere die Gruppen nach voriger Zahl absteigend
end 3
begin 4
fuer jede verbundene Gruppe
brechne VP
end 4
finde Gruppe mit groesstem VP
falls die Guppe mit dem groesste VP nicht die Guppe des aktuellen Knoten ist
loesche Knoten aus der aktuellen Gruppe
weise Knoten der Gruppe mit dem groessten VP zu
end 1
4 Evaluation
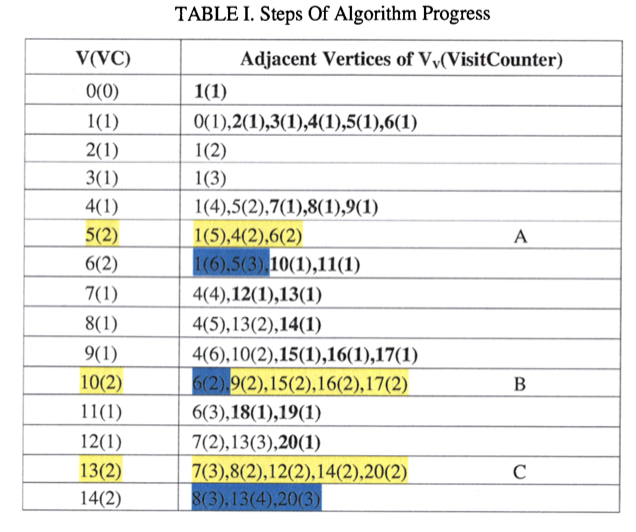
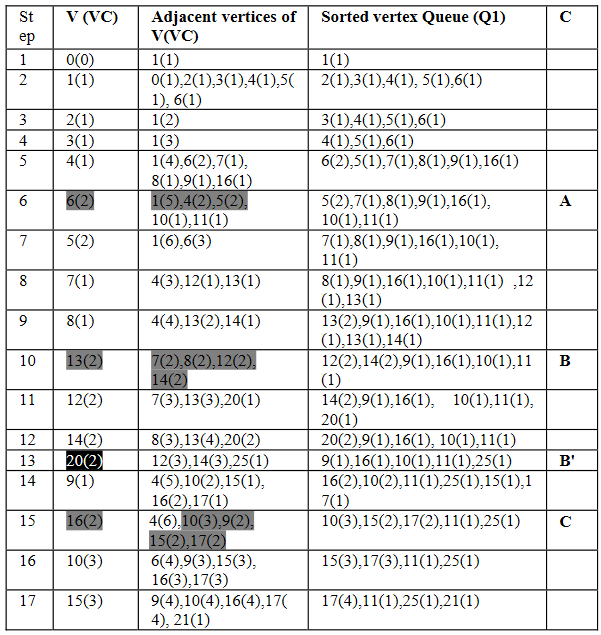
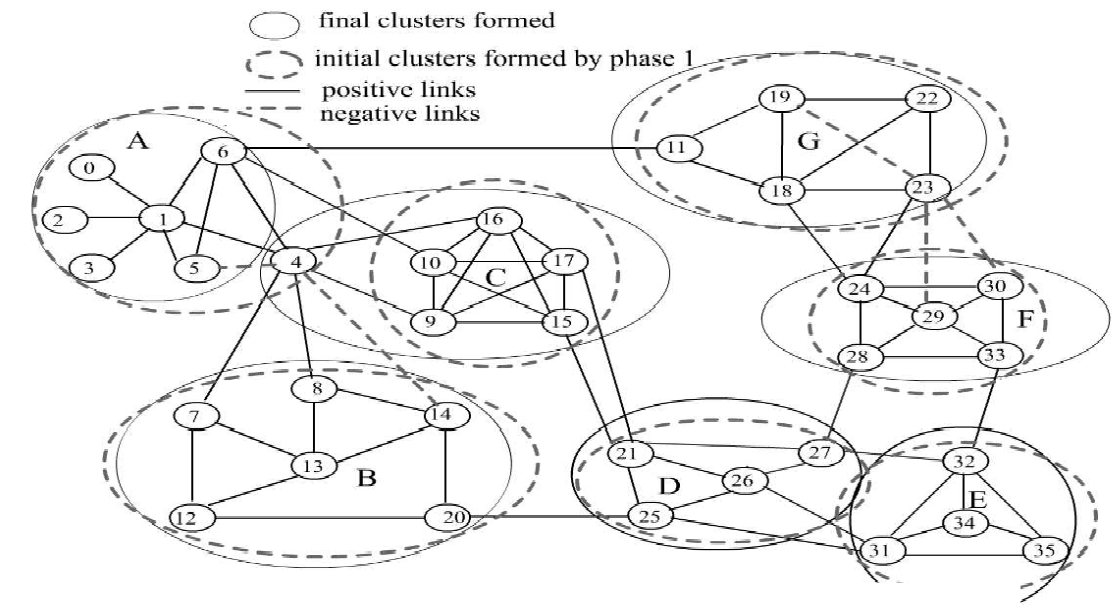
In Schritt sechs haben wir das erste Mal den Fall, dass der Knoten der als nächstes bearbeitet werden soll eine Besucherzahl von zwei oder größer hat. Somit werden alle benachbarten Knoten mit einer Besucherzahl größer gleich 2 zu einer Gruppe (A) vereinigt. Dies geschieht bei jedem Schritt, der in der Tabelle grau markiert ist.
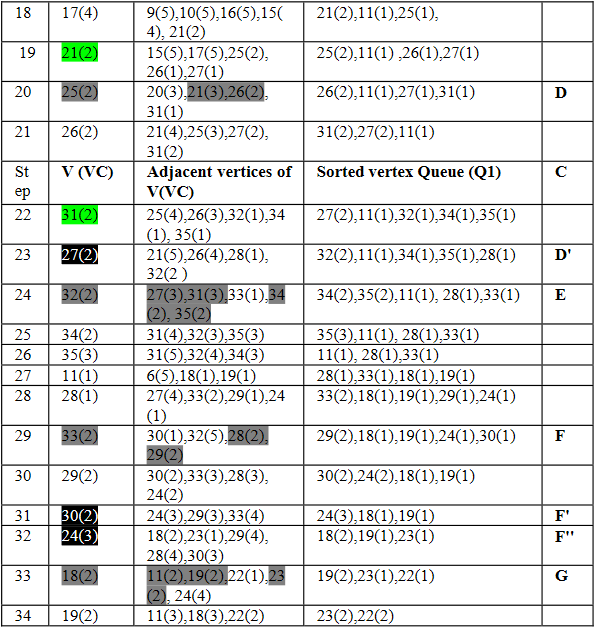
Bei schwarz markierten Schritten ist CV > NCV, somit wird der aktuelle Knoten seinem MPC zugeordnet. Ein Beispiel dafür ist Schritt 13 in dem der Knoten 20 der Gruppe B hinzugefügt wird, da die Mehrzahl seiner benachbarten Knoten bereits geclustert sind und diese beide in Gruppe B sind (MPC).
Bei allen grün markierten Knoten in der Tabelle ist Case 1 nicht gegeben somit bleiben diese Knoten unguppiert. Theoretisch müssten diese Knoten nach dem Algorithmus dann ihrem MPC zugeordnet werden, jedoch wird der Teil im Code, in dem das MPC berechnet wird, übersprungen, sodass es kein MPC gibt dem der Knoten zugeordnet werden kann.
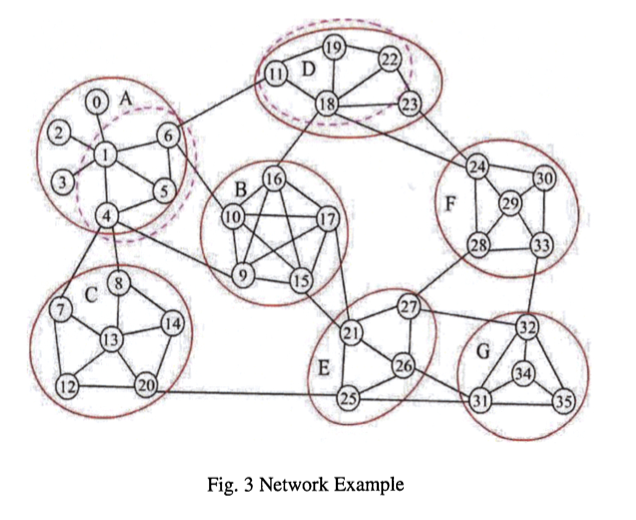
In Phase 2 werden nun von allen Knoten, die über eine negative Kante zu einem andern Knoten verfügen der VP berechnet. Diese Knoten sind in unserem Beispiel die Knoten: 4,5,14,19,23,29,30. Anschließend wird der Betrachtete Knoten nun der Gruppe/n (neu) zugeordnet die das größte VP besitzen.
Beispielsweise hat Knoten 4 insgesamt 3 Verbindungen in Gruppen A und B, sowie 2 in C. In C sind beide dieser Verbindungen positiv und somit folgt VP = 1. Zu A und B hat Knoten 4 jeweils eine negative Kante was bei der VP-Berechnung zu einem Wert von jeweils 2/3 führt. Da 2/3 < 1 wird 4 der Gruppe C zugeordnet.
Die Laufzeit des CRA ist linear und somit im Gegensatz zum Girvan-Newman-Algorithmus für größere Datenmengen besser geeignet.
5 Zusammenfassung
Dieses Paper erläutert die Grundlagen der Analyse von sozialen Netzen und zeigt einen möglichen Algorithmus, um dies zu tun. Somit haben wir einen Algorithmus vorgestellt der schnell und ohne großen Aufwand auch auf größeren Datensätzen funktionieren kann. Das besondere hierbei ist, dass dieser Algorithmus anders als die in der Einleitung erwähnten auch negative Kanten berücksichtigt. In Zukunft könnte der erläuterte CRA Algorithmus so erweitert werden, sodass er Kantengewichte \(\in Q\) berücksichtigen kann.
Referenzen
- Girvan, M., & Newman, M. E. J. (2002). Community structure in social and biological networks. Proceedings of the National Academy of Sciences, 99(12), 7821–7826. https://doi.org/10.1073/pnas.122653799
- Cormen, T. H., Leiserson, C. E., Rivest, R. L., & Stein, C. (2007, cop. 2001). Introduction to algorithms (2nd. ed., 10th printing). MIT Press and McGraw-Hill.
- Bhatia, M. P. S., & Gaur, P. (102008). Statistical approach for community mining in social networks. 2008 IEEE International Conference on Service Operations and Logistics, and Informatics, 207–211. https://doi.org/10.1109/SOLI.2008.4686392
- Sharma, T., Charls, A., & Singh, P. K. Community Mining in Signed Social Networks - An Automated Approach. 2009 International Conference on Computer Engineering and Applications, 2, 152–157. http://www.ipcsit.com/vol2/28-A217.pdf