Mathematische Grundlagen
| Henri Nagel |
|---|
| RWTH Aachen University |
| henri.nagel@rwth-aachen-de |
| Jessica Pelz |
|---|
| RWTH Aachen University |
| jessica.pelz@rwth-aachen.de |
| David Brenn |
|---|
| RWTH Aachen University |
| david.brenn@rwth-aachen.de |
Lineare Algebra: Vektoren
n-Dimensionaler Vekor:
\(\begin{bmatrix}
x_{1} \\
x_{2} \\
\vdots \\
x_{n}
\end{bmatrix} = \begin{bmatrix}
x_{1}& x_{2} & \cdots & x_{n} \
\end{bmatrix}\)
Einheitsvektor: Jeder Vektor mir der Länge 1
\[\begin{Vmatrix}[r] v \end{Vmatrix} = \sqrt[2]{v^T v} = 1\]Skalarprodukt: Gegeben seien zwei Vektoren \(v = (x_{1},x_{2},x_{3},...,x_{n})\) und \(w = (y_{1}, y_{2}, y_{3},...,y_{n}),\) dann gilt:
\[v,w = x_{1}y_{1} + x_{2}y_{2} + ... + x_{n}y_{n}\]ist das Skalarprodukt der beiden Vektoren.
Lineare Algebra: Matrizen
Transponierte Matrizen:
\[A =\left[\begin{array}{rrr} a_{11} & \cdots & a_{1n} \\ \vdots & \ddots &\vdots \\ a_{m1} & \cdots & a_{mn} \\ \end{array} \right] A^T =\left[\begin{array}{rrr} a_{11} & \cdots & a_{m1} \\ \vdots & \ddots &\vdots \\ a_{1n} & \cdots & a_{mn} \\ \end{array} \right]\]Symmetrische Matrizen: \(A^T = A\)
Inverse (quadratische) Matrizen: \(A^{−1} \text{ mit } AA^{−1} = A^{−1}A = I\)
Singuläre Matrix: Es existiert keine inverse Matrix zu \(A\)
Netzwerke: Definition eines Netzwerks
Netzwerk \(G = (V, E)\), mit:
\(V = {v1, v2, ..., vn}\) eine (endliche) Menge von Knoten,
\(E \subseteq V \times V\) eine (endliche) Menge Kanten.
Nachbarn: Zwei Knoten, welche mit einer Kante verbunden.
Gerichtetes Netzwerk: Eine gerichtete Kante ist ein geordnetes Knotenpaar \((u, v)\).
\(u\) und \(v\) werden Startknoten und Endknoten genannt.
Ungerichtetes Netzwerk: Die Kanten \((u, v)\) und \((v, u)\) sind identisch.
Gewichtetes Netzwerk: Funktion \(w ∶ E \rightarrow R\) ordnet jeder Kante \(e \in E\) einen Wert \(w\) zu.
Weitere Definitionen
Grad eines Knoten \(deg(v_i)\): Anzahl der eingehenden und ausgehenden Kanten.
In einem gerichteten Graphen gilt: \(deg^+(v_i)\) und \(deg^−(v_i)\) bezeichnen die ein- und ausgehenden Kanten.
Ein Pfad ist eine Sequenz von Knoten \(v_1, . . . , v_n\)
mit \((v_i, v_{i+1}) \in E, \text{ für } 1 \leq i < n.\)
Länge eines Pfades: Anzahl der Kanten eines Pfads.
Ein Pfad ist ein einfacher Pfad, wenn alle Knoten des Pfades paarweise verschieden sind.
Ein zyklischer Pfad ist ein Pfad mit \(v_1 = v_n\) und Länge \(m \geq 1\).
Ein Unter-Netzwerk eines Netzwerks \(G = (V, E)\) ist ein Netzwerk \(G' = (V', E')\) mit \(V' \subseteq V\) und \(E' \subseteq E\)
Vollständiges Netzwerk: Es existiert eine Verbindung zwischen jedem Knotenpaar.
Reguläres Netzwerk: Jeder Knoten hat den gleichen Grad. Ein Netzwerk heißt \(r\)-regulär, wenn dieser Grad \(r\) ist.
Adjazenz Matrix
Eine \(n \times n\)-dimensionale Matrix \(A\) mit \(a_{ij} = \left\{ \begin{array}{rr} 1 & \text{wenn }(v_i, v_j) \in E \\ 0 & \text{sonst} \\ \end{array} \right.\)
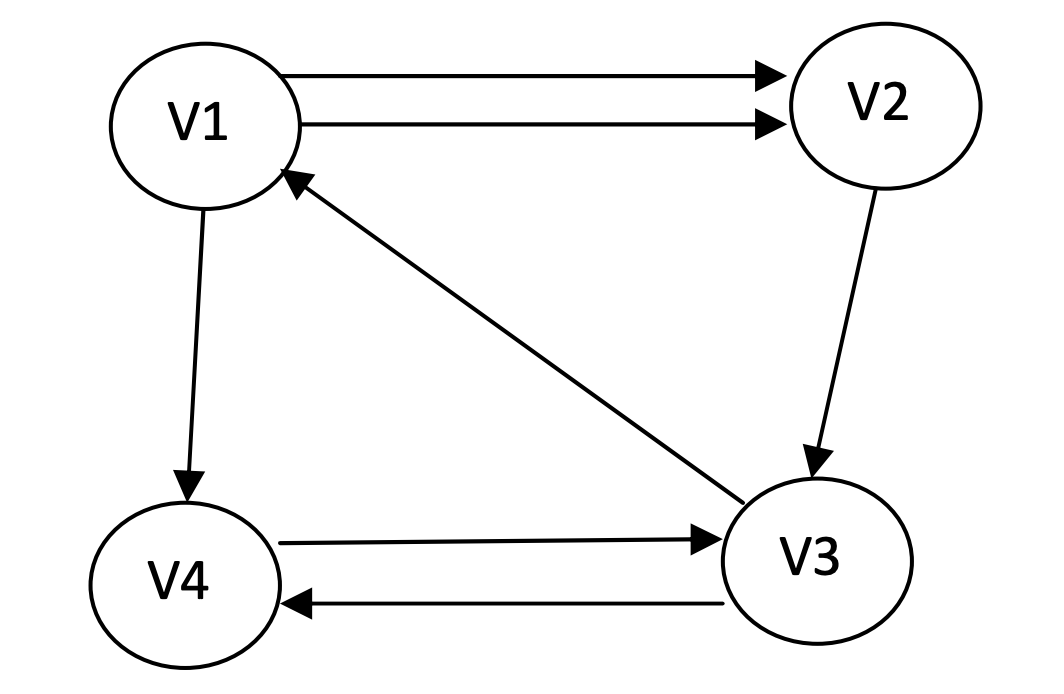
Beispiel:
\(A =\left[ \begin{array}{rrrr}
0 &1 &0 &1 \\
0 &0 &1 &0 \\
1 &0 &0 &1 \\
0 &0 &1 &0 \\
\end{array}\right]\)
Multi-Layer Netzwerk
Repräsentation einer komplexeren (mehrschichtigen) Struktur als Netzwerk
ML Netzwerk \(M = (V_M,E_M,V,L)\), mit:
- \(V = \{v_1,v_2,\ldots, v_n\}\) eine (endliche) Menge von Knoten
- \(L = \{L_a\}^{d}_{a=1}\) eine Menge von Layers für jeden Aspekt \(a\) (Aspekte sind z.B. Interaktion, Zeit usw.)
- \(V_M \subseteq V \times L_1 \times \ldots \times L_d\) Kartesisches Produkt von Konten und Layers
- z.B. \((u, \alpha_1, \ldots, \alpha_d)\) bedeutete dass Knoten \(u\) Teil von Layers \(\alpha_1,\ldots, \alpha_d\) ist
- \(E_m \subset V_m\times V_m\) eine (endlich) Menge Kanten
- Im ML Netzwerken müssen wir die Layers der Nachbarknoten angeben (\(V_m\) statt \(V\))
Beispiel für Multi-Layer Netzwerk
Bsp.: \(V = 1,2,3,4 \:\:\: L_1 = \{A,B\}, L_2=\{X,Y\}\)
Es gibt in diesem Fall 4 verschiedene Layers: \((A, X), (A, Y), (B, X), (B, Y)\)
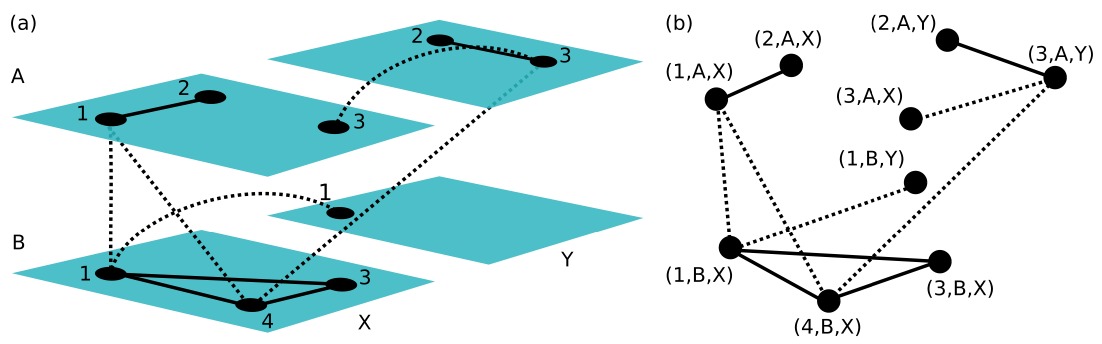
Abbildung: http://arxiv.org/pdf/1309.7233